Задачи, которые не успели написать, разберу кратко. Задавайте вопросы.
Идея: Gerald Реализация: tunyash Разбор: fdoer
Эту задачу можно было решать разными способами, например, таким: рассмотрим перестановку p, в которой pi = i, то есть просто последовательность чисел от 1 до n. Очевидно, для неё условие ppi = i выполняется всегда. Осталось только преобразовать её таким образом, чтобы выполнялось и второе условие: pi ≠ i. Для этого поменяем местами каждые два соседних элемента, т.е. для каждого k: k * 2 ≤ n поменяем местами значения p2k - 1 и p2k. Нетрудно убедиться, что для полученной перестановки оба условия выполняются всегда.
Идея: tunyash Реализация: tunyash, Gerald Разбор: fdoer
Для начала найдем диапазон значений, которые может принимать s(x). Так как из уравнения x2 ≤ n, а по условию n ≤ 1018, x ≤ 109, иначе говоря, десятичная запись любого решения не длиннее 10 цифр. Значит, максимальное значение smax = s(9999999999) = 10·9 = 90 (на самом деле это грубая оценка, smax даже меньше, но нам достаточно и её).
Переберем значение s(x): 0 ≤ s(x) ≤ 90. Получаем обычное квадратное уравнение относительно переменной x. Осталось решить его и проверить равенство того значения s(x), что мы зафиксировали, сумме цифр в разрядах полученного корня. Если корень нашелся и равенство выполнено, обновим ответ.
Пожалуй, самое важное в этой задаче — аккуратно и без ошибок вычислений считать дискриминант.
Подчеркну, что для решения задач div2.A и div2.B не требовалось знание массивов.
Идея: tunyash, fdoer Реализация: tunyash Разбор: tunyash
Будем добавлять ребра в порядке сортировки сначала по вершине в меньшим номером, затем с большим (просто два for'a). Если добавление ребра вызывает переполнение кол-ва циклов, не добавляем его. Считать количество циклов, которые добавятся можно за O(n) (могут появиться только циклы, содержащие добавленное ребро, следовательно достаточно перебрать третью вершину). Очевидно, что это найдет какой-то ответ, потому что, добавив два ребра из вершины мы всегда можем получить 1 треугольник. Тогда получается, что ответ всегда есть. Можно довольно просто доказать, что мы уложимся в 100. Асимптотика решения O(n3).
Доказательство
- Первыми несколькими шагами алгоритма мы сгенерируем полный граф. Потому что каждое ребро можно будет добавить
- Полученное количество треугольников — C(p, 3) для какого-то p. C(p, 3) ≤ k при этом p максимально.
- Для данных ограничений p ≤ 85.
- После первой фазы алгоритма, если из некоторой вершины мы добавляем u ребер, то количество треугольников увеличивается на C(u, 2).
- Получается, мы представляем маленькое число ≤ C(85, 2) в виде суммы C(i, 2).
- Первое число, которое мы вычтем, будет отличаться от нашего не более чем на C(85, 1) = 85, поскольку C(n, k) - C(n - 1, k) = C(n - 1, k - 1).
- Второе число — не более чем на C(14, 1) = 14.
- Далее можно применять данную оценку аналогично.
- Для всех возможных k данный алгоритм укладывается в 90 вершин.
Может быть есть что-то более красивое, но вообще на контесте можно было остановиться пункте на пятом и забить.
Идея: tunyash, Skird Реализация: tunyash Разбор: tunyash
- Пусть si — количество точек в столбце i.
- На картинке изображены два соседних квадрата n × n, A — количество вершин в левой части рисунка (это один столбец), B — количество точек в средней области и C — количество точек в правой области (это тоже один столбец). По условию, имеем:
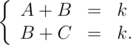
- Следовательно A = C.
- Таким образом
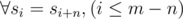
- Разделим столбцы на классы эквивалентности по признаку
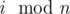 . Для всех a и b из одного класса sa = sb.
. Для всех a и b из одного класса sa = sb. - cnta — количество столбцов в классе с
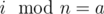 .
. - Существует (Cnk)cnta способов нарисовать по x точек в каждом из столбцов этого класса независимо от других классов.
- dp[i][j] — количество способов заполнить классы 1, ... i таким образом, что
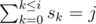 .
. 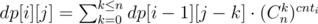
- cnti принимает
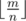 и
и 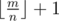 . Посчитаем (Cna)cnti для всех a и cnti и будем использовать при подсчете дп. Получаем сложность O(n2·k).
. Посчитаем (Cna)cnti для всех a и cnti и будем использовать при подсчете дп. Получаем сложность O(n2·k).
Идея: tunyash, Gerald Реализация: tunyash, Gerald Разбор: tunyash
Будем рекурсивно разворачивать граф, сводя задачу к поиску кратч. пути в графаз меньших порядков. Заметим, что вершина |D(n - 1)| + 1 — точка сочленения (кроме случаев n ≤ 2, но для них описанные ниже равенства так же выполняются).
Тогда, если вершины находятся по разные стороны от нее, то путь обязательно через нее проходит.
Пусть dist(a, b, n) — длина кратчайшего пути между a и b в графе порядка n.
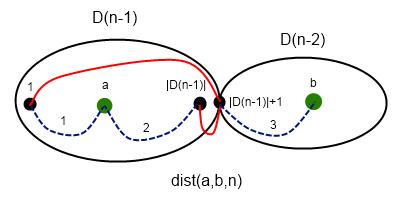
Красным обозначены ребра, синим — пути. Записанная формула обозначает, что мы можем пойти из вершины a по пути 1 в вершину 1, затем по прямому ребру в вершину |D(n - 1)| + 1 и по пути 3 в вершину b, либо пойти по пути 2, попасть в вершину |D(n - 1)|, пройти по ребру в вершину |D(n - 1)| + 1, а затем по пути 3 в вершину b. Если обе вершины лежат в меньшей половине графа — то
Если они лежат в большей половине, то нужно дополнительно разобрать случай прохождения пути через точку сочленения, то есть
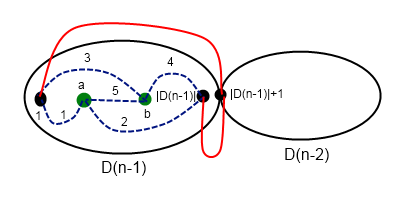
Если искомый путь проходит через точку сочленения, то для каждой вершины мы можем пройти либо в вершину 1, либо в вершину |D(n - 1)| + 1, а затем по прямому ребру в вершину |D(n - 1)| + 1. Если путь не проходит через точку сочленения, то рассмотрим его в графе меньшего порядка.
Можно заметить, что для каждого k будет не более 4 различных запусков dist(i, j, n).
Как это понять? Во первых, если отбросить запросы, где либо a = 1, либо b = |D(n)|, все запросы получаются из первого последовательным отнятием от изначальной пары (ai, bi) одинаковых чисел Фибоначчи (по построению D(i) — числа Фибоначчи). Получается, таких запросов будет O(n). Запросы вида (1, a) и (a, |D(n)|) можно рассмотреть отдельно, они хорошо выражаются из самих себя. Учитывая то, что все другие запросы получаются друг из друга прибавлением или отнятием чисел Фибоначчи, запросы этого вида тоже будут получаться друг из друга таким образом. Таким образом, у нас будет не более O(1) серий по O(n) запросов. Это не совсем строго, но, вроде, понятно. Это довольно нетривиальный момент, рекомендую задавать вопросы, если непонятно.
Получим асимптотику 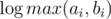 на запрос (логарифм возникает из соображения о том, что размеры графов в зависимости от порядка растут экспоненциально). Важно было запускать алгоритм не для данного n, а для наименьшего n, такого, что max(a, b) ≤ D(n - 1)
на запрос (логарифм возникает из соображения о том, что размеры графов в зависимости от порядка растут экспоненциально). Важно было запускать алгоритм не для данного n, а для наименьшего n, такого, что max(a, b) ≤ D(n - 1)
Идея: tunyash, Gerald Реализация: fdoer Разбор: fdoer
В разборе этой задачи подразумевается, что читатель имеет представление о суффиксных массивах и о быстром нахождении lcp (наибольшего общего префикса) двух суффиксов строки. Об этом можно почитать, например, на e-maxx.ru.
Итак, пусть d и d' — массивы такие, что di = hi - hi + 1, d'i = - di для любого 1 ≤ i ≤ (n - 1). Тогда мы можем переформулировать условие, при котором два куска забора считаются подходящими, следующим образом:
- куски не пересекаются, то есть, нет ни одной доски, такой, что она содержится в обоих кусках забора;
- куски имеют одинаковую ширину;
- для любого i (0 ≤ i ≤ r1 - l1 - 1) выполняется dl1 + i = d'l2 + i (если ширина забора — 1, это выполняется всегда).
Отсюда возникает следующая идея: для ответа на запрос нам достаточно узнать, сколько подотрезков массива d' длины (r - l) совпадают с отрезком массива d, соответствующим этому запросу, и при этом не пересекаются с ним ни в каком индексе. Построим суффиксный массив sa на последовательности-конкатенации массивов d и d', между которыми поставим еще разделитель — число, которого ни в одном из этих массивов нет. Запомним также для каждого суффикса di его позицию posi в суффиксном массиве. При поступлении нового запроса на отрезке l...r все куски забора, подходящие по второму и третьему условиям, будут началами суффиксов, лежащих в суффиксном массиве подряд на позициях boundleft...boundright, причем boundleft ≤ posl ≤ boundright и lcp(boundleft...boundright) ≥ (r - l). Поэтому границы этого отрезка можно найти с помощью бинарного поиска. В зависимости от реализации функции lcp для отрезка значения bound мы определим за 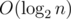 или за
или за 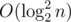 .
.
Теперь осталось найти число позиций из saboundleft...boundright, удовлетворяющих еще и первому условию, т.е. таких, которые соответствуют суффиксам d', префикс длины r - l которых не пересекается по индексам с отрезком (l...r - 1). Иными словами, количество i (boundleft ≤ i ≤ boundright) таких, что либо n + 1 ≤ sai ≤ n + l - (r - l) - 1, либо sai ≥ n + r (суффиксы d' начинаются в конкатенации с позиции n + 1, т.к. в массиве d (n - 1) элемент, а на n-ном месте расположен разделитель). Это тоже классическая задача поиска количества чисел из заданного диапазона на заданном отрезке массива, она может быть решена за 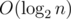 на запрос.
на запрос.
Её можно решать, например, offline с помощью метода scanline и любой структуры данных, поддерживающей запросы суммы на отрезке и увеличения в точке, либо online с помощью персистентных/двумерных структур вроде дерева отрезков.
Таким образом, вкратце алгоритм выглядит примерно так:
- построение массивов d и d'. Построение на конкатенации суффиксного массива.
- препроцессинг для вычисления lcp на отрезке
Для каждого запроса:
- определение промежутка (boundleft...boundright) с помощью двух бинарных поисков, обращающихся к lcp на отрезке.
- запрос на число суффиксов, которые лежат в суффиксном массиве на этом промежутке и которые соответствуют подотрезкам, не пересекающимся с отрезком запроса.
Если массив строить за 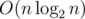 , запрос lcp выполнять за O(1) с предподсчетом за
, запрос lcp выполнять за O(1) с предподсчетом за 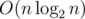 (с RMQ на разреженных таблицах), а числа из диапазона искать за
(с RMQ на разреженных таблицах), а числа из диапазона искать за 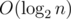 на запрос, итоговая асимптотика получается
на запрос, итоговая асимптотика получается 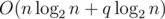 . Однако решения, выполняющие запрос lcp за логарифм с использованием, например, дерева отрезков, тоже укладывались в ограничения.
. Однако решения, выполняющие запрос lcp за логарифм с использованием, например, дерева отрезков, тоже укладывались в ограничения.
Идея: tunyash Реализация: tunyash, KAN Разбор: tunyash
Выберем центральный столбец на поле. Посчитаем для каждой клетки слева доступные на столбце, для каждой клетки справа те из которых доступна данная. Это простая динамика с битсетами, она полностью аналогична динамике в классической задачи о черепашке, 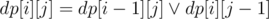 для правой половины доски.
для правой половины доски. 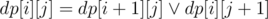 (
(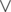 — логическое или, в данном случае имеется в виду побитовое или для масок) для левой. Динамика считаем маску доступных клеток на центральном столбце.
— логическое или, в данном случае имеется в виду побитовое или для масок) для левой. Динамика считаем маску доступных клеток на центральном столбце.

С помощью этих данных мы получим ответы на все запросы, точки которых лежат по разные стороны от выбранного столбца за n/32 на запрос (просто сделаем and битсетов). На картинке кружочками обведены две клетки, через которые может проходить путь между точками запроса.
Далее запустимся от двух половинок доски, выполняя тот же алгоритм. Получается время работы 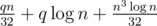 .
.
Запросы можно выполнять онлайн, храня для каждой клетки 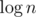 битсетов — множеств доступных клеток на столбцах, выбираемых центральными.
битсетов — множеств доступных клеток на столбцах, выбираемых центральными.
Альтернативное решение от mrNobody. Оно оказалось быстрее и проще авторского, но, к сожалению, он не смог сдать его на контесте.
- Будем считать динамику range[i][j][k] — самую верхнюю и самую нижнюю клетку столбца k, доступную из клетки (i, j). Ее можно считать аналогично динамике из авторского решения.
- Кроме того посчитаем динамику able[i][j][k] — доступна ли хотя бы одна клетка столбца k из клетки (i, j) при движении влево и вверх.
- Обе эти динамики можно посчитать за O(n·m2) времени и памяти (потом будет понятно, что на памяти можно сэкономить).
- Рассмотрим запрос (x1, y1) (x2, y2). Утверждается, что путь из (x1, y1) (x2, y2) существует тогда и только тогда, когда
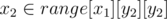 и верно able[x2][y2][y1].
и верно able[x2][y2][y1].
- Действительно, рассмотрим три пути. 1 — из (x1, y1) в самую верхнюю доступную клетку столбца y2. 2 — из (x1, y1) в самую нижнюю доступную клетку столбца y2 и 3 — из (x2, y2) в одну из клеток столбца y1. Если эта клетка расположена ниже (x1, y1), то путь 3 пересекает путь 2, а значит мы можем пройти по пути два до точки пересечения, а затем по пути 3 до точки (x2, y2).
- Случай пересечения путей 1 и 3 аналогичен.
- Мы получили решение за O(n·m2 + q) времени и такое же количество памяти, однако можно заметить, что хранить все состояния динамики не обязательно, достаточно только q из них. Пользуясь этим, можно сократить используемую память до O(nm + q).










В "Неквадратном уравнении" достаточно просто перебрать все числа от корня из N — 100 до корня из N.
я перебирал от корня из n и до тех пор пока позволяло время работы
У меня бинпоиск прошёл:) Функция не строго монотонная, но скачет не сильно.
а как ты с бинпоиском сделал.... в конце что нужно проверять перед тем как l,r- присваевать значения
Я туплю, до меня не доходит, почему это верно. Объясните, пожалуйста
s(x) << x при больших x => sqr(x) ~ n.
А где задача "Таблица"?
нету
появилось кратко.
как доказывается что в С найдётся ответ причём быстро? я добавлял рёбра оба фора 1..n у меня TL
так понятнее?
I believe there is an error in the DIV2 B problem. The range of s(x) should be 0 <= s(x) <= 81 because: sqrt( 10 ^18 ) = 10^9. So the biggest value s(x) will be when x = 10^9-1: s(x) = 9*9 = 81.
if s(x) <= 81 then s(x) <= 90, isn't it?
PRETTY MUCH YEAH BUT IT STILL DOES THE PART OF MAKING THE EXPLANATION CONFUSING.
Задача B интересна приколом разбиения на две динамики.
For Div 2 A, there is no answer when n is odd, not only when n = 1.
Yes, you are right. Thank you.
deleted: sorry misunderstanding
why is it -1 for all odd numbers?
i can make something like this when n=3
3 1 2 here P1=3 P2=1 P3=2
we know Pp1=1 so by comparing p1=2 Pp2=2 so p2=3 and p3=1
so every condition is getting satisfied. why is it -1 then?
$$$P_{P_{i}}=i$$$, so $$$P_{P_{1}}=1$$$ but in your case $$$P_{1}=3$$$ so $$$P_{P_{1}}=P_{3}=2\ne{1}$$$ , hence the condition is false. Every node in this array forms a cycle with another node, so it will never be possible to solve it for odd $$$n$$$.
Thank you epsilon_573
in doe graphs problem. 1 6 1 13 for this input answer 2 but i dont understand.can someone explain me.pleas write path from 1 to 13
1 -> 14 -> 13
|D(13)|=?
sory |D(6)|=?
|D(0)| = 1, |D(1)| = 2, |D(2)| = 3, |D(3)| = 5, |D(4)| = 8, |D(5)| = 13, |D(6)| = 21
Чекер как-то странно работает: в задании В на числе 10000006999999929 программа, запущенная в студии, дает правильный результат, а на сайте дает -1.
Код:
http://pastebin.ru/d9YHTI8q
Код убрал из предыдущего сообщения, так как форматтер работает плохо
Посмотри на панель инструментов и врапни исходник кнопкой Block
Код:
результат врапа
Ты просто не умеешь их готовить
Скорее всего проблема в использовании
doubleтам, где не надо. При работе с числами с плавающей точкой надо быть осторожным, поскольку вычисления не абсолютно точны. В частности, лучше не сравниватьdoubleс 0, а вместо этого делатьfabs(expr) <= eps,eps— константа порядка 10 - 6…10 - 9. Вообще, если есть возможность вести вычисления в целочисленных типах, то лучше ею воспользоваться.В этой задаче предлагаю сделать
, и далее
doubleне использовать вообще.P.S. Если локально код пишется под VS, то и на сервере лучше выбирать тот же компилятор, MS C++ — будет меньше сюрпризов.
Вопрос по 232C — Графы Доу Как я понял на каждой итерации по k, мы получаем всего 4 различных запроса и как-то должны их хранить, чтобы не опускаться в следующий раз глубже в рекурсию. Так вот сообственно вопрос: как это лучше делать, и сохраняем мы запросы вида d(i,j,n) где i и j отличны от 1 и |D(n)| ?
Делаем массив из четырех элементов для каждого k и пробегаемся по нему при вызове dist(i, j, k).
готов согласиться что у меня руки кривые((
I'm having trouble understanding this part:
Thank you.
Look, we have some full graph. We add one vertex with q edges starting form it. Is it clear, that we added Cq2 triangles to our graph? It it's not, you may check it with pen and paper. Number of vertexes in full part of our graph is p and Cp3 ≤ k. p is maximal possible value such that Cp3 ≤ k. Therefore k ≤ Cp + 13 and k - Cp3 ≤ (Cp + 13 - Cp3. k - Cp3 ≤ Cp2. Ok? We add new vertex with q edges. We will add Cq2 triangles to our graph and q is maximal. Therefore k - Cp3 - Cq2 ≤ Cq1 = q. We have x = Cp3 + Cq2 triangles in out graph and difference with k is no more than q ≤ p ≤ 85. If we will repeat adding vertex five or six time difference between k and number of triangles will become zero.
Got it. Thanks!
Please check the last case of problem c div 1. There are some mistakes with the formula.
Where?
You lost a bracket. Is it before or after "+ 2"? ^^
Thank you, I see.
Didn't understand editorial for "Quick Tortoise". Somebody please explain in detail.
Basically, the simple way to solve this problem would be to precompute if it's possible to get from (x1,y1) to (x2,y2) for all possible (x1,y1) and (x2,y2). This would take O(n^4) time and space so with n as large as 500 it won't work.
The idea for speeding this up is to use divide & conquer. The editorial splits the board by columns, and I did it by rows in my solution (and that is probably more cache-efficient, although that doesn't really matter) — either way will work fine.
Imagine first that every query you get was such that (x1,y1) is in the top half of the board and (x2,y2) is in the bottom half of the board. Then you could answer each query by the following procedure: 1. find all the cells in the middle row of the board reachable from (x1,y1) 2. find all the cells in the middle row of the board from which you can reach (x2,y2) 3. you answer "Yes" iff the results of 1. and 2. intersect
You can precompute the answers for 1 and 2 using dynamic programming. As O(n) cells of the middle row could be reachable from any cell, you could use O(n^3) time and space to compute the answers for 1 and 2. Using a bit set (the bitset class in C++ for example), you can reduce that to ~(n^3)/32 assuming you implement the bit set as an array of 32-bit ints. So for subproblem 1, for each cell, you store a bit set that indicates if you can reach a certain column of the middle row or not. You can compute each bit set via two bit set operations by the rules of the game.
Now back to the original problem. If the query is not of the form discussed above, then it is either entirely in the top half of the board, or it is entirely in the bottom half of the board. Therefore, you build an almost-complete binary tree structure. At every node of this tree, you solve the same problem discussed above for a certain row-slice of the board. The depth of this tree is about lg(#rows). You can precompute this tree before any queries are processed.
Then, for each query, you just walk down the tree to the appropriate row-slice of the board and look up the precomputed answers to subproblems 1 and 2 and return the answer. For implementation details of exactly this idea, you can look at my solution http://codeforces.net/contest/232/submission/2471344.
I didn't understand the analysis of the solution of "Table" problem. Can anyone help me and explain it in more details please?
I have a different weird solution for 233B: after looking for x for many different n values, I have noticed that the answer is always close to sqrt(n) so I just looked for a suitable x from sqrt(n)-100 to sqrt(n)+100
for even ones can we write 1 2 3 4 as 4 3 2 1 it also satisfies the condition pi!=i and ppi=i why not writing