Предлагаю поделится здесь своими мыслями по поводу задач.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:10:44
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:10:44
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 10:24:16 (j3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Мне интересно как участники решали К, I, D ?
Задачу I решали так: Запишем строку в виде a...ab...b Если количество букв будет равным и будет равно k, то получаемое значение на выходе k^2 Найдем первый квадрат не превосходящий n. Добавляя буквы (a) в конец строки (не более двух раз),сдвигая их влево и пересчитывая текущее значение — найдем удовлетворяющую нас строку.
а почему не более двух раз? или это такая магия?
Если более двух раз — то не получим минимальной длины.
Задача D:
Если n%2=1 ans=n*(n-1)*3+1;
Если n%2=0 ans=(n-1)*(n-1)*3+1;
код:
эх, мы циклом решали, мучались, а почему такой ответ?
Формула включений-исключений. 1 условие — n^2, 2 условия — n и 2n для нечетных и четных, 3 условия — 1 и 4.
признаюсь честно, ничего не понял, можете более подробно объяснить? что такое n и n^2?
Рассмотрим сколько возможных троек может быть.
1) Выполняется только одно условие: (ai + aj) % n = ak
2) Выполняются только два условия: (ai + aj) % n = ak и (ai + ak) % n = aj
1) Выполняются все три условия (ai + aj) % n = ak, (ai + ak) % n = aj и (aj + ak) % n = ai
Подсчитаем мощности множеств:
1) n^2 (два первых определяют третье)
2) При нечетных n (если ai = 0). При четных 2n (если ai = 0 или ai = n/2).
3) При нечетных 1 (ai = aj = ak = 0). При четных 4 (тоже самое + если 2 равны n/2).
not bad, спасибо
Как решалась B?
У кого-нибудь есть идеи/знание того, что за третий тест в задаче Н div 1? У нас решение находит 100% правильных ответов при стресстесте, однако при посылке мы получаем WA3 =(
Видимо, это тест, в котором нету ни одного удаления символа и цикл повторяется ровно 20 раз :(
сдал?
Сдал =/
у нас стояла проверка допустимости длины цикла:
if (n * 20 < s.size()) continue;(т.е. если у нас символов больше, чем текущая длина цикла, умноженная на максимальное количество повторений, то длина цикла n не может быть).При этом, к сожалению, при определённых условиях наш алгоритм мог добавить в начало строки лишний Х. Этот Х, на самом деле, ничем не вредит... кроме вот этого условия :((( т.е. нужно было проверить
n * 20 < s.size() + 3, например... эх.Если что самые выносящие тесты это буква I и буква П повернутые на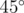 . Это вроде 46 и 49.
. Это вроде 46 и 49.
А что, правда никто кроме меня не заинтересовался, как кто решал H? Не нашел про нее вопросов, кроме этого.
Я примерно расскажу авторское решение.
Когда это решение стало достаточно надёжно находить ответ (стало работать без ошибок на 10 случайных инкарнациях каждого из 107 тестов), задача была объявлена готовой.
как решить задачи C и F?
Задача C.
С последними цифрами понятно: надо просто посчитать все по модулю 10.
С первыми цифрами зашло следующее: храним числа в long long, как только оно становится больше 10^18, делим его на 10^18. Первая цифра всегда корректная получается. Доказывать не умеем.
Мы сдали без магии с
long long.Считаем в double, как только число превышает 10, делим его на 10. Тогда первая цифра точно корректная получается.
И чем это решение отличается от решения с long long?
Почти ничем, если делить не на 1018, а на 10 (как на самом деле и написано в решении dalex). А иначе очень даже отличается =) .
Действительно, в этой задаче можно считать и в long long, и в double, и перейдя к логарифмам: погрешность во всех этих случаях не успевает доползти до значащих цифр.
упс... я оказывается невнимательно прочитал:)
Мантисса в
doubleпозволяет хранить не более 15 десятичных разрядов. Это даже меньше, чем сlong long.P.S. Как нормально решать C?
судя по высказываниям Gassa, авторы подразумевали именно такое решение
Вообще, есть общая идея, как решать задачи вида: найти с каких цифр начинается число ab.
Пусть первая цифра числа ab это k. Тогда, существует такое p, что k*10p<=ab<(k+1)*10p. Возьмем логарифм по основанию 10 от всех частей: log(k) + p <= b*log(a) < log(k + 1) + p. Перенося p в центральную часть, будем иметь: log(k) <= b*log(a) – p < log(k+1). Теперь легко проверять утверждения вида: "верно ли, что ab начинается с цифры k?". Просто проверяем это для k=1..9 и находим ответ.
В качестве тренировки, могу предложить сдать задачу http://acmp.ru/index.asp?main=task&id_task=585.
А почему бы не избавиться от перебора k?
Казалось бы, у нас есть b, a, нашли p.
Теперь ответ = round_down(exp(b*log(a) — p)).
Мы просто не хотим, чтобы за нас считали экспоненту — так будем лишь сравнивать числа.
А почему плохо в данном случае ее посчитать?
1 <= exp <= 9
Т.е. я не заработал погрешность. Разве нет?
Сережа, погрешность не заработал, но экспонента очень долго считается (по крайней мере, у jvm). До шести раз дольше, чем даже просто цикл до 10 без break'ов. Почти как Duracell. :)
Задача F.
Генерируем простые числа до 2*10^6. Затем проделаем некое подобие решета: для каждого из этих простых чисел p[i] пройдемся по отрезку [A,B] с шагом p[i] (это работает где-то за N*log(N), где N — длина отрезка), и отметим, какое из чисел на этом отрезке делится на p[i] (все делители сохраняем в векторы).
Теперь для каждого числа из отрезка [A,B] мы знаем все простые делители, меньшие 2*10^6. Если есть простой делитель, больший 2*10^6, то он только один и входит в разложение в первой степени. Будем делить, пока можно, каждое из чисел отрезка на его уже найденные делители. Если в конце получилась не единица, то это еще один простой делитель данного числа из отрезка.
Теперь мы знаем все простые делители всех чисел из [A,B], и можно посчитать по определению функцию Эйлера и вывести ответ.
P.S. Возможно, это решение не совсем такое, как предполагалось авторами, т.к. пришлось немного пооптимайзить.
Можно обойтись без векторов. Сохраним числа a..b в массив. Каждое число из массива будем делить на его простой делитель пока оно на него делится, учитывая этот делитель в соответствующей phi[x]. В конце останется 1 либо простой делитель > 2 * 10 ^ 6. Если остался делитель, учитываем его в phi[x].
Решили, что плохо считать втупую, считали в логарифмах. (Дробные части логарифмов должны лежать в соотвествующих промежутках), заходит если на каждой итерации писать
curlog = i * log(a), а неcurlog += log(a)А где можно задачи посмотреть?
Тут
У кого-то было WA18 по E?
PS: Можно как-то смотреть тесты?
Как решать задачу A?
при N > 5 ответ всегда ноль
Видимо утверждается, что всегда найдется два подмножества с равной суммой. Как это нормально доказать?
перебором, например ;)
а нормально?) Ну вроде бы понятно, что крайний случай степени двойки должен быть, а дальше не понятно
UPD. Под катом неверная идея.
разности могут пересекаться по элементам, из которых они получены.
Да, я ошибся. Хотелось бы услышать доказательство, почему при 6 получаем гарантированно 0.
Оценки максимального n, при котором бывает ненулевой ответ, можно доказывать по принципу Дирихле, рассматривая сами числа (n < 31), их попарные разности (n < 9), суммы всех подмножеств (n < 8). Если суммы или попарные разности пересекаются — удалим одинаковые куски.
Оценку n ≤ 5 я не умею доказывать проще, чем конструированием всех тестов, на которых ответ ненулевой. Но, поскольку фактически она верна, любой из предыдущих оценок хватает, если для остальных случаев написать перебор и вставить в него отсечения по нулю во всех местах.
не успел написать тоже самое что ниже, да и разностей при 6 будет не более 15, разве нет?
На самом деле не больше 21, нужно учитывать еще сами элементы.
Вроде не разборе говорили цифру 6. И умеют доказывать для 8. У нас тоже было 8, перебор заходит с отсечением "если есть два одинаковых то 0".
UPD. Я уже торможу. Это ≥ 6, так что все хорошо.
Для n>5 ответ всегда равен 0. А для пяти чисел пишем полный перебор.
Как решать K?
Я думаю для начала разбить на 3 случая: // обозначим первый отрезок за 'а' второй за 'b' 1 случай: Если отрезки a и b параллельны осям координат то 1. если они равны можно вывести 2 случайных числа желательно взять их по модулю больше 1000 2. если они не равны можно выводить "NO" т.к у двух треугольников будет одинаковая высота но разные основания => две одинаковые площади быть не могут.
2 случай: Если две прямые перпендикулярны тогда сравним площади треугольников 0,5 * |a| * h1 = 0.5 * |b| * h2 |a| * h1 == |b| * h2
вместо h1 напишем 1 получим h2 = |a|/|b| к координате X (от прямой параллельной оси ОУ) добавим h1 (т.е 1). А к У другой прямой добавим h2 получим координаты точки.
3 случай: две параллельные прямые не лежащие на 1ой прямой точка лежит между прямыми значит 0.5*a*h1 = 0.5*b*h2 h2 = x — h1; h1 = (a * x) / (a + b) а дальше аналогично
Дописать не успели в чём-то описался видимо пока писал исправить не успел WA 15 тест
Забыл дописать в конце проверку на NO, ва9. Добавил, градиентный спуск зашел.
правильно я понимаю, что на этих задачах проводился какой-то официальный тур? какой?
Это был XXXIII чемпионат СПбГУ. Если хочется отдельный монитор.
а почему было так мало задач? (ну обычно все таки 9 как минимум)
Ну.... скажем так.. Было слишком мало людей и времени. Хотя вопрос не совсем по адресу. Я все таки участник.
Так что призываю Gassa или Burunduk*
В целом, почему получилось всего 8 задач, не берусь сказать, я поздно присоединился к подготовке контеста. Лично у меня была возможность и желание сделать в субботу +1 задачу, но я предпочел потратить время на то, чтобы улучшить G (restore) и почекать остальные задачи.
В кубке сегодня были баги в условиях, тестах, с TL-ями? Про кубок я точно не знаю, не успевал следить. А у нас, на чемпионате СПБГУ вроде всё гладко :-)
ну то что это один из тех опенкапов, который всем более менее понравился, в котором почти не было ошибок (не считая чекера K) — это да, но все таки 8+ лучше 8) ну да ладно
Как решать G?
Перебор и пихать. Вот есть код. Правда от Dmitry_Egorov и после долгого пихания, так что мало что понятно.
а почему у вас долго не было апсептеда по G в мониторе?
ога, понятно
Получил ОК в дорешивании следующим перебором. Пусть первая точка будет иметь координаты (0,0). Выберем какое-нибудь рэндомное расстояние из имеющихся и скажем, что это будет расстояние между первой точкой и второй. Тогда сможем перебрать все возможные положения второй точки.
Теперь мы уже нашли координаты для двух точек. Найдем массив “кандидатов” на остальные точки. Как будем это делать? Просто переберем все расстояния d1 до первой точки и d2 до второй точки и проверим, что такая конфигурация возможна.
Теперь уже у нас есть координаты двух точек и массивы возможных положений остальных точек. Будем искать оставшиеся точки в порядке увеличения индекса в массиве кандидатов. При этом, в кандидатах будем поддерживать только тех, которых мы можем взять в нашем шаге рекурсии. То есть, если мы берем точку, то мы перебираем имеющихся кандидатов и выкидываем тех, которые уже не подходят. Имеется в виду, что если у нас есть уже координаты для первых x точек и мы проверяем какого-то кандидата, то мы должны убедиться что в списке допустимых расстояний есть все расстояния от кандидата до уже имеющихся точек. Эта часть у меня была реализована за C*x*log(D), где C – количество кандидатов, x – количество уже поставленных точек, D – количество различных расстояний во входных данных.
Локально такое решение работало довольно быстро, но на сервере сначала получало ТЛ. Тогда я сделал random_shuffle() входных расстояний и получил более дальний ТЛ :) Добавил srand(time(0)) и получился ОК :)
Небольшое упрощение — не надо отдельно генерить вторую точку. Можно уже от (0,0) найти всех возможных кандидатов и сразу же запустить перебор. Еще, вероятно, хорошо работает отсечение, что кандидатов должно быть не меньше чем непоставленных точек — для неправильных конфигураций мы часто отсекаемся на пару шагов раньше. Довольно аккуратную реализацию можно увидеть выше, по словам Burunduk1 оно работает 3 секунды, его решение — 1,3, но он выделял 200 метров памяти, вместо лишнего логарифма. Еще он добавил, что самые сложные тесты — рандомные точки в очень маленьком квадрате, когда много совпадающих длин (как мне кажется, это из-за того что плохо работает критерий "точка подходит, если существуют хотя бы один экземпляр расстояний до всех уже поставленных точек).
P.s. У нас TL был 5 секунд, возможно, на кубке был другой, т.к. сервера разные.
Почти как мое (авторское).
Рассказываю мое решение:
1) Основа перебора
2) Оптимизации
UPD: Как правильно выше говорит Дима, я хранил cnt[D], где D=0..2*108
random_shuffle и сортировка по убыванию |(dx, dy)| — одновременно?) Если серьезно, то зачем random_shuffle? Как он тут может повлиять на сложность решения? Пусть есть алгоритм A без random_shuffle и алгоритм B без random_shuffle. Тогда если A работает медленно на тесте T, а random_shuffle(T') = T, то B работает медленно на T'.
То есть все-таки в данном случае решение с random_shuffle — это способ пройти данные конкретные тесты, а не "любые возможные по условию задачи тесты"? А в авторском решении ведь должно быть все же последнее, или у меня устаревшие взгляды?
1) У меня есть 3 решения, одно делать random_shuffle, второе sort, третье половину времени ищет так, половину времени ищет так. Т.е. при желании можно и одновременно ;-) Более того, некоторым решениям такой фокус мог помочь уложиться в TL.
2) Про то, зачем нужен random_shuffle. Есть, например, такой объект, случайное двоичное дерево. Оно имеет глубину O(logN). А вот обычное двоичное дерево в худшем случае имеет глубину O(N). Так появляется Декартово Дерево (поддерживаем свойство случайности, это гаранитрует малую глубину). Вроде бы, ускорение на лицо... Почему есть сомнения, что такого не может произойти в других задачах?
Ну видимо если говорить формально, то ты путаешь понятия "асимптотика времени работы" и "асимптотика мат.ожидание времени работы.". Видимо первое формально не улучшается. Просто вероятность большого времени работы крайне мала.
Ну... возможно) Но слово "асимптотика" выше не присутствует. А вульгарные выражения типа "глубина декартова дерева — логарифм" настолько приелись, что никого не удивляют :-)
И еще, кажись, правильно говорить не "в худшем случае O(N)", а "в худшем случае Θ(N)". В этом плане я стараюсь, но иногда все еще забываю.
Оно присутствует у тебя ниже.
Ну Θ(N) это просто больше информации, чем O(n), а не более правильно. Ну обычно информация об оценке снизу не содержательная.
На тему "мощь random_shuffle" часто еще приводят такие примеры:
Покрытие точек кругом min радиуса за O(N)
Построение Триангуляции Делоне (и вместе с ней Диаграммы Вороного) через итеративное добавление точек в случайном порядке за O(NlogN).
Построение трехмерной выпуклой оболочки за O(NlogN), опять же путем добавления точек в порядке random_shuffle.
Во всех трех случаях применение random_shuffle к входным данным дает улучшение асимптотики.
P.S. В данной задаче, возможно, это было не асимптотическое, а "просто в 5-10 раз" ускорение, но эффект таки закономерен :-)
Отличие только в том, что про покрытие точек кругом я умею доказывать, что за счет этого мат. ожидание времени работы O(N). А еще QuickSort делает randomize. А ты пытался доказать, что у тебя среднее время работы хорошее? Или там все слишком сложно?
Доказать я не смог.
Stress по 10 000 тестов с маленькими координатами , маленькими + гомотетия, большими координатами отклонений по времени для random_shuffle не нашел. Для решения без random_shuffle и sort отклонения регулярно встречаются.
Расскажите, как решить E?
Все точки можно разместить на решетке 6*6. Перебираем все комбинации точек и проверяем, что условия выполняются. Если нужно, можно добавить отсечений в перебор.
Мы захардкодили все возможные расположения точек (для n <= 6 таких расположений 22 штуки), а потом проверяли все расположения для данного n, для каждого расположения проверяли все перестановки точек, а потом смотрели, подходит ли инпут под данное расположение.
Мы решали так. Есть есть прямая на которой ровно одна точка — выкинули (как нибудь проведем). Если есть прямая, которая проходит через две точки, то тоже выкинули. Но в конце проверили что на нее случайно ничего не попало. Если попало, то сказали, что неудача и сгенили заново.
Если есть точка, лежащая только на одной прямой, то выкинули, потом добавим в случайное место. Итого на всех прямых лежит по хотя бы три точки, и каждая точка лежит на хотя бы двух прямых. Несложно понять, что единственная картинка которая бывает (ну или ее подкартинки) — это четыре прямые, на которых лежат по три точки, каждая точка лежит на двух прямых. Такая делается руками.
Мы генерили набор случайных точек с координатами от 1 до 8 и проверяли, подходит ли он под инпут. Если не подходит, то генерим заново. Если за 1.9 секунд не нашли ответа, то выводим "NO". Такое решение не находит ответа для 6 точек на 1 прямой, так что это отдельно рассмотрели. Еще у нас на один тест ответ находило в зависимсти от randseed, так что мы на всякий случай его тоже руками вбили.
А когда возможен NO, кроме следующего случая? если есть два неравных множества с пересечением больше одного элемента.
Виталик говорил на разборе, что такие случаи появились бы для девяти и десяти точек.