khadaev's blog

Codeforces Round #443. Editorial
By khadaev, 7 years ago, translation, In English
Div 2 A
Div 2 B
Div 2 C = Div 1 A
Div 2 D = Div 1 B
Div 2 E = Div 1 C
Div 1 D
Div 1 E
  • Vote: I like it
  • +137
  • Vote: I do not like it

Comments Comments (33)
| Write comment?
»
7 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Auto comment: topic has been translated by khadaev (original revision, translated revision, compare)

→ Reply
»
7 years ago, # |
  Vote: I like it +18 Vote: I do not like it

I have learned SCC(strongly connected components) recently. But I can't figure out the solution of div1 C/ div2 E. After I understand the solution of choice (id: 31775120), I think it is so simple and beautiful!

Then I consider why I can't get the solution? Maybe it requires kind of mathematical intuition.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I think the solution of DIV2 D can be easier when i saw this solution 31763303

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

Div 2 C / Div 1 A Bonus solution :
Approach 1. Don't use AND operation at all. All four cases can be handled with just OR and XOR operations. For example , if (0,1) and (1,0) are the (input,output) pairs you can do OR 0 , XOR 1.

Approach 2. Say X is the output you get when the input is 0 and Y is the output you get when the input is 1023. We can just do these two operations : AND (X ^ Y) , XOR X.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you please explain why the second approach works? Thank you.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      1023 = ten1's, 0 = ten0's. so when we apply all operations to these two numbers we can determine what operation(flip, nochange, set0, set1) is happening to a certain bit.

      Now we can choose either ^and| as our two operations or ^and&. My solution uses ^and|.

      Concretely, let op0 be output of all operations applied on 0, and op1 be the output when applied to 1023.Consider what should the ith bit of number_to_be_xor'red_with and number_to_be_or'ed_with be, for a given ith bit of op0 and op1.

      • op0:_______0 0 1 1
      • op1:_______0 1 0 1
      • __________________
      • xornum:____1 0 1 0
      • ornum:_____1 0 0 1

      now observe that xornum is 1 when op0 is 0, so xornum=~op0 and ornum is 1 for ~(op0^op1). Now since these are bitwise operators, applying on the bits 1 by 1 is the same as applying on whole number.

      Therefore, xornum=~op0, ornum=~(op0^op1)

      Implementation Detail: We need to consider first 10 bits only(0<=xornum,,ornum<=1023), so & xornum and ornum with 1023(bits greater than the 10th one will be set to 0).

      The solution given here has the simplification with ^and| instead of ^and&, but the concept is same.

      Accepted Solution: http://codeforces.net/contest/879/submission/31857500

      Thank you original author for the idea!

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Can you please explain this for a single bit? I still do not understand how this compacts and, xor, and or.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          lets assume we have only 1 bit numbers. so op0 op1 xornum and ornum are all 1 bit. Applying all operations on 1 and 0, we can have 4 possible cases ->

          op0 is 0 and op1 is 0, in this case, we have set 1 to a 0, and 0 remains as it is, hence we can say that no matter the value of the bit we have made it 0, to do that, first or with 1(set1) and xor with 1(flip).

          op0 is 0 and op1 is 1, hence we have just passed the number as it is (i.e. 1->1 and 0->0). Hence do nothing, i.e. xor with 0 and or with 0.

          op0 is 1 and op 1 is 1, this is set 1 operation(like case 1 but now we set it to 1). To do that or with 1 and xor with 0.

          op0 is 1 and op1 is 0, clearly we have just flipped the input bit, i.e. or with 0 and xor with 1.

          Ultimately you just have to figure what should each bit turn to after the operations and how to achieve that using xor and or (and adjust that bit accordingly)

          → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Maybe the time of Soluton of Div1 C is wrong?I think if we use balance binary search tree(what's "a some search tree",I can't understand),the time will be O(klogn) once?Because once comparing is O(k),not O(1).

→ Reply
»
7 years ago, # |
  Vote: I like it +48 Vote: I do not like it

I suppose I have an O(n) ONLINE solution for 878E - Numbers on the blackboard. Please correct me if I have made a mistake. Here it is:

We call the action mentioned in the problem statement "merge x, y".

Define f(i, j) (i <  = j) as: Consider subarray a[i...j] and each time merge two last elements until one number is left. f(i, j) is that number. Let L[j] be the maximum i(i <  = j) that f(i, j) <  = 0. If there is no such i then L[j] = 1. Now for each index j define par[j] = L[j] - 1. Build a tree using array par[].

Now we are going to answer query li, ri in O(1). First find the lowest ancestor of ri in the tree which is inside the query and name it g. You can prove:

answer = A + 2 * B.
B = 2 * (f(L[ri], ri) + f(L[par[ri]], par[ri]) + ... + f(g + 1, ...))
A = f(li, g)

For better understanding take a look at the picture below.

If we can find g in efficient time, the rest is not very hard: We calculate B using a partial-sum on tree and calculate A using another simple partial sum on suffixes of the array.
First sort children of each vertex in increasing order of difference between their index and their father index. Let D = lca(li, ri). g is a direct descendant of D. Now for calculating lca in O(1) we use the approach explained in this post (Advanced RMQ). BE CAREFUL to modify RMQ in a way that gives us the rightmost index with minimum value.
Let ind = index of rightmost D obtained by RMQ. You can prove g is located at ind + 1.

This approach solves the problem using O(n) preprocess (for building the tree and reduction of LCA to RMQ) and O(1) for each query.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Nice implementation for Div1A / Div2C: 31777939.

Edit: I didn't notice an even simpler solution here.

→ Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

Div 1 D:

Is this solution supposed to get AC?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I don't think so. It's clearly O(q^2).

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

For Div2 E/ Div1 C, does the statement condensation is a path mean that it'll be a chain and not a general DAG ? If we have 3 components C1,C2,C3 , why can't we have a DAG like C1 -> C2 , C2->C3 , C1->C3 ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Indeed, we can have that situation. The important thing to see, is that the partially ordered set induced by the condensation is in fact a total order. We can call that a chain (or path, as he did).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yes, i convince myself of that too, but mostly because i couldn't build any counterexample, so can you prove this interesting fact. I think the most important property of the graph is that every game forms a total order.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Well, yes. It is mentioned in the editorial as well. For any two components A and B, take any vertexes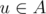 and 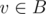. Since it is always true that u can beat v, or v can beat u, there are no incomparable components.

        → Reply
»
7 years ago, # |
  Vote: I like it +12 Vote: I do not like it

In Div1 D, can anyone explain why there are at most 2k different characteristics? I can't understand it since there are two kinds of spells......

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    If two characteristics are equal for all initial creatures, they are equal for all creatures. So, the characteristic is completely determined by the sequence of k zeroes or ones.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      Sorry, but I still not understand this. Lets say: n = 4, k = 3. The characteristics of these 3 creatures are:

      0: [0, 1, 0, 1]
1: [1, 0, 0, 1]
2: [1, 1, 1, 0]

      Now we can create the following other mixtures:

      3: [0, 0, 0, 1] (min of 0 and 1)
4: [1, 1, 0, 1] (max of 0 and 1)
5: [0, 1, 0, 0] (min of 0 and 2)
6: [1, 1, 1, 1] (max of 0 and 2)
7: [1, 0, 0, 0] (min of 1 and 2)
8: [0, 0, 0, 0] (min of 2 and 3)
9: [1, 1, 0, 0] (min of 4 and 2)

      This are already more than 2^k = 8.

      Do I completely misunderstand the problem?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +24 Vote: I do not like it

        he means to say that there are at most 2K distinct columns , any repeated column can be discarded and all instances of it from the queries can be replaced with the first occurrence of that column.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it -8 Vote: I do not like it

        As I understood, it makes at most 2k + 1 different sequences. Because same columns can get 0 or 1, that is why you got more then 8

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Why at most 2 ^ (k + 1) I still can't understand!

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Div2 D / Div1 B can you please explain the criteria of two participants being in the same the team?

→ Reply
»
7 years ago, # |
  Vote: I like it -8 Vote: I do not like it

I can't understand your greedy approach in div1E. Indeed, if you the last value is negative, you'd like its coefficient to be as small as possible (thus, equal to k[n-1]). If it's non-negative, yes we could double its coefficient (k[n] = k[n — 1] + 1), even though I'm not sure what it's supposed to be done if it is 0. The problem is the follow-up: now let's say we add some other number, a[n + 1] > 0. And we had a[n] < 0 and, therefore, decided to have k[n] = k[n — 1]. And now we obviously would choose to have k[n + 1] = k[n] + 1. The problem is: if 2 * a[n + 1] + a[n] > 0, then we might prefer to have k[n] = k[n — 1] + 1 as well. Could you try to better explain your solution? (maybe with an example) I'm not sure what you mean through block, but honestly, I just care about the greedy behind it, right now (to get an O(N) time complexity per query) and I'm not sure whether the blocks are meant to help me improve a solution that I supposedly already have or are meant to explain that solution (in linear time per query)

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    I have a solution that I think it's like editorial solution.

    define sum[l, r) = al * 20 + al + 1 * 21 + .... + ar - 1 * 2r - l - 1

    lets define f(i) as the maximal l such that sum[l, i) < 0 and if such l doesn't exist put f(i) = 0.

    you can see that if you want to answer the query [l, r) you should return the value of

    sum[f[r], r) + sum[f[f[r]], f[r]) + .... + sum[l, x) which x is the index where f(x) is less than l .

    now for solving question , when you add ith number you should f(i) .

    if it's negative , the f(i) = i - 1 _ so it's a new Block!

    otherwise these indexes are candidate to being as f(i) : f(i - 1), f(f(i - 1)), f(f(f(i - 1))), ... _ so this element makes a new block by merging some of the previous blocks!

    you can iterate over them and find the value of f(i) .

    after that you have the value of f(i) and you know the blocks and you can answer the queries!

    so I think word Block in editorial means the segment [f(i), i) !

    for checking details! 31832716

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    At first, if the last value is negative, k[n] = 1, not k[n-1].

    Of course, some k[i] can change when we add a number to the end. But I don't really understand where is the problem for the linear solution. In this case you can just re-find all k[i].

    Blocks are needed to implicitly store k[i]. Navick has already explained about them.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      Yes, you ‘re right but I Think editorial is not very useful,

      Because it does’nt say the meaning of Block!

      → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Div1B really has a good set of test cases, which tortured me long enough. Mean nothing bad.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have a question in the editorial for 1C, Tournament, about the part

"We need to find the weakest of those components that he can lose, and the strongest of those components that he can defeat. If the first component is stronger than the second, the new sportsman forms a new component. Otherwise, all the components between the first and the second merge into one, and the new sportsman joins it."

Why do we merge the components between the first and second? I have some intuition that it is because they are "equal", so they can beat each other with bidirectional edge, but I still am not sure exactly how this works. If anyone could explain, it would be much appreciated. Thank you.

→ Reply
»
4 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Editorial is broken. Doesn't show anything

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

C is harder version of 1608C?

→ Reply