Rim.K's blog

101 Hack 52 — Hackerrank
By Rim.K, history, 7 years ago, In English

Hello Codeforces community,

I would like to invite you to join HackerRank's 101 Hack 52 which starts at 1500 UTC, December 3, 2017.

There will be five tasks and three hours for you to solve them. The contest will be rated and the top ten contestants will receive HackerRank T-shirts!

The problems will have subtasks to make it interesting for everyone. I strongly recommend reading all the problems.

I’m the author of this round. Thanks to adamant for testing the problems, and thanks to kevinsogo for all the help in the other aspects of the contest. Also, thanks to Kerim.K and Infused for help in preparing the problems.

I hope you'll enjoy the problems!

Happy Coding!

Note: We are trying out a slightly different format on the challenges, let us know if you have any feedback.

  • Vote: I like it
  • +101
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +25 Vote: I do not like it

The f--- is strong with this one. Gotta participate.

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Just to remind: Contest starts in 25 minutes.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +51 Vote: I do not like it

Feedback on problems 1, 2, and 4: these tasks have something that isn't really a valid input provided as sample input in problem statement — things like "k=3" instead of a single number 3; moreover, even that invalid input can't be copied — it is provided in form of an image.

Please don't do it this way in future :)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    I didn't notice that. I always hit run code before submit and in case of errors you can copy example test easily from that window.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Can anyone explain O(n * (logn + log(Amax))) solution for the 4th problem???

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +27 Vote: I do not like it

    Clearly, there are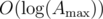 indices j, such that the value OR — AND for [i,j-1] and [i,j] is different. Lets call such j events.

    Now sort events in decreasing order, and divide [i,n] into contiguous parts for which only max and min change. If we traverse in decreasing order, we have to apply binary search on only one part to find the answer, as we apply binary search only when we are sure there is a solution in the part, which can be checked in O(1) using the left endpoint. Once we find such a part, we do binary search and get maximum possible j for this i

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +6 Vote: I do not like it

How to solve Car Show?I am not able to figure out how to use the good pairs, to answer all query?How to handle duplicates?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    For each index i, find rightmost possible j (let us store all such j in rightmost[]) such that the segment [i, j] has no duplicates. Build a persistent segment tree on rightmost[]. Given a query L-R, you need to find out the number of indices i such that L <= i <= R and rightmost[i] <= R and add rightmost[i]-i+1 for each of them. For all other i, assume rightmost[i] = R and add R-i+1 for each of them. You can use PST for this.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Same thing but sort the queries(by r) and use fenwick trees. It is easier to code compared to PST.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        What do you store in the tree? Sum of rightmost[i] or rightmost[i]-i+1? What is the time to answer a query — isn't it O(lg^2n)?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +6 Vote: I do not like it

          first find for each one rightmost[i] ,then sort them based on rightmost[i] .Also sort queries based on r value. Now for each query we need to know count of those whose rightmost[i] is more than r and sum of rightmost of those whose rightmost is less than equal to r. So we maintain two fenwick trees(one for storing whether rightmost[i]>r or not and other for storing sum of rightmost which are less than equal to r) and update them such that by the time we query for l to r .All those with righmost[i] less than equal to r are updated in them.So then after getting these two values later part is just basic math

          This takes O(logn) per query and overall complexity of O(n*logn)

          → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +2 Vote: I do not like it

        I used Binary Search for this problem. I guess it is easier to code compared to fenwick tree.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +8 Vote: I do not like it

          You are the best, forget the rest!

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it +2 Vote: I do not like it

            I guess this problem can be solved in O(n) if my solution is correct.

            → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 7   Vote: I like it +3 Vote: I do not like it

      thank you, got it :)

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Count rightmost possible indexes as already mentioned. Observe that they are non decreasing.

    Calculate prefix sums. pref[1] = rightmost[1], pref[i] = pref[i-1] + rightmost[i]-i+1 (the number of possible endings for intervals, which start at index <= i).

    For each query find the last index i, such that L <= i <= R and rightmost[i] <= R with binsearch. Now you can add pref[i]-pref[L-1] to the result (take each interval starting between L and i and add all possible endings, which fit within interval <= R). For the beginnings i+1,..,R you can assume that they end in R and you can calculate the number of intervals by simple formula (R-i)*(R-i+1)/2.

    → Reply