Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



Да можно и по обычному профилю. Выходит O(n·216·10) или O(n·212·10)
Hi! Just a small note about problem D.
In the editorial you said to subtract cntai * ai, but then you are adding cntai * ai again in the last sum, so you could just omit those two terms.
I know it adds the same, but I think is more natural for the understanding to just don't include them.
what is cnt?
cntx is the count of ocurrences of value x (at the left of i).
When you process the i - th number, you then add 1 to cntai
Isn't the time complexity for E gonna be O(n * n * n * k) ?
n *n -> generating all the possible string 't'.
n *k -> checking it will all the strings s1, s2 ... sn
If this complexity is right, then won't the above solution give TLE ?
It would have been really nice, if the author would have attached a sample submission.
Why it will be O(n3·k)? Authors solution generates O(n) strings t, for each string checking will be O(n·k) -> Complexity is O(n2·k). And my solution
Your solution is not accessible.Please correct it.
Fixed, sorry :)
There's a simple observation that can make the E solution a lot faster and less likely to get TLE. When you are determining the indices where si ≠ ti, if there are more than 4 such indices, then the answer is -1 (since s and t are too far from each other for there to exist a "base string"). Now you'll only have O(1) candidates for the "base string", and the rest of the approach is quite fast.
Oh my god, i use it in my solution but forgot to write it in editorial. Sorry!
Another solution for F:
Use DP state (i, mask) to mean the minimum cost to make everything before column i dots, and the columns i through i + 3 having asterisks in the positions indicated by mask (which ranges from 0 to 216 - 1). The transitions are to clear a square in the mask (1x1, 2x2, 3x3, or 4x4), or, if the bottom 4 bits of the mask are empty, to shift to column i + 1.
There are 1 + 4 + 9 + 16 = 30 transitions of the first type, and 0 or 1 transitions of the second type, so the total time is O(n·216·31). Implemented in a top-down (recursive) fashion, this doesn't run in time (submission: 33204536). The worst case is with a 4x1000 matrix, all asterisks, which takes about 5 minutes on my machine.
To speed it up, we note that if the bottom 4 bits are empty, the shifting transition is always best: we don't need to check all the square-clearing options. Furthermore, unless we are at i = n - 4, it is always best to clear squares that border the left edge of the square under consideration. This reduces the possible transitions by about a factor of 2, but it also drastically reduces the number of states visited: in the maximum case described above, our recursion only visits 106371 states, and the submission (33204643) passes in 61ms.
You need only 3 columns for DP.
Why are there only those 30 transitions? What if the last 4x4 square looks like this:
Which transition would be used to use 4 1x1 stamps to clear the leftmost asterisks?
Nevermind, I misread your solution.
Can someone explain the logic behind the solution of problem D please?
D can also be solved using a Fenwick tree. Go through the sequence of numbers from least to greatest, updating the tree from 0 to 1 as you go. For each new value, update all previous values more than 1 less than it in the Fenwick tree, then add val*query(0, ind-1) — val*query(ind+1, MAX_N-1) to the final answer. Then do the same thing again, but in reverse sorted order.
I cannot understand your solution my bad,can you explain using an example...
I will do the sample case:
The initial BIT is like this:
0 0 0 0 0We go through the elements in sorted order. So we start at 1, which are at indices 0 and 3. Before we look at 1, we have to update the BIT with all elements that are less than 1-1 = 0. There are none of these, so the BIT is still at
0 0 0 0 0. For the 1 at position 0, we add 1*(0) — 1*(0) to the final answer. For the one at 3, we also add 0 to the final answer.Now we go to 2. The only 2 is at index 1. Before adding the 2, we update the BIT with all elements less than 1, but there are none of these, so we don't update it. As before, add 0 to final answer.
Now we go to 3. They are at 2 and 4. First, update all elements less than 3-1=2. There are 2 of these: the 1 at index 0 and the 1 at index 3. So now our BIT looks like this:
1 0 0 1 0The 3's are here:For the first 3, we query for the sum of the first 2 elements of the BIT, which is 1. Then we query sum of last 2 elements, which is 1. So we add 3*(1) — 3*(1) to the final answer.
For the second 3, we query for the sum of the first 4 elements, which is 2. Then we query sum of last 0 elements, which is 0. So we add 3*(2) — 3*(0) to the final answer. Currently, the final answer is 6.
Now we go through and do the same thing in reverse sorted order. First, reset the BIT to all 0s.
For the 3s, we update all positions of elements greater than 3+1=4. There are none of these, so again add 0 to final answer.
For the 2s, update all positions of elements greater than 2+1=3. None, so add 0.
Now, the 1s. Update all positions of elements greater than 1+1=2. So our BIT becomes
0 0 1 0 1. The 1s are here:For the first 1, add 1*(0) — 1*(2) to final answer. For the second 1, add 1*(1) — 1*(1) to final answer.
Final answer: 4
I too taught of Fenwick tree but as array values are in order of 10^9. how to handle that much memory. Or i m doing something wrong here ?
The Fenwick tree only has order of 10^5 elements. You just have to process the elements in the correct order, so their max size doesn't really matter.
The answer for problem C is just the mode (the highest frequency among all numbers) of the array.
[deleted]
Can someone explain author's approach to the problem F in more detail? What is the bit mask representing, and how is he using it to form dp states?
very nice solution for problem G, thinking the min-cut way is much easier :-)
In problem D test 29's correct answer is -9999999990000000000. Isn't it exceeding 10^18 by it's absolute value?
Read the clarification carefully.
903F - Clear The Matrix What does mask mean? I am visualizing it like this.
~~~~~ mask = 1
for i = 3 and j = 4
|*|.|.|
|.|.|.|
|.|.|.|
|.|.|.|
mask = 3
for i = 3 and j = 4
|*|*|.|
|.|.|.|
|.|.|.|
|.|.|.|
~~~~~
Is this correct.
Its better to visualize it like
for j = 4
for j = 1
Then doing mask = mask >> 1 shifts it one cell further
I still don't get it. :-(
Can you give recurrence relations between state domains in 903F - Clear The Matrix.
Thanks in advance.
I can share my solution. I believe that it's pretty easy to understand with editorial given.
can you please understand the transitions i didn't get it from editorial. please help !
In problem D how to calculate that the absolute value of the answer will be up to 10^19?
please correct me if i'm wrong
let's make y-x value maximum so y must equal to 10^9 and x equal to 1
let's approximate maximum value of y-x to be 10^9
now let's make y-x occurs alot
consider this case : (n=4)
1 , 10^9 , 10^9 , 10^9
so y-x happens 3 times
now let's make n=2*10^5
so let's divide the array into two equal parts ones and (10^9) part
the array will be like this 1 1 1 1 1..... 10^9 10^9 10^9..
so for every one y-x happens 10^5 times
and we have 10^5 ones
so our value will be (10^5)*(10^5)*(10^9) = 10^19
sorry for poor english
Can someone explain problem D please?
In my opinion,
there are three major difficulties which could be encountered in Problem D:
The below is my attempt to explain the first two of the difficulties.
I do not know how to resolve the third one fast and bugless in C++ (I implemented a solution in practice mode but it takes too much time to be practical, i.e. to write it in a contest from scratch).
Thus,
I suggest to start with a simpler unconditional difference function: d'(x, y) = y - x.
I found it useful to imagine the problem with summation of d'(ai, aj) as a summation of elements of matrix D'
where D'i, j = d'(ai, aj), which means: D'i, j = aj - ai.
(It is convenient to write down ai values as both a header column and a header row of a table representing the D' matrix, thus filling the matrix with aj - ai values becomes a simple process if you want to do it on paper.)
An important condition is i ≤ j, which means that we consider the bottom-left triangle of D' to be filled with zeros.
We only need to work with the upper-right triangle of the matrix.
Note also that we can exclude the diagonal elements of D' from consideration (ak - ak ≡ 0).
Summation over D' is now straightforward but requires O(n2) iterations which is too much for n = 2·105.
So the point is how to optimize it.
Observe that for any k, the ak value is added to (or subtracted from) the final result many times.
If we could calculate the number of times in O(1) then we can replace multiple additions with a multiplication which means that we would need O(n) operations (addition, subtraction, multiplication) in total.
Calculating the number of times in O(1) is easy if we observe the following:
Now, the number of times is easy to calculate for any ak, so the summation over D' could be done in O(n).
This is the point where we return to the original d(x, y)
(and, thus, to the corresponding matrix D instead of simpler D')...
D could differ from D' only in those elements where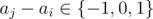 .
.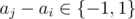 because Di, j = D'i, j = 0 if aj - ai = 0 (no need to fix).
because Di, j = D'i, j = 0 if aj - ai = 0 (no need to fix).
Actually, we can only consider
So, we are interested how to fix D' so that it would become equal to D...
For any ai, we could try to count how many aj can be found (j > i)
so that aj = ai - 1 (let's call it cnti, prev).
Likewise, how many aj can be found (cnti, next) so that aj = ai + 1.
Note that:
which means that we need to subtract 1·cnti, next from the D'-based result
and to subtract ( - 1)·cnti, prev from it.
This could be implemented in multiple ways.
All of them (which I could think of) require a map which would answer how many times a value is encountered in a[] sequence (i.e. how many distinct i exist so that ai = value).
In my demo implementation (33250280), I modify this map while iterating by i towards n
so that on each step cnti, prev and cnti, next can be easily taken.
Thank you very much for helping me understand the problem.
O(n·4·212).
Мои глаза...
4*2**12 — это константа.
Да, разумеется, это я и сам понимаю. Ну давай тогда говорить, что решение за O(n), чтобы всем все было понятно.
Бывают "переменные", которые не меняются от теста к тесту, а фиксируются в условии, и такие "переменные" в нашем случае можно без проблем задавать константами в записи асимптотики, дабы не усложнять ее.
Так-то авторы могли написать в разборе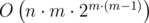 . Но зачем, если m = 4?
. Но зачем, если m = 4?
Это первый способ. Второй — сложность O(N), скрытая константа — 2**14. И оба хорошие.
Зачем использовать математические обозначения не по делу?
Мне кажется, что если "назвался груздем" (решил использовать обозначения), то "полезай в кузов" (используй их правильно)))
Can someone explain the solution to F?
For problem, A is this logic is correct or not
if(x%7==0 || x%3==0) _ print("YES");_ else if((x%7)%3 == 0) _ print("YES")_ else _ print("NO")_
It's not correct, because when you did (x%7) you divided x by 7, so you lost values that may be divisible by 3. For example, and as your logic says: x=19 -> (x%7)%3=2!=0 -> the answer is NO (here you made two meals by 7 and there was 5 remained), but we can make one meal by 7, and four meals by 3, so we obtain 1*7 + 4*3 = 19, and the answer for this sample is YES.
means the else if block has the wrong logic
Yes.
By the way, for any x > 11 the right answer is YES.
Wow, it's very good that by at least four 3's, it's guaranteed that we can make one 7 by adding one, and two 7's by adding two, and by adding 3 we come up with a number that's divisible by 3, and so on :D, Thanks.
You are welcome :)
I'm not sure I understood your logic, unfortunately.
I proved that property after trying to greedily construct all possible YES-numbers, in ascending order. I ended up with the following:
This means that, starting with three consequtive YES-numbers, all larger numbers are also YES-numbers.
The smallest three consequtive YES-numbers are:
P.S. I had not noticed this property myself. I found a solution which is based on this idea and wanted to check if I can hack it :)
Firstly, I'm sorry for these untidy comments... ( UPD : now this is tidy :) ).
Another "Wow!" for this prove which I was looking forward one like it.
My logic was that the number
12is the first number that contains at least four 3's3 + 3 + 3 + 3.Then the next number will contain
3 + 3 + 3 + 3 + 1and this additional1can be merged with two 3's obtaining3 + 3 + 7which gives us the answer YES..And the next number will make another single
1which also can be merged with the remained two 3's obtaining7+7-> YES..The next number is divisible by 3 -> YES, and so on.
It's guaranteed that this is true for all the next numbers because in all these numbers we have that four 3's which we need in merging, and after merging we will have some 7's and some 3's (may be 0).
P.S. I had not have this prove before I read your comment, Thanks.
Now I understood. Thanks for explaining!
In problem E, rather than swapping si,diffpos with any other character of si , Can't I swap it with any other character at a position in array pos?
Can anyone explain why we need previous 12 cells in problem F? Why not any other number?? Thanks in advance.
Can somebody help me in question E. My solution getting TLE , i have use hash like abc---> a*p^2 + b*p+ c , and try to find the intersection of all swap of all string
my solution link
I have another approach to problem E, which differs from that described in the editorial. I haven't proved it's correctness, and I'm not even sure if it's correct, but it passes the given 70 tests and I stress-tested it against a few other tests. It would be interesting to see if someone could hack it.
It stems from the brute force solution: just recursively iterate over all possible strings and check if each string is valid. The issue with the recursive solution (the reason why it's slow) is that sometimes, we know that a prefix is invalid. It's invalid if it's not a prefix of a permutation of the original input (i.e. it contains more occurrences of a given character than it should). It's also invalid if it differs by more than 2 from other strings in the input. Just using these 2 ideas to prune generates a pretty good brute force when $$$k$$$ is large, since it's highly unlikely that a given string satisfies those two criteria.
So now the issue is dealing with small $$$k$$$ ($$$k \le 10$$$). We can store what the interesting points are (points at which a swap may have occured) and try randomly swapping interesting points.
It turns out, to my surprise, that this actually works.
TL;DR Please hack me :).
143162377
certainly Education Forces have weird taste of fun