144A - Arrival of the General

We should find the maximum value with the minimum index and the minimum value with the maximum index, whose indices are denoted as id1 and id2 (index starts from 0), respectively.

If id1 = id2, it means that all the values are the same and thus no swap is necessary. If id1 < id2, it takes id1 steps to move the maximum value to the first position while n - 1 - id2 steps to move the minimum value to the last position, which gives totally id1 + n - 1 - id2 steps. If id1 > id2, we need id1 + n - 1 - id2 - 1 steps, where the last term  - 1 comes from that when we move the maximum value to the head, the minimum value in fact has been moved one position to the right.

144B - Meeting

The solution is straightforward. We enumerate each point on the four sides, and check whether it is included by at least one circle or not. Note that the four corner points should be checked only once.

144C - Anagram Search

Let us denote the length of the first and second string as slen and plen (these strings are denoted as s and p). It is obvious that if slen < plen, then it is impossible to find any good substrings.

For slen ≥ plen, we only need consider the substrings of s with length plen. It is convenient to imagine that we have a sliding window and move along string s to find good substrings. For any substring of length plen, we use a hash table to store the number of letters that appear there. For simplicity, we use hs[i] and hp[i] to denote the number of letter 'i' appearing in string s and p, respectively. One can check that if for all letter 'i', we have hs[i] ≤ hp[i], then the current substring is good, since the “missing” letters can be obtained by replacing '?'. Otherwise, it is definitely not a good substring, since the “redundant” letters can not be eliminated.

Note that hp[i] can be calculated once for all while hs[i] should be updated whenever we move the sliding window one step forward, which can be implemented with complexity O(1) as only one old letter is removed and one new letter is added. Thus, the total complexity is O(max(slen, plen)).

144D - Missile Silos

The main solution contains two parts.

The first part is Dij algorithm based on priority queue, since the given graph is sparse. There are a large number of materials (also codes) describing the detailed implementation and thus omitted here.

For the second part, we should find out all the required points. At first, we check all the nodes and find out all those that have an exact distance l. Then, we enumerate each edge and check whether there exist positions on the edge that also have a distance l. It can be observed that there are at most two positions that have a chance to have a distance l. One is by passing one node while the other one is by passing the other node. Be careful that these two positions may coincide with each other.

144E - Competition

For a cell (r, c) that belongs to the secondary diagonal, it can only be reached from cells (i, j) that satisfy r ≤ i ≤ n and c ≤ j ≤ n, which in fact forms a rectangular.

We can enumerate the cells in the secondary diagonal from bottom to top and also maintain a set containing the candidate sportmans that can be selected. Initially, we check row n and only consider the sportmans that belong to row n. We select the sportman that has the minimum column index and if there are multiple such sportmans, we further select the one the minimum row index. Before we move to row n - 1, we should first delete the selected sportman, and then further delete all sportmans belonging to column 1 from the candidate set, while at the same time add the sportmans that belongs to row n - 1 to the set. Then, we move to row n - 1 and repeat the above operations again.

Generally speaking, when we try to find a sportman that should go to cell (r, c) which belongs to the secondary diognal, we should select one sportman from our candidate set (note that it might be empty), and then delete it and also delete all the sportmans that have a column index c while adding sportmans that have a row index r - 1, and then move to the upper row.

In fact this is a greedy algorithm and by some induction one can see that this will result in a reasonable answer. Now we prove that the complexity is O(mlog(m)).

Suppose that the number of sportmans in the i-th row is r_i while in the j-th column is c_j. When we are dealing with cell (i, n + 1 - i), we delete c_{n + 1 - i} sportmans while adding r_i - 1 sportmans. Both the deleting and adding operation can be implemented with complexity O(logm). Thus, the total number of deleting operations is 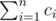and the total number of adding operations is 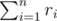, which gives .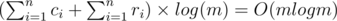