146A - Lucky Ticket

We read in the integer as a string and the left work is straightforward implementation.

146B - Lucky Mask

For a < b, the answer is obviously b. If a ≥ b, note that 10⁶ + b is always a potential answer except that it might not be the minimum one. Therefore, we can enumerate integers from a + 1 and immediately terminate the loop if we find the first integer that satisfies the requirement (the loop will surely be terminated since 10⁶ + b provides an upper bound).

146C - Lucky Conversion

Let us compare the two strings position by position, and denote the total number of indices which lead to difference as m. For the first string, its m indices must “contain” m₁ 4s and m₂ 7s, while for the second string, it becomes m₁ 7s and m₂ 4s. To achieve the minimum number of operations, we should swap min(m₁, m₂) 4s and 7s while changing the left max(m₁, m₂) - min(m₁, m₂) from 4s to 7s (or from 7s to 4s). Thus, the final answer is in fact max(m₁, m₂).

146D - Lucky Number 2

Let us first consider what happens when we try to write a sequence. Suppose that we write a 4 first. Then, no 47 or 74 appears until we write a 7 (since one can keep writing 4, which gives 444...). Right now, we have one 47 and zero 74. Next, no more 47 or 74 appears until we write a 4, and now we have one 47 and one 74. By some simple induction, one can find that we always have k 47s and k - 1 or k 74s, i.e., the number of 74s is either equal to that of 47s or one less than that of 47s. Similarly, if we write a 7 first, we either have one more 74 than 47 or equal number of 47s and 74s.

With the above arguments, no reasonable sequence exists if |a₃ - a₄| > 1. Thus, we can solve the problem based on the following three cases.

1) a₃ - a₄ = 1: the pattern must be like (44..444)(4747..47)(77..77). The middle '( )' contains a₃ 47s, while the left and right '( )' contains the remaining 4s and 7s. The reason is that if we insert more 4s into the middle '( )', it is still a reasonable sequence but not the minimum one (obviously we should put as many 4s in the front as possible). The reason is similar why we should not insert more 7s into the middle '( )'.

2) a₄ - a₃ = 1: the pattern should be like (77..777)(7474...7474)(44..44). The middle '( )' should have a₄ 74s and the remaining 7s and 4s are put into the left and right '( )', respectively.

3) a₃ = a₄: the pattern can be either (74)(44..44)(74..74)(77..77)(7) or (44..44)(4747..47)(77..77)(4). For the first one, the first '( )' contains exactly one 74, and the last '( )' should contain exactly one 7, and the third '( )' should contain a₄ - 1 74s, while the remaining 4s and 7s are inserted into the other two '( )'. For the second pattern, the last '( )' has exactly one 4, and the second '( )' has a₃ 47s while the remaining 4s and 7s are put into the other '( )'.

146E - Lucky Subsequence

This problem involves several wonderful techniques.

The main idea is to divide the given integers into two sets, one consisting of unlucky integers while the other one containing lucky integers. We use f(i) and g(i) to denote the number of different ways to select i and j integers from the two sets, respectively. Thus, to select totally k integers, we have 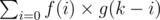ways.

Let us first consider how to compute f(i). It is obvious that f(i) is just equal to the conventional 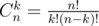. There is a standard algorithm to compute formula like 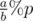. By using Fermat's theorem, we can transfer it into ab^p - 2%p. Furthermore, one can adopt fast exponentiation to calculate b^t%p (note that we can calculate all the values of n!%p in previous).

Then, we focus on how to compute g(i). Suppose that there are totally m different lucky integers and the number of the i-th lucky integer is denoted as num[i] (there may exist multiple same lucky integers). Then, we use dp[i][j] to denote the number of ways to choose j different lucky integers among the first i ones. The recursive formula is dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] × num[j], which is similar to pascal triangle, and thus g(i) = dp[m][i]. To obtain num[i], one should implement data compression first, since the data range is huge but the number of lucky integers is less than 1024.

As a summary, the involved techniques are prefix idea, fermat's theorem, fast exponetiation, dp and data compression. This is a delicately designed problem.

145E - Lucky Queries

I read the tutorials and learned an advanced version of segment tree there. One could find a large number of materials about various segment trees and their implementation, either on the internet, or in many blogs posted in codeforces. Here I recommend this solution 1115215, and I think the overall framework is written in a very clear, systematic and standard manner.