qoo2p5's blog

HourRank 25
By qoo2p5, 7 years ago, In English

Hello Codeforces Community!

Happy New Year to all!

I invite you all to join HackerRank's HourRank 25 on January 2, 2018, at 20:30 IST.

There will be three tasks in the round and one hour for you to solve them. The contest will be rated and the top ten contestants will receive HackerRank T-shirts!

The problems are prepared by me and tested by niyaznigmatul. Thanks to kevinsogo for help in setting up this contest.

I hope you’ll enjoy the problems.

Good luck and Happy Coding!

  • Vote: I like it
  • +67
  • Vote: I do not like it

Comments Comments (40)
| Write comment?
»
7 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Again same question http://codeforces.net/blog/entry/56314?#comment-400599.
Does Hackerrank exclude this people from winners' list and add first people with rank bigger than 10?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    afaik, they send the equivalent in money to the non-eligible countries

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -6 Vote: I do not like it

.

→ Reply
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

My hard passed after fixing stupid bug 1 minute after the contest ended :(

→ Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it +15 Vote: I do not like it

Let l[i] be the smallest such that a[i] ≥ a[k] for all l[i] ≤ k < i, r[i] be the largest such that a[i] > a[k], for all i < k ≤ r[i]. I guess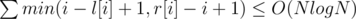 . Can one show me a proof or it is wrong?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I found it myself.

    Denote f(n) is the maximal sum for an array of length n. Consider the last largest element, one can easily see: f(n) = max(f(x) + f(y) + min(x + 1, y + 1)|x + y = n - 1).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I calculated this recurrence and found that it looks like . But do you have any ideas how to proof it?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +18 Vote: I do not like it

        f(n) is the maximal number of operations in the process "merge small to large subtree" on the binary tree of size n.

        → Reply
»
7 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Can someone discuss their approaches for The Strange Function ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Let's call "complete" segment a segment which gcd value would change if we would add number to the left of it or to the right of it. Total length of all complete segments is O(n log n), so we would just solve problem for each one of them

    Additionally for each element let's find maximal subarray where it is maximum.

    Now for each complete segment we would look at each element, look at intersection of complete segment and maximal subarray and we would need to find consecutive elements to the left of it within this intersection and also to the right of it. This is done using segment tree

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you give some more details. Also, it would be really kind, if you can attach the code.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How is the total length of all complete segments O(n log n) ?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        That's incorrect, yes. Best I can do is O(n log^2 (max(a))

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    There are quite a few possible approaches on this one :)

    Besides things already described here, I can add one more idea: "I see that N is very small for some unknown reason, most likely naive solution can get AC". Indeed, it took quite some time to make it work, but my solution from the contest is O(N2) brute.

    Also, at first I was lazy to code something similar to model solution and decided to code alternative one instead — let's fix left endpoint, consider all segments with this left endpoint and particular value of GCD and pick a position with largest prefix sum as a right endpoint. Midway I realized that it is wrong :) But it turns out tests are allowing this one to pass as well — you can check solution from the contest by natsugiri, which almost exactly matches my idea: code. The issue is: maximizing prefix sum doesn't always lead to maximizing (prefix sum minus max element) because it is possible to increase prefix sum a little bit while increasing max element much more. Here is a test for it:

    9
10 10 10 10 10 -30 20 -10 30

    Correct answer is 400 for taking [1,5], not 300 for taking [1,9].

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +4 Vote: I do not like it

My First Contest of 2018. Missed my First gold Badge by 10 ranks.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    My first contest of 2018, took me an hour ~20 minutes to realize I was using a[i] * fi[v/2] instead of (a[i] * fi[v/2])%md.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      haha, I made a wrong submission for that problem for not initializing f[0]=1 .

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you tell the badgewise rank distribution please?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it
      Click
      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Problem C,I assumed that the place j where F(i,j) is maximal for each 1<=i<=n is non-decreasing with the increasement of i and wrote a divide-and-conquer solution for it.However,it turned out it received Wrong Answer on a few testcases. Can anyone tell me why it's not correct?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    How do say its non decreasing. It is a combination of a decreasing function and another random function

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well,it's just my first sense after seeing the problem and I found it maybe reasonable,so I implemented it. And now I'm curious about on what kind of tests can it produce wrong answer.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it
        Try this
        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thank you!

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            And another question,if all ai is positive,will the conclusion hold?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Nope

              try this
              → Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Big win for Serbia :)

Congratulation ivan100sic !

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain the third problem? I do not understand it from the editorial.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    First of all consider gcd(al, al + 1, ..., at). For fixed l, this can only take different values (for gcd to decrease, it must be atleast half of the previous value, as it must properly divide the previous gcd). Also for each such value g, there is a range [ag, bg] such that the gcd is same (and equal to g) only for these values.

    Fix a l and take a g. Let its range be [a, b]. Now you need to maximize f(t) = al + ... + at - max(al, ..., at). Write this as hl(t) - pref[l - 1] where hl(t) = pref[t] - max(al, ..., at), where pref[i] = a1 + ... + ai. Since for given l, g it is sufficient to maximize hl(t) over [a, b], we will maintain this in a segment tree.

    Now suppose you have worked from n till l + 1, and have values of hl + 1(t) in the segtree. How do you update this to hl?

    pref[t]'s do not change. Consider a[l]. The max(al, ... at) part will be updated (to a[l]) for all j such that there is no other element greater than a[l] between [l, j]. All the others remain unchanged.

    Keep a stack, which stores elements in increasing order (popping elements if they are lesser than the current number), and for each element, stores the range, over which they are max. Also keep a segment tree which stores hl, and can support range update (addition), and range query(maximum)

    For example, for [4, 7, 5, 6], from the end, you first have 6, which is max from [4..4]. Then you get 5, which is less than 6, and is max from [3..3], so you stack looks like (top to end) [5, 6]. Next we get 7, which is greater than 5. So you pop 5, and since it was max from [3..3], you add (because the max is subtracted in hl) 5 to the range, and subtract the new max, 7. Then you get 6, and you also pop it, and do the same. The range for 7 becomes [2..4]. Finally you just add 4, with range [1..1].

    All this is done with a stack. Updates are done in segment tree, and you can enumerate all valid l, g pairs in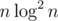 by binary search, and querying gcd over range. The complexity is thus (something like, point out if I miss terms) .

    → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

I had the solution for the 2nd problem but did not know how to do modulo division!

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

Three things are eternal:

  1. The universe
  2. while(1);
  3. Ratings will be updated soon, please wait!
→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How long does it take to update ratings on hackerrank? zzzz...

And I thought codeforces' rating update was slow...

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

@HackerRank , do you realise that among the platforms AtCoder, CF, CC, CSA, HR , yours is the slowest to update ratings ? !!

→ Reply