148A - Insomnia cure

A straightforward solution is to enumerate every element in the sequence and check whether it can divide at least one of the given four integers.

148B - Escape

We can simply simulate the process until the princess reaches the destinatiin. Be careful that when comparing two “double” types, it is better to use a < b + ε instead of directly checking a < b, where ε can be set to 1e - 9 (I used this value).

148C - Terse princess

A greedy algorithm can solve the problem. The first element can be assigned with value 1. Then, for the next b elements, we assign values so that each of them is larger than the sum of all the previous elements. For the next a elements, each of them should be larger than the maximum value of the previous elements. Finally, we can assign the remaining elements with the same value.

Note that there are two special cases which are quite tricky to a certain extent.

One case is that a = n - 1 (this has implied that b = 0 due to the constraint a + b < n). In fact, there exists no reasonable sequence since the second element must be larger than the first one, however this means that the second element should belong to type “b” rather than type “a” while b = 0 here.

The second case is b = 0, 0 < a < n - 1. A reasonable sequence exists for this case, but be careful to make sure that the second element should not be larger than the first one (same reason as mentioned above).

148D - Bag of mice

I used a classic probability model (I am not sure of the terminology...) to solve it.

Given n = b + w elements, there are totally n! permutation and we are going to find all the patterns that the princess wins. It is convenient to define the “first winning event”, i.e., the step at which the princess wins.

Note that the n elements can be divided into multiple groups, each of which consists of three elements (the last group may have less than three). The first winning event must be one of the following patterns, where “x” means that it can be either “w” or “b”.

wxx xxx xxx ...

bbx wxx xxx ...

bbx bbx wxx xxx ...

....

Suppose that we have g groups and the first “w” appears in the first element of the i-th group, and we are going to calculate its probability p(i). To form such a pattern, we have A_w¹ ways to select the first “w”, and A_b^2i - 2 ways to choose the previous “b”s, and finally (n - 1 - (2i - 2))! ways to deal with the remaining elements (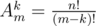). Thus, we have 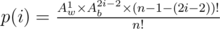. In general, it is better to transfer the formula to logarithm domain, i.e., we compute log(p(i)) instead. After some simple deduction, one can find that the main issue is reduced to the computation of log(k!) for some positive integer k. We can calculate it when necessary, which results in complexity of O(N²), or calculate in previous and maintain a table, which gives O(N).

148E - Porcelain

For the i-th shelf, we first consider given that we can select m_i elements, what is the maximum value that we can take. According to the problem, we could select x elements from left and y elements from right, with x + y = m_i. Thus, we can calculate prefix sum and suffix sum, and enumerate every feasible pair of (x, y) to find out the maximum value.

Then, the original problem is reduced to find max(f₁(m₁) + f₂(m₂) + ... + f_n(m_n)), given that m₁ + m₂ + ... + m_n = m, where f_i(m_i) denotes the maximum value given that we can select m_i elements from the i-th shelf.

The reduced problem can be solved based on dp. We use dp[i][j] to denote the maximum value that we can obtain under the condition that totally j elements have been selected from the first i shelves. The recursive formula is dp[i][j] = max_{mi = 0, 1, 2, ..}(dp[i - 1][j - m_i] + f(m_i)). The final answer is just dp[n][m].