genius_noob's blog

Cyclic Quadrilateral ?

By genius_noob, history, 7 years ago, In English

Can we always form a cyclic quadrilateral using 4 side lengths? I was solving this problem on SPOJ http://www.spoj.com/problems/QUADAREA/. In order to find the maximum area of quadrilateral with side lengths given, I applied Brahmagupta's formula K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}\, and i got AC. I am wondering, is that always possible? Is there any proof?

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Yes.

link

If you choose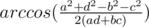 as an angle between a and d you choose 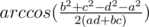as an angle between b and c, then you have cyclic quadrilateral.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    link

    using this, you can prove that it will be valid quadrilateral by finding diagonal using a and d and using b and c

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    But u can control only one angle at a time I guess, either between a and d or between b and c, provided a and d, b and c are adjacent.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, if you control an angle between a and d, then you know one diagonal, so then you can find an angle between b and c.

      If you choose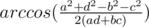 as an angel between a and d then the angle between b and c is .

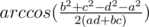      → Reply