Блог пользователя genius_noob

Cyclic Quadrilateral ?

Автор genius_noob, история, 7 лет назад, По-английски

Can we always form a cyclic quadrilateral using 4 side lengths? I was solving this problem on SPOJ http://www.spoj.com/problems/QUADAREA/. In order to find the maximum area of quadrilateral with side lengths given, I applied Brahmagupta's formula K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}\, and i got AC. I am wondering, is that always possible? Is there any proof?

  • Проголосовать: нравится
  • +2
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится +3 Проголосовать: не нравится

Yes.

link

If you choose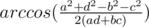 as an angle between a and d you choose 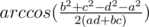as an angle between b and c, then you have cyclic quadrilateral.

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    link

    using this, you can prove that it will be valid quadrilateral by finding diagonal using a and d and using b and c

    → Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    But u can control only one angle at a time I guess, either between a and d or between b and c, provided a and d, b and c are adjacent.

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Yes, if you control an angle between a and d, then you know one diagonal, so then you can find an angle between b and c.

      If you choose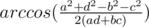 as an angel between a and d then the angle between b and c is .

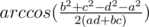      → Ответить