Recently I was trying to solve the problem Sum of MSLCM from ACM ICPC Live Archive.
After a little analysis, I found out that the answer is S — 1, where S is the sum of all X such that,
X = A * (int)(N / A) for all A in the range [1, N].
int ans=0
for(int a=1;a<=n;a++){
ans+=a*(int)(n/a);
}
But my solution won't pass the time limit if I iterate over the range [1, N] as N can be as large as 20000000.
I couldn't find another solution even after several hours of thinking and decided to search for the solution on the internet. While searching for the solution I found the following code.
#include <bits/stdc++.h>
using namespace std;
#define long long long int
int main()
{
ios_base::sync_with_stdio(false);
long n;
while(cin>> n && n){
long ans=0,a=1;
while(a<=n){
long x=n/a;
long y=n/x;
ans+=x*(((a+y)*(y-a+1))/2);
a=++y;
}
ans--;
cout<< ans <<endl;
}
return 0;
}
This solution passed the time limit for the given input range and got accepted.
But I still couldn't understand the formula used in this code. The only optimization I see here is that it doesn't iterate over all the numbers in the range [1, N]. But how does that work?
I want a mathematical explanation of this solution.










Let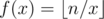 , 1 ≤ x ≤ n. Let's find out how many distinct values the function can get by dividing it in two cases.
, 1 ≤ x ≤ n. Let's find out how many distinct values the function can get by dividing it in two cases.
Case 1: If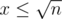 , f can get at most
, f can get at most  distinct values.
distinct values.
Case 2: If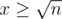 , n / x is always less than or equal to
, n / x is always less than or equal to  .
.
Therefore, f can get at most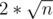 distinct values. We can find the values and count their appearances in
distinct values. We can find the values and count their appearances in  time, which allows us to compute the sum efficiently.
time, which allows us to compute the sum efficiently.
Well understood. thanks a lot.
I know this is not the expected solution, but it can be solved in O(n·log n) time and O(n) memory. Doing a preprocessing with n = 2·107 and with O(1) queries the execution time is almost five seconds on the server, but it still passes.
I tried preprocessing to answer each query in O(1) time, but couldn't. Can you explain in detail how it can be done?
You can apply a sieve, suppose S[i] = Sum of Divisors of i.
For every number i in [1..107] we add i to its multiples (2i, 3i, 4i,...)
Then, we apply a preffix sum (S[i] = S[i] + S[i - 1]).
This preprocessing has a complexity of O(n·log n) where n is the maximum number in the tests. The constraints state that 2 ≤ n ≤ 107
Again, this is not the expected solution, and I think it's not even a good one!
Got this. It's not the fastest solution, but it may pass the time limit I think.