Tutorial is loading...
Code
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;
cin>>s;
cout<<s;
reverse(s.begin(),s.end());
cout<<s;
return 0;
}
Tutorial is loading...
Code
#include "bits/stdc++.h"
#ifdef PRINTERS
#include "printers.hpp"
using namespace printers;
#define tr(a) cerr<<#a<<" : "<<a<<endl
#else
#define tr(a)
#endif
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
int x[10][1000005];
int f(int x){
if(x<10)return x;
int prod=1;
while(x){
if(x%10)prod*=(x%10);
x/=10;
}
return f(prod);
}
void solve(){
for(int i=1;i<=1000000;i++){
x[f(i)][i]++;
}
for(int i=1;i<10;i++){
for(int j=1;j<=1000000;j++){
x[i][j]+=x[i][j-1];
}
}
int Q;
cin>>Q;
while(Q--){
int l,r,k;
cin>>l>>r>>k;
cout<<x[k][r]-x[k][l-1]<<endl;
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
Tutorial is loading...
Code
#include "bits/stdc++.h"
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
void solve(){
int n,a,b;
cin>>n>>a>>b;
vector<int>v(n);
iota(all(v),1);
int i=0;
while(i<n){
if((n-i)%b==0){
if(b>1)rotate(v.begin()+i,v.begin()+i+1,v.begin()+i+b);
i+=b;
}
else{
if(i+a>n){
cout<<-1;
return;
}
if(a>1)rotate(v.begin()+i,v.begin()+i+1,v.begin()+i+a);
i+=a;
}
}
for(auto j:v)cout<<j<<" ";
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
Tutorial is loading...
Thanks to radoslav11 for nice and short editorial in comments.
Code
#include "bits/stdc++.h"
#ifdef PRINTERS
#include "printers.hpp"
using namespace printers;
#define tr(a) cerr<<#a<<" : "<<a<<endl
#else
#define tr(a)
#endif
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
int par[20][400000];
ll par_sum[20][400000];
int w[400000];
void solve(){
int Q;
cin>>Q;
w[0]=INT_MAX;
int last=0;
int cur=1;
for(int i=0;i<20;i++)par_sum[i][1]=1e16;
while(Q--){
int ch;
cin>>ch;
if(ch==1){
ll p,q;
cin>>p>>q;
p^=last;
q^=last;
cur++;
w[cur]=q;
if(w[p]>=w[cur]){
par[0][cur]=p;
}
else{
int from=p;
for(int i=19;i>=0;i--){
if(w[par[i][from]]<w[cur])
from=par[i][from];
}
par[0][cur]=par[0][from];
}
par_sum[0][cur]=(par[0][cur]==0?1e16:w[par[0][cur]]);
for(int i=1;i<20;i++){
par[i][cur]=par[i-1][par[i-1][cur]];
par_sum[i][cur]=(par[i][cur]==0?1e16:par_sum[i-1][cur]+par_sum[i-1][par[i-1][cur]]);
}
}
else{
ll p,q;
cin>>p>>q;
p^=last;
q^=last;
if(w[p]>q){
cout<<0<<endl;
last=0;
}
else{
q-=w[p];
int ans=1;
for(int i=19;i>=0;i--){
if(par_sum[i][p]<=q){
ans+=(1<<i);
q-=par_sum[i][p];
p=par[i][p];
}
}
cout<<ans<<endl;
last=ans;
}
}
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
Tutorial is loading...
Code
#include "bits/stdc++.h"
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
int dp[5001][5001];
ll expo(ll base, ll exponent, ll mod) {
ll ans = 1;
while(exponent !=0 ) {
if((exponent&1) == 1) {
ans = ans*base ;
ans = ans%mod;
}
base = base*base;
base %= mod;
exponent>>= 1;
}
return ans%mod;
}
int fill(int diffs,int a,int tot){
if(dp[diffs][a]>=0)return dp[diffs][a];
int b=tot-a;
if(diffs==0){
return dp[diffs][a]=expo(2,b,hell);
}
return dp[diffs][a]=((b?1LL*b*fill(diffs-1,a+1,tot):0LL)+(a?1LL*a*fill(diffs-1,a,tot):0LL))%hell;
}
void solve(){
int N,k;
cin>>N>>k;
memset(dp,-1,sizeof dp);
cout<<fill(k,0,N)<<endl;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
Tutorial is loading...
Code
#include "bits/stdc++.h"
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;i++)
using namespace std;
bool Q;
struct Line {
mutable ll k, m, p;
bool operator<(const Line& o) const {
return Q ? p < o.p : k < o.k;
}
};
struct LineContainer : multiset<Line> {
const ll inf = LLONG_MAX;
ll div(ll a, ll b){
return a / b - ((a ^ b) < 0 && a % b);
}
bool isect(iterator x, iterator y) {
if (y == end()) { x->p = inf; return false; }
if (x->k == y->k) x->p = x->m > y->m ? inf : -inf;
else x->p = div(y->m - x->m, x->k - y->k);
return x->p >= y->p;
}
void add(ll k, ll m) {
auto z = insert({k, m, 0}), y = z++, x = y;
while (isect(y, z)) z = erase(z);
if (x != begin() && isect(--x, y)) isect(x, y = erase(y));
while ((y = x) != begin() && (--x)->p >= y->p)
isect(x, erase(y));
}
ll query(ll x) {
assert(!empty());
Q = 1; auto l = *lower_bound({0,0,x}); Q = 0;
return l.k * x + l.m;
}
};
vector<int> x,y;
vector<vi> adj;
vector<ll> ans;
vector<int> subsize;
void dfs1(int u,int v){
subsize[u]=1;
for(auto i:adj[u]){
if(i==v)continue;
dfs1(i,u);
subsize[u]+=subsize[i];
}
}
void dfs2(int v, int p,LineContainer& cur){
int mx=-1,bigChild=-1;
bool leaf=1;
for(auto u:adj[v]){
if(u!=p and subsize[u]>mx){
mx=subsize[u];
bigChild=u;
leaf=0;
}
}
if(bigChild!=-1){
dfs2(bigChild,v,cur);
}
for(auto u:adj[v]){
if(u!=p and u!=bigChild){
LineContainer temp;
dfs2(u,v,temp);
for(auto i:temp){
cur.add(i.k,i.m);
}
}
}
if(!leaf)ans[v]=-cur.query(x[v]);
else ans[v]=0;
cur.add(-y[v],-ans[v]);
}
void solve(){
int n;
cin>>n;
x.resize(n+1);
y.resize(n+1);
ans.resize(n+1);
subsize.resize(n+1);
adj.resize(n+1);
rep(i,1,n+1)cin>>x[i];
rep(i,1,n+1)cin>>y[i];
rep(i,1,n){
int u,v;
cin>>u>>v;
adj[u].pb(v);
adj[v].pb(u);
}
dfs1(1,0);
LineContainer lc;
dfs2(1,0,lc);
rep(i,1,n+1)cout<<ans[i]<<" ";
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
solve();
}
return 0;
}
Tutorial is loading...
Code 1
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define vi vector<int>
#define all(a) (a).begin(),(a).end()
#define F first
#define S second
#define sz(x) (int)x.size()
#define hell 1000000007
#define endl '\n'
using namespace std;
const int MAXN=1000005;
string s;
struct PalindromicTree{
int N,cur;
vector<map<int,int>> next;
vector<int> link,start,len,diff,slink;
PalindromicTree(): N(0),cur(0){
node();
len[0]=-1;
node();
}
int node(){
next.emplace_back();
link.emplace_back(0);
start.emplace_back(0);
len.emplace_back(0);
diff.emplace_back(0);
slink.emplace_back(0);
return N++;
}
void add_letter(int idx){
while(true){
if(idx-len[cur]-1>=0 && s[idx-len[cur]-1]==s[idx])
break;
cur=link[cur];
}
if(next[cur].find(s[idx])!=next[cur].end()){
cur=next[cur][s[idx]];
return;
}
node();
next[cur][s[idx]]=N-1;
len[N-1]=len[cur]+2;
start[N-1]=idx-len[N-1]+1;
if(len[N-1]==1){
link[N-1]=diff[N-1]=slink[N-1]=1;
cur=N-1;
return;
}
while(true){
cur=link[cur];
if(idx-len[cur]-1>=0 && s[idx-len[cur]-1]==s[idx])
break;
}
link[N-1]=next[cur][s[idx]];
diff[N-1]=len[N-1]-len[link[N-1]];
if(diff[N-1]==diff[link[N-1]])
slink[N-1]=slink[link[N-1]];
else
slink[N-1]=link[N-1];
cur=N-1;
}
};
ll dp[MAXN],sans[MAXN];
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
PalindromicTree pt;
int i,cur;
string str;
cin>>str;
for(i=0;i<sz(str)/2;i++){
s.pb(str[i]);
s.pb(str[sz(str)-i-1]);
}
dp[0]=1;
for(i=1;i<=sz(s);i++){
pt.add_letter(i-1);
for(cur=pt.cur;cur>1;cur=pt.slink[cur]){
sans[cur]=dp[i-pt.len[pt.slink[cur]]-pt.diff[cur]];
if(pt.diff[cur]==pt.diff[pt.link[cur]])
sans[cur]=(sans[cur]+sans[pt.link[cur]])%hell;
dp[i]=(dp[i]+sans[cur])%hell;
}
if(i&1)
dp[i]=0;
}
cout<<dp[sz(s)];
return 0;
}
Code 2
#define NDEBUG
NDEBUG
#include <algorithm>
#include <array>
#include <bitset>
#include <cassert>
#include <cstring>
#include <cmath>
#include <functional>
#include <iomanip>
#include <iostream>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <tuple>
#include <unordered_map>
#include <unordered_set>
#include <vector>
#include <memory>
#include <queue>
#include <random>
#define forn(t, i, n) for (t i = 0; i < (n); ++i)
using namespace std;
// TC_REMOVE_BEGIN
/// caide keep
bool __hack = std::ios::sync_with_stdio(false);
/// caide keep
auto __hack1 = cin.tie(nullptr);
// TC_REMOVE_END
// Section with adoption of array and vector algorithms.
#define ENABLE_IF(e) typename enable_if<e>::type* = nullptr
namespace template_util {
constexpr int bytecount(uint64_t x) {
return x ? 1 + bytecount(x >> 8) : 0;
}
template<int N>
struct bytetype {
};
template<>
struct bytetype<4> {
typedef uint32_t type;
};
template<>
struct bytetype<1> {
typedef uint8_t type;
};
/// caide keep
template<uint64_t N>
struct minimal_uint : bytetype<bytecount(N)> {
};
}
template<class T>
T next(istream& in) {
T ret;
in >> ret;
return ret;
}
/*
TODOs:
primitive root
discrete log
tests!!!
*/
namespace mod_impl {
/// caide keep
template <class T>
constexpr inline T mod(T MOD) {
return MOD;
}
/// caide keep
template <class T>
constexpr inline T mod(T* MOD) {
return *MOD;
}
/// caide keep
template <class T>
constexpr inline T max_mod(T MOD) {
return MOD - 1;
}
/// caide keep
template <class T>
constexpr inline T max_mod(T*) {
return numeric_limits<T>::max() - 1;
}
constexpr inline uint64_t combine_max_sum(uint64_t a, uint64_t b) {
return a > ~b ? 0 : a + b;
}
/// caide keep
template <class T>
constexpr inline uint64_t next_divisible(T mod, uint64_t max) {
return max % mod == 0 ? max : combine_max_sum(max, mod - max % mod);
}
/// caide keep
template <class T>
constexpr inline uint64_t next_divisible(T*, uint64_t) {
return 0;
}
//caide keep
constexpr int IF_THRESHOLD = 2;
template <class T, T MOD_VALUE, uint64_t MAX,
class RET = typename template_util::minimal_uint<max_mod(MOD_VALUE)>::type,
ENABLE_IF(MAX <= max_mod(MOD_VALUE) && !is_pointer<T>::value)>
inline RET smart_mod(typename template_util::minimal_uint<MAX>::type value) {
return value;
}
template <class T, T MOD_VALUE, uint64_t MAX,
class RET = typename template_util::minimal_uint<max_mod(MOD_VALUE)>::type,
ENABLE_IF(max_mod(MOD_VALUE) < MAX && MAX <= IF_THRESHOLD * max_mod(MOD_VALUE) && !is_pointer<T>::value)>
inline RET smart_mod(typename template_util::minimal_uint<MAX>::type value) {
while (value >= mod(MOD_VALUE)) {
value -= mod(MOD_VALUE);
}
return (RET)value;
}
}
#define MAX_MOD mod_impl::max_mod(MOD_VALUE)
struct DenormTag {};
template <class T, T MOD_VALUE, uint64_t MAX = MAX_MOD, ENABLE_IF(MAX_MOD >= 2)>
struct ModVal {
typedef typename template_util::minimal_uint<MAX>::type storage;
storage value;
/// caide keep
inline ModVal(): value(0) {
assert(MOD >= 2);
}
inline ModVal(storage v, DenormTag): value(v) {
assert(MOD >= 2);
assert(v <= MAX);
};
inline operator ModVal<T, MOD_VALUE>() {
return {v(), DenormTag()};
};
typename template_util::minimal_uint<mod_impl::max_mod(MOD_VALUE)>::type v() const {
return mod_impl::smart_mod<T, MOD_VALUE, MAX>(value);
}
};
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2,
uint64_t NEW_MAX = mod_impl::combine_max_sum(MAX1, MAX2),
ENABLE_IF(NEW_MAX != 0), class Ret = ModVal<T, MOD_VALUE, NEW_MAX>>
inline Ret operator+(ModVal<T, MOD_VALUE, MAX1> o1, ModVal<T, MOD_VALUE, MAX2> o2) {
return {typename Ret::storage(typename Ret::storage() + o1.value + o2.value), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX>
inline ModVal<T, MOD_VALUE>& operator+=(ModVal<T, MOD_VALUE>& lhs, const ModVal<T, MOD_VALUE, MAX>& rhs) {
lhs = lhs + rhs;
return lhs;
}
template <class T, T MOD_VALUE, class MOD_TYPE>
struct ModCompanion {
typedef MOD_TYPE mod_type;
typedef ModVal<mod_type, MOD_VALUE> type;
template <uint64_t C>
inline static constexpr ModVal<mod_type, MOD_VALUE, C> c() {
return {C, DenormTag()};
};
};
#undef MAX_MOD
template <uint64_t MOD_VALUE>
struct Mod : ModCompanion<uint64_t, MOD_VALUE, typename template_util::minimal_uint<MOD_VALUE>::type> {
template<uint64_t VAL>
static constexpr uint64_t literal_builder() {
return VAL;
}
template<uint64_t VAL, char DIGIT, char... REST>
static constexpr uint64_t literal_builder() {
return literal_builder<(10 * VAL + DIGIT - '0') % MOD_VALUE, REST...>();
}
};
#define REGISTER_MOD_LITERAL(mod, suffix) \
template <char... DIGITS> mod::type operator "" _##suffix() { \
return mod::c<mod::literal_builder<0, DIGITS...>()>(); \
}
template <class T, T MOD_VALUE, uint64_t MAX>
inline ostream& operator<<(ostream& s, ModVal<T, MOD_VALUE, MAX> val) {
s << val.v();
return s;
}
using md = Mod<1000000007>;
using mt = md::type;
REGISTER_MOD_LITERAL(md, mod)
struct Triple {
int start, delta, count;
int end() {
return start + delta * (count - 1);
}
};
// ostream& operator<<(ostream& out, const Triple& t) {
// out << "(" << t.start << ", " << t.delta << ", " << t.count << ")";
// return out;
// }
void solve(istream& in, ostream& out) {
auto s = next<string>(in);
string s1;
s1.reserve(2 * s.length());
forn (int, i, s.length() / 2) {
s1.push_back(s[i]);
s1.push_back(s[s.length() - i - 1]);
}
int n = s1.length();
vector<Triple> g;
vector<mt> d(n + 1), cache(n + 1);
d[0] = 1_mod;
forn (int, i, n) {
vector<Triple> g1;
int prev = -i - 1;
auto push = [&](Triple t) {
if (g1.empty() || t.delta != g1.back().delta) {
g1.push_back(t);
} else {
g1.back().count += t.count;
}
};
for (auto t : g) {
if (t.start > 0 && s1[t.start - 1] == s1[i]) {
t.start--;
if (prev != t.start - t.delta) {
push(Triple{t.start, t.start - prev, 1});
t.start += t.delta;
t.count--;
}
if (t.count > 0) {
push(t);
}
prev = t.end();
}
}
if (i >= 1 && s1[i - 1] == s1[i]) {
push(Triple{i - 1, i - 1 - prev, 1});
}
g = move(g1);
for (auto& t : g) {
mt add = d[t.end()];
if (t.count > 1) {
add += cache[t.start - t.delta];
}
if (t.start - t.delta >= 0) {
cache[t.start - t.delta] = add;
}
d[i + 1] += add;
}
}
out << d[n] << endl;
}
int main() {
solve(cin, cout);
return 0;
}











dynamic programming everywhere
Alternate solution for E.
Notice that the differentiation idea gives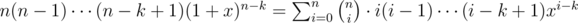 .
.
This motivates the idea to write xk as a sum of polynomials x, x(x - 1), x(x - 1)(x - 2), ... and x(x - 1)... (x - k + 1).
The coefficients for this linear combination is known to be the Stirling Numbers of the Second Kind. (you can also just calculate them) So combine that to have a O(K2) solution.
I get the differentiation part, but after that, I'm loosing on x^k as a sum of polynomials and Stirling numbers. Can you elaborate a bit!
If our goal was to solve for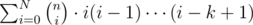 , we would be done by our first observation.
, we would be done by our first observation.
However, we are to solve for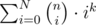 .
.
Therefore, it makes sense that we should try to write ik as a sum of i, i(i - 1), etc.
After that, we can use our first observation to collect the sum quickly.
About the part about Stirling Numbers, it isn't really needed (you can just calculate them directly) but it's the first equation in https://en.wikipedia.org/wiki/Stirling_numbers_of_the_second_kind#Generating_functions.
Here, (x)k = x(x - 1)... (x - k + 1). Hope you understand now.
If you know at least something about convex hull trick and have some prewritten code of it than you can easily solve problem F in not more than 10 minutes. IMHO this problem is very straightforward.
In Problem C P[j] = j-1 for i < j <= i+k-1 if I'm not wrong.
Fixed. Thanks. :)
In problem E : (1 + x)^n = sum, the sum should start from 0, not from 1.
Fixed. Thanks.
Another alternative solution for E:
Let's give xk a combinatorial meaning. xk is the number of combinations of picking k people from the subset with x people with repetition. For each subset we count all combinations and sum those.
Why not switch sums? For each combination we count the number of subsets in which the combination appears, and sum those. This obviously computes the same result.
Assume we have a combination of size k consisting of i distinct people. From which subsets can we construct this combination? Obviously the i people have to be in the subset, but for every other person we have two choices: he is in the subset or he isn't. It doesn't matter. Therefore there are 2n - i such subsets.
Let dp[j][i] be the number of combinations of size j with i distinct people, then the result is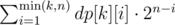 . dp[j][i] can be computed very easily with, you guess it, dynamic programming.
. dp[j][i] can be computed very easily with, you guess it, dynamic programming.
My submission: 35317193
Hello Jakube. Can you tell me why this way is wrong[ Written the steps in the picture provided in the link] . And why step 4 in the picture is not the general solution?
The differentials are wrong. You need to use the product rule!
Thanks. I got the mistake now. By the way in your explanation how you are calculating dp[i][j]. I mean the recurrence formula you are using to calculate it how it equal to dp[i][j].
Look in my submission. It is pretty basic: either the last element already appeared in the combination or it is new.
could you tell me why is (j * dp[i-1][j] + (n-j+1) * dp[i-1][j-1])?what is the combinatorial meaning? thank a lot!!!
To generate a combination with i elements from which j are distinct we have two options.
this part is clear now, but I dont understand how to deal with x^k yet
xk are just a bunch of combinations. And each one of those I count independently. This way I don't have to use xk in any of my computations.
How to count independently ? by a combination of size k consisting of i distinct people?
A so nice approach Jakube. Thanks.
TooDumbToWin please answer this question::
It came to my mind during the contest, corrrect me please: I thought that the answer will be always P=[1 2 3 ... n] . Suppose x = min(A,B), so in x moves this permutation will always satisfy both function f and g.
For your permutation, g(i) = 1 for all i. (Since x may not be 1, the permutation is wrong.)
Can someone explain D in a bit more detail?
In problem D, if every node in the sequence is a descendants of its predecessor,can it be solved?
It can be solved with a link cut tree
Another solution for problem E;
The last algebraic is easy for calculating.
In the fourth equation,why it is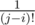 ?
?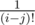 ?
?
Why not
Opps, thanks. Fixed
And also the seventh equation,there should be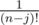 at last. :D
at last. :D
Thank you very much for this awesome solution.
( Sorry, my English is poor )
Another solution for E:
It can be proved (by mathematical induction) that ans(n, k) = 2n * fk(n), where fk(n) is a k-degree polynomial.
So we can use fk(0), fk(1)...fk(k) to calculate fk(n) with Lagrange interpolation method. ( Since we use consecutive integer as interpolation points, the interpolation will be very fast )
fk(0), fk(1)...fk(k) can be computed by simple O(k2) dp, or other O(k2) algorithms.
( But I got a WA on test 22, :( ) ( UPD: I forgot
%modsomewhere :( )Another (one more XD) solution for E:
The expression is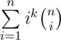
But you can also look at it as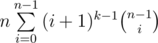
Which is kinda alike the original expression but taking k-1 instead of k and "shifting" the coefficients.
Let dp(k, j) be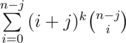 , so k means the current power and j means "how much have we shifted", and since we cannot shift more than k times then there are O(k2) different states. Note that our answer is n*dp(k,1). We have the following recurrence:
, so k means the current power and j means "how much have we shifted", and since we cannot shift more than k times then there are O(k2) different states. Note that our answer is n*dp(k,1). We have the following recurrence:
And then we have dp(k, j) = (n - j).dp(k - 1, j + 1) + j.dp(k - 1, j). Our base case is k=0, since that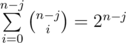 .
.
Very nice solution! I found the shifting idea first but couldn't make my DP work fast enough. I only had a O(k3) solution with O(k2) states. After that, I got the Stirling solution. It's nice to see that my failed approach could lead to such a wonderful solution :D
Can someone please explain Convex Hull on Tree in Task F in more details? How do we add new lines to the ancestors? Also, is it possible not to sort lines in CVH? Because recently I saw a task where lines were not sorted, but in editorial it was written that we have to use Convex Hull trick. Thanks!
You can use a set or linked list.When adding new lines,for set just insert,for linked list you need binary search.
After inserted lines,check the precursors and succeeds to maintain the CVH.
Sure, but how do we erase useless lines in the set when we add new lines?
F is solvable without the Merge Small to Large trick. We linearise the tree by Euler tour and then each subtree will represent a range in the tour. Then build a segment tree on it where each node will contain a CHT for the lines in its range. Initially the tree is empty, we can add lines on the go. Time complexity should be same.
How do you deal with the fact that the $$$a_x$$$ won't necessarily be sorted in each subtree?
Edit: never mind, I misunderstood it.
Maybe I can't read english straight right now, but I'm really confused on D condition 2:
Every node in the sequence is an ancestor of its predecessor.So... it's an ancestor of it's ancestor??? It's an ancestor of itself???
I think they mean "Every next node in the sequence".
If the sequence of nodes is denoted by {ai}, then ai + 1 is ancestor of ai.
Nice B, C, D — simple ideas for solutions was hidden under deterrent (a bit) statement.
The tutorial of E is AWESOME!!!
Can someone elaborate more on problem D?
I am quite new to the concept of binary lifting and I believe more people are in my situation.
Let's imagine you already have computed nxt[].
Now for the binary lifting, you keep an array jump[u][i] which shows the vertex in which you will be if you do nxt[nxt[nxt[...nxt[u]...]]] exactly 2i times.
Obviously jump[u][0] = nxt[u]. Well you can find that jump[u][i] = jump[jump[u][i - 1]][i - 1]. This way we can compute the jump values of a vertex in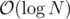 .
.
In a similar way, we will store sum[u][i], which is the sum of weights of the vertices, on the nxt[] path of length 2i (without jump[u][i]).
Now to answer the queries Let's find the highest ancestor in the jump array of vertex R, such that the sum on the path is less than or equal to X. This is obviously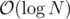 — we simply go through the array jump[R]. Lets call the cell which we found jump[R][j]. Now we add 2j to the answer, and remove sum[R][j]. We also move R to jump[R][j]. Well now we simply need to perform a query on these new R and X.
— we simply go through the array jump[R]. Lets call the cell which we found jump[R][j]. Now we add 2j to the answer, and remove sum[R][j]. We also move R to jump[R][j]. Well now we simply need to perform a query on these new R and X.
Obviously the length of the query chain is at most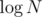 , so the complexity for each query will become
, so the complexity for each query will become 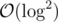 . You can notice that after each query the j decreases and achieve
. You can notice that after each query the j decreases and achieve 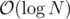 .
.
You are given N , A , B find such x and y that (A*x + B*y) = N .
If such x , y does not exist print -1 , either print x and y in same line separated by space , if there are multiple x , y that satisfy the equation print any of them .
For example: If N=9 , A=2 , B=5
then ans is 2 1 . Because 2*2+5*1=9 . Here A=2 , x=2 and B=5 , y=1 .
Constraint:
1<= N , A , B <= 10^18
INPUT
9 2 5
22 3 7
439365 78717 87873
505383 77277 99291
1000000 3 999997
474441 99291 77277
911106 51038 78188
321361 79845 81826
1000000000000000000 8765433 54343345
OUTPUT
2 1
5 1
0 5
-1
1 1
4 1
1 11
3 1
25359400 18397426840
I have solved using linear loop .
for(long long i=0; i<=n/a; i++) if((n-i*a)%b==0) { printf("%lld %lld\n",i,(n-i*a)/b); return 0; } printf("-1\n");But constraint is so big so this would not pass . For this test case n=1000000000000000000 , a=3 , b=798877665 code is getting TLE .
How to solve this problem efficiently ? This is a subproblem of this problem http://codeforces.net/contest/932/problem/C
https://en.wikipedia.org/wiki/Extended_Euclidean_algorithm
But extended eucleidean algorithm will work only when A*x+B*y=GCD(A,B) . That means N (variable of above problem) should have to be GCD(A,B) . But in this problem it is not guaranteed that N will always be gcd(A,B) .
https://www.math.uh.edu/~minru/number/hj02cs01.pdf
Can someone explain the code of problem B in more detail or suggest any related tutorial ?
Let di = a1 + a2 + ... + ai (in other words, di = di - 1 + ai). Then, al + al + 1 + ... + ar = dr - dl - 1.
RECURSIVE QUERIES And as 1 ≤ g(n) ≤ 9, using partial sum arrays for each possible value of g(n), we can answer the queries in O(1) explain this thing plzz how to use partial sum arrays and where did the author use this technique in its programme
x[i][j] is the count of numbers between 1 and j such that the value of g is i. So, each query can be answered as x[k][r] - x[k][l - 1].
did u actually use dp technique in your programme i am not able to see it
No, it's not DP. Try running the code using pen/paper on some small test cases. That might help. You can learn more about partial sums here.
then we can use bottom up dp for calculating g(n) for all the integers 1 ≤ n ≤ 10^6 in O(n).
:/
howz the time for calulating the g(n) is O(n).
Let us consider
If i analyse this for running time complexity then it should be till the number not reduces to single digit every time (loop for non zero digit product calculation runs from right to left that is over whole width of the no)..
Generally for any large number it no more then takes 4 to 5 compressions
then my time taken (4 or 5)*(width of the newly arrived no every time till the ans returned by the f(n) is not a single digit)..
How the time taken to find g(n) is O(n) here .. and n is the no So ur code want to say time is O(200140) if consider my case then plzz clear it !!
It is time complexity to calculate g(i) for i ≤ n using DP.
How would you go about solving A if you had to find the string of minimum length (which satisfies the given properties)?
try to iterate over possible centers of the palindrome. In basic version it takes O(n) to verify and find answer for a center. But using hashing we can verify and find ans for center in O(logn). So we can solve it for 1e5 length also.
Though there might be ways to get around hashing.
You can also use palindromic trees : 35425210
Can someone elaborate more on problem F?
The tutorial says that "Thus, convex hull trick of dp optimization can be used to find the minimum value. Once the value is calculated for a node, a line with slope b[i] and y-intercept dp[i] is added to the hull."
Does it mean that we treat every line as a point (b[i], dp[i]) and maintain the dynamic convex hull when we insert the point? If so, why?
THX.
Can anyone explain how next[] array is calculated in problem D? I am not able to understand from editorial.
I’m so sorry that I missed this post and the abundance of solutions to problem E, (possibly one of the greatest realizations of mathematics and computer science combined this year), so here I am with yet ANOTHER solution to problem E:
Make the “educated guess” that the solution is of form ansn = 2n * P(n), where P(n) is a polynomial of degree at most k + 5 over ZMOD (the + 5 part might be optimized out in future iterations, but let’s be honest to ourselves; we don’t care that much, do we?)
Gather some small answers (i.e. by the brute-force technique) and interpolate to find P
Bonus: can you find how I managed to make the educated guess about the form of the solution?
Seriously now, since when did I start to get the notion that combinatorics and formula calculations are not what competitive programming’s all about?
Problem F. Weak tests. Solutions that take into account only 30 vertices deeper than current get AC. http://codeforces.net/contest/932/submission/35515087
Yes I also use O(brute_force) and get AC,and I'm also curious if my code can be
changlleged admin please add more tests...
Here is a test which is not passed by both your and my solutions: https://drive.google.com/open?id=1f14u7zAiGKol_HQIOxjb9jWlttGumocQ
seems my answer is correct -10 100000 times...except for one zero on leaf
btw I think it is not easy to cha my code both deep<=20 and deep<=200
No, this is not correct. For the first 33333 vertices answer is -30, for the next 33333 vertices answer is -20, for the next 33332 vertices answer is -10, and the last one is 0. There are 3 vertices with "B" equal to -1: leaf of the tree and two more vertices with depth 33333 and 66666. So your solution gives WA for this test.
oh,I didn't notice three -1s ,but I can modify my algo a bit
when update dp[id], choose there children as candidate point bfs 200 distance,and choose children's decision node
and perform bfs 200 distance, how to cha it..
You can try to make your modifications, submit it and, I will try to challenge it tomorrow )
this is my new submissions it can pass the test you gave:
http://codeforces.net/contest/932/submission/35550022
test13 from this folder https://drive.google.com/open?id=1CGDePAKpdm8CTLEgQ2LJd9S_0imsF5QJ
another approach to E:
we can see that after each step of differentiation and multiplying it by 'x' we have the polynomial like xi * (1 + x)^(n - i). So, we can use normal differentiation rule for differentiating such polynomial and add it to the next step and after we have done we just put x = 1 and our answer is the sum of (2i * dp[k][i]) as xi = 1 for x = 1. here dp[k][j] denotes the co-efficient of the expression xi * (1 + x)^(n - i) after differentiating it k times.
what does the line "struct LineContainer : multiset{....}" do?
It means that the LineContainer inherits multiset
There's another way to reduce G to counting palindromic partitions. Consider a greedy palindromic partition of the string $$$s$$$ — by greedy, I mean the partition which takes the smallest suffix-prefix of $$$s$$$ and removes it from the beginning and the end of $$$s$$$. This is also known to be the partition with the maximum number of elements — see problem "Palindromic Partitions" from CEOI 2017. Take the first half of the partition and to each string in it assign a unique label. For example, for
ab|b|ab|ab|ab|ab|b|abremove the second halfab|b|ab|aband assign $$$x$$$ to $$$ab$$$ and $$$y$$$ to $$$b$$$. The solution is the number of palindromic partitions of the resulting string, in this casexyxx. Note that now we're counting all palindromic partitions, not just those where the lengths of palindromes are even.I understood $$$E$$$ but can someone help me in understanding why the operation we are considering is 'differentiate-and-multiply' rather than just 'differentiate'. Simple $$$k$$$-differentiation would be enough to get $$$i^k$$$ as the coefficient.
After differentiation, the power reduces by 1, so if not multiplied by x, next time differentiating multiplies the coefficient by (i-1) instead of i. So, you'd get i*(i-1)..(i-k+1) instead of i^k.
Ah, thanks.
Another issue is that we will lose a term each time if we just differentiate.
Thanks for your explanation :)
In problem C, I am not able to prove that if there does not exist non-negative integers x and y such that Ax+By=N, then it is not possible to construct such a permutation. Please help.
First of all i will prove that for any f(i, j) = i, a cycle of length j will be establised in which each of its element will follow the above rule and if above condition fails and remaining elements are left of length not A or B, then g(i) is either A or B will fail, let's say you found either of the sequence which follows g(i) = A, if you start with any other of link in this cycle like if you start calculating f(p[i], j), you will eventually get to p[i] because f(p[i], j-1) was i and f(i, 1) will be p[i], thus now you can see that if you find any j such that f(i, j) = i, then a cycle has been established of length j between all elements that were traversed until f(i, j) reduced to i, that's why u need 2 non-negative integers x and y which fulfill Ax + By = N.
Can someone please help me figure out why I'm getting WA test case 6 on problem F? I am using Li-Chao Tree.
90353161
Thanks!
in the problem Permutation Cycle
why is it sufficient to break into cycles of lengths $$$A$$$ and $$$B$$$ ?
i mean — how can we be sure that the only way is when $$$A*X+B*Y=N$$$ ? why cant there be other overlapping solutions?
is this because its a functional graph? [directed graph in which all vertices have outdegree equal to 1]
Sorry for the necropost but considering the sheer number of solutions given for E, rather surprised that no one commented this.
The problem E can be solved in $$$O(K \log K \log N)$$$ time, the sum is just $$$k! [x^k] (1 + e^x)^n$$$.
This also gives us back the method used in the editorial since $$$k^n$$$ is just $$$D^k (1 + e^x)^k$$$ evaluated at $$$0$$$, and $$$D$$$ behaves exactly as $$$xD$$$ does if you replace all $$$x$$$ with $$$e^x$$$. (Here $$$D$$$ is the differentiation operator.)
Finally, here's an combinatorial species/symbolic method/intuitive explanation for the EGF. Note that the sum counts,
Let the set be $$$W_k$$$ for convenience. We define the size of the object $$$(t, S)$$$ to be the number of elements in the tuple $$$t$$$. So the size of every element in $$$W_k$$$ is $$$k$$$.
Now look at the options each element $$$i \in [n]$$$ has, either $$$i \notin S$$$ or, $$$i \in S$$$ and it appears $$$j \ge 0$$$ times in $$$t$$$.
For an element $$$i$$$, we define the object $$$j_i$$$ of size $$$j$$$ to mean $$$i \in S$$$ and it appears $$$j$$$ times in $$$t$$$, and $$$\varepsilon_i$$$ of size $$$0$$$ to mean that $$$i \notin S$$$.
So,
where $$$\star$$$ refers to the labelled product.
Now, the EGF of $$${\varepsilon, 0, 1, \dots}$$$ is simply $$$1 + \exp(x)$$$, and we are done.