Hint: When does some vowel stay in string?
Iterate over the string, output only consonants and vowels which don't have a vowel before them.
Hint 1: It's never profitable to go back. No prizes left where you have already gone.
Hint 2: The optimal collecting order will be: some prefix of prizes to you and the other prizes to your friend (some suffix).
You can find the total time with the knowledge of the prefix length. The final formula is 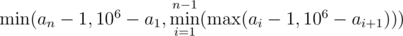 .
.
Hint: At first we will solve the problem mentioned in the statement. The formula is 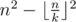 . Firstly, each submatrix k × k should have at least one row with zero in it. Exactly
. Firstly, each submatrix k × k should have at least one row with zero in it. Exactly 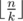 non-intersecting submatrices fit in matrix n × k. The same with the columns. So you should have at least this amount squared zeros.
non-intersecting submatrices fit in matrix n × k. The same with the columns. So you should have at least this amount squared zeros.
Now that you know the formula, you can iterate over n and find the correct value. The lowest non-zero value you can get for some n is having k = 2. So you can estimate n as about 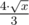 .
.
Now let's get k for some fixed n. 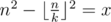

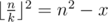

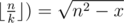

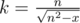 . Due to rounding down, it's enough to check only this value of k.
. Due to rounding down, it's enough to check only this value of k.
The function of the path length is not that different from the usual one. You can multiply edge weights by two and run Dijkstra in the following manner. Set disti = ai for all 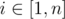 and push these values to heap. When finished, disti will be equal to the shortest path.
and push these values to heap. When finished, disti will be equal to the shortest path.
Hint 1: Count the number of times each number appears in the sum of all fa.
Hint 2: Try to find a sufficient and necessary condition that ai appears in fa of a permutation.
Hint 3: Prove that ai appears if and only if all elements appearing before it are strictly less than it (other than the largest element). And then try to solve the problem first in O(n2).
Now try to solve to simplify your solution with O(n2).
It is easy to see that i-th element appears in fa if and only if all elements appearing before it in the array are less than it, so if we define li as the number of elements less than ai the answer will be equal to:
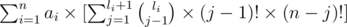
By determining the index of ai, if it is on the index j then we have to choose j - 1 of the li elements smaller than it and then permuting them and then permuting the other elements. We can find all li with complexity of O(n log n). If we were to implement this, the complexity would equal to O(n2).
Now let's make our formula better. So let's open it like so:
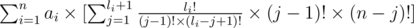
and then it equals to:
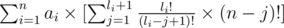
and now let's take out the li! ,
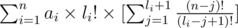
now let's multiply the inside the first sigma by 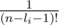 and the second sigma by (n - li - 1)! and it gets equal to:
and the second sigma by (n - li - 1)! and it gets equal to:
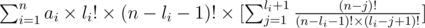
and it is easy to see it equals to:
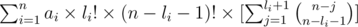
and using the fact that
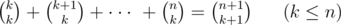
it will equal to:
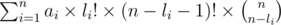
So the final answer will equal to:
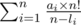
of which can be easily implemented in O(n log n). Make sure to not add the answer for maximum number in the sequence.
There is also another solution that you can read here.
Let's denote n = |s|.
Hint: There is a simple  solution: dp[m][mask] — best answer if we considered first m characters of the string and a mask of erased substrings. However, storing a string as a result of each state won't fit neither into time limit nor into memory limit. Can we make it faster?
solution: dp[m][mask] — best answer if we considered first m characters of the string and a mask of erased substrings. However, storing a string as a result of each state won't fit neither into time limit nor into memory limit. Can we make it faster?
Let's try to apply some greedy observations. Since each state represents a possible prefix of the resulting string, then among two states dp[m1][mask1] and dp[m2][mask2] such that the lenghts of corresponding prefixes are equal, but the best answers for states are not equal, we don't have to consider the state with lexicographically greater answer. So actually for every length of prefix there exists only one best prefix we will get, and we may store a boolean in each state instead of a string. The boolean will denote if it is possible to get to corresponding state with minimum possible prefix.
To calculate this, we iterate on the lengths of prefixes of the resulting string. When we fix the length of prefix, we firstly consider dynamic programming transitions that denote deleting a substring (since they don't add any character). Then among all states dp[m][mask] that allow us to reach some fixed length of prefix and have dp[m][mask] = true we pick the best character we can use to proceed to next prefix (and for a fixed state that's actually (m + 1)-th character of the string).
This is  , but in fact it's pretty fast.
, but in fact it's pretty fast.
This is a more complex version of problem G from Educational Round 27. You can find its editorial here.
To solve the problem we consider now, you have to use a technique known as dynamic connectivity. Let's build a segment tree over queries: each vertex of the segment tree will contain a list of all edges existing in the graph on the corresponding segment of queries. If some edge exists from query l to query r, then it's like an addition operation on segment [l, r] in segment tree (but instead of addition, we insert this edge into the list of edges on a segment, and we make no pushes). Then if we write some data structure that will allow to add an edge and rollback operations we applied to the structure, then we will be able to solve the problem by DFS on segment tree: when we enter a vertex, we add all edges in the list of this vertex; when we are in a leaf, we calculate the required answer for the corresponding moment of time; and when we leave a vertex, we rollback all changes we made there.
What data structure do we need? Firstly, we will have to use DSU maintaining the distance to the leader (to maintain the length of some path between two vertices). Don't use path compression, this won't work well since we have to do rollbacks.
Secondly, we have to maintain the base of all cycles in the graph (since the graph is always connected, it doesn't matter that some cycles may be unreachable: by the time we get to leaves of the segment tree, these cycles will become reachable, so there's no need to store a separate base for each component). A convenient way to store the base is to make an array of 30 elements, initially filled with zeroes (we denote this array as a). i-th element of the array will denote some number in a base such that i-th bit is largest in the number. Adding some number x to this base is really easy: we iterate on bits from 29-th to 0-th, and if some bit j is equal to 1 in x, and a[j] ≠ 0, then we just set 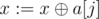 (let's call this process reduction, we will need it later). If we get 0 after doing these operations, then the number we tried to add won't affect the base, and we don't need to do anything; otherwise, let k be the highmost bit equal to 1 in x, and then we set a[k]: = x.
(let's call this process reduction, we will need it later). If we get 0 after doing these operations, then the number we tried to add won't affect the base, and we don't need to do anything; otherwise, let k be the highmost bit equal to 1 in x, and then we set a[k]: = x.
This method of handling the base of cycles also allows us to answer queries of type 3 easily: firstly, we pick the length of some path from DSU (let it be p), and secondly, we just apply reduction to p, and this will be our answer.










@BledDest Sir , in problem C , why are we taking only non-intersecting submatrices of size k x k? Here's what my thought process was for the problem C : let's suppose we have a matrix of size n x n and let us consider a submatrix of size k x k. Now to ensure there are minimum number of zeros(i.e max no of 1s), we'll place 0 at rightmost bottom most cell of the k x k matrix and now we'll consider the total number of submatrices of size k x k sharing this 0, and that would be according to me k x k number of submatices. Now if we consider total number of submatrices(intersecting and non intersecting) of size k x k in the matrix of size n x n , then that would (n-k+1) x (n-k+1) , so according to my deductions , the formula should be (n^2 — ((n-k+1)^2)/(k^2)) which is wrong as per the editorial? Could you help me with what am I thinking wrong? Sorry to bother you , if my question is stupid..
The main problem is that you can't always put zeroes in such a way that k × k submatrices are covered by this zero.
For example, let n = 4, k = 2:
According to your algorithm we put the first zero in cell (2, 2) and cover 4 submatrices:
And now it's impossible to put a second zero to cover 4 submatrices we didn't cover previously.
i was doing a silly thing!!, ignore.
This obviously doesn't give us maximum possible number of ones, since for n = 5 and m = 3 we can use the following:
And for n = 5 and m = 2 — the following:
oh yes! thank you for resolving my doubt
@BledDest
if we do:
1111
1010
1111
1010
we have covered all submatrices. now say t=15 , we get perfect square x(>=15) x=16 ,so given 1s =15 hence 0s are 1(16-1) now answer could be 4 3
1111
1111
1101
1111
if t=12 then zeroes can be:16-12=4 so answer is 4 2
1111
1010
1111
1010
and for all t from 16 to 21 answer:-1 isn't that approach right?
Yes, from every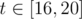 answer is - 1 since if we set n = 4, then we can't obtain anything greater than x = 15; and if we set n ≥ 5, then x ≥ 21 (if we don't consider m = 1).
answer is - 1 since if we set n = 4, then we can't obtain anything greater than x = 15; and if we set n ≥ 5, then x ≥ 21 (if we don't consider m = 1).
but I did it that way,and get WA
I don't know why my D passed. I just ran DFS multiple times (10 times DFS passed) and in each time I took the minimum of that node and all it's neighbors. Is this logic correct or just my luck that it passed. Thanks.
Why do you only use 25 for used?
It passed with 10 only. I still don't know how it works. I thought 2 DFS might be sufficient but it wasn't the case. If I increase the number of times I do DFS it will time out.
I wrote n^2 solution for E, but it got WA#16 instead of expected TLE
Can somebody help me?
cnt2[i]+=(fact[i-1]*fact[n-j-1])%MD/fact[i-1-j];You can't do this. If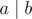 , it doesn't mean that
, it doesn't mean that 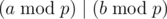 . In fact, you should use the modulo inverse instead of division. (i.e. use a × b - 1 instead of
. In fact, you should use the modulo inverse instead of division. (i.e. use a × b - 1 instead of  .) You can use Fermat's little theorm (i.e.
.) You can use Fermat's little theorm (i.e. 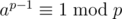 when p is a prime and (a, p) = 1) and quick pow to work out
when p is a prime and (a, p) = 1) and quick pow to work out 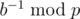 when p is a prime. Otherwise, you can use extended euclidean algorithm instead. Hope this will help.
when p is a prime. Otherwise, you can use extended euclidean algorithm instead. Hope this will help.
Hi, thank you so much for your answer. I did what you said but now i have WA#5. Any suggestions?
Edit: Fixed Thank you again :)
Final solution
I was trying to solve D using a DFS and updating a DP array for each node. Can someone point out what is wrong with my logic?
http://codeforces.net/contest/938/submission/35438377
You should read about the Dijkstra algorithm. I'll try explain the difference with your solution briefly. Doing right way we should take a node with the smallest distance to it and then update the information for its neighbours. After that we should delete this node from our list ( Dijkstra proved it ) and then repeat the first step until we considered all the nodes of the graph. This update in your solution can be wrong very often:
Value in dp[v] is not correct. Example:
Your solution is good without "visited", but then it will be O(n^3).
I guess I'm late to the party, but when I implement this Dijkstra without keeping a count of visited cities I get Time-out, but the solution gets Accepted as soon as I ignore the cities which I have already visited. Also, for some questions like this: 20C Dijkstra, I don't need any visited array to pass the tests.
Could you please explain why does this happen. Obviously, analyzing the Time-complexity is the key, but I find it hard to visualize what's happening. Thanks in advance.
Well, it was a long time ago, so I can't tell a lot. First of all, the main idea of Dijkstra is to keep array of visited cities. Otherwise, you would iterate over cities you've already visited again and again, that's why you get timeout. It's just an infinite loop. What about visualization you can look at wiki page. There is a good gif out there that explains a lot — https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
Good luck with competitive programming :)
could any one tell me what's the upper bound of n and why it is in problem C? well i mean while iteration.
I've solve it. The range of n should be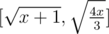 when x ≠ 0 .
when x ≠ 0 .
huangwenlong, can you explain how did you get the upper bound?
Sorry for the late reply. We can get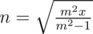 , from
, from 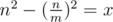 . If x ≠ 0, m should not be less than 2. So when m = 2,
. If x ≠ 0, m should not be less than 2. So when m = 2, 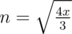 . When m = n,
. When m = n, 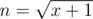 . And we can conclude that
. And we can conclude that 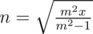 is a decreasing function. So the range is
is a decreasing function. So the range is 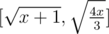 .
.
In E problem,
for every 2 ≤ i ≤ n if aM < ai then we set fa = fa + aM and then set M = i.
Does this statement mean,
or
Please, somebody help.
First code without "else break" is correct.
thank you. :)
Hi everybody.
Here is my code which uses FFT (Fast Fourier Transform) to solve Task E. It doesn't fit in time and memory limits (works well for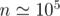 ) but it's good for educational purposes. Actually it has
) but it's good for educational purposes. Actually it has 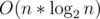 time complexity but FFT has a large constant so it takes around 10secs for
time complexity but FFT has a large constant so it takes around 10secs for 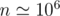 .
.
I don't understand how can we use Dijkstra to actually find closest j for every i. Why does solution in editorial works? Can someone explain?
same question here
consider a new node(v) in addition to all given vertices.This node represents watching a concert. properties: has n edges with weight equal to costs of watching a concert for each vertex. now the problem reduces to single source shortest path between v and all remaining vertices(people from all cities have to (watch a concert so reach node v )in minimum cost) which is solved by dijkstra's.
Thanks bro!!
Consider a vertex having Min(a) (All of them in case of having multiple minimums) and name it "u". The answer for this (those) city is ai. Lest consider the next minimum (Min2(a)) and name it "v". There are two cases. it can go to the city having Min1(a) or just stay there(why?). This property holds for every vertex having Mini(a). It can go to one of those vertexes having Minj(a) with j ≤ i.
Now we assume that it's better for vertex "v" to go to vertex "u". on the shortest path from "v" to "u" there is a vertex (call it "x". Of course it can be "v" itself) which is adjacent to "u". It can be easily proved that best answer for vertex "x" would be to go to "u".
So what it means? every time we find the answer for some vertex we can relax all of its neighbors and then we are done with remaining vertex having minimum found answer.
For problem C: I searched for two divisors of x with same parity and found n & n/k .then re-checked.Can someone explain what is wrong with the code? http://codeforces.net/contest/938/submission/35461430
In C problem
how we concluded that if: floor(n/k)=sqrt(n^2 -x)
then k=n/sqrt(n^2-x) ???
@BledDest Sir, one small doubt, I can't get my head around this problem C,
so suppose x = 14, then can't my answer be n = 4 and m = 4 because if my m = 4 then my whole matrix has zeroes > 0.
Like this:- 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0
Here i am considering m = 4 that is whole matrix ?
I know many people asked doubts related to problem C but I am still not able to understand this flow ? I know my question is stupid but please help me this last time.
Your answer for x = 14 can't be n = 4 and m = 4, because if n = 4 and m = 4, the maximum number of ones is 15:
BledDest Can you please explain a bit more on time complexity of dynamic connectivity?
As per the approach of editorial , if we have to add an edge to an interval
(L,R)then we will just insert it into segment tree nodes which lie completely under this range(but we will not push it further down).Doubt : Since there can be atmost
log(n)nodes containing that range and if we are doing union by size/rank than it will takelog(n).Time complexity should be :
nlog(n)log(n)log(c)...since each edge can occur in dfs atmost log(n) times and log(n) for their union operation and log(c) for gaussian elimination part first comment in this blog explains it .PS: please correct me if i am interpreting it in wrong way.
You don't have to multiply the logarithm that comes from Gauss and the logarithm that goes from DSU. The union operation is used only in DSU (so it's ), and if it is unsuccessful, then we perform only one operation with Gaussian elimination. So the complexity is
), and if it is unsuccessful, then we perform only one operation with Gaussian elimination. So the complexity is 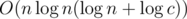 .
.
Sorry my analysis was wrong ,we will first do
log(n)to check for their parents and if they are different then we will union them and if they are same we will dolog(c)(new cycle) for gaussian elimination...so basicallylog(c)+log(n)for each edge during dfs.thank you so much it is clear now.
Could someone explain more about the simple O(n3logn) dp solution of problem F mentioned in the tutorial?
dp[m][mask] has an O(n^2) number of states, and in every state we traverse O(logn) position to decide which we use, and we use string compare to judge which we choose so there is another O(n)
ps:"abcd--> abd --> a" is equal to "abcd --> acd --> a". So we can choose 2^i in turn.
Far better than awoo's editorial. Kudos!
A direct explanation for Problem.F. Let's denote dp[i][j] as the i-th character of the minimum substring after we remove (j-i) characters from S[1...j].
Let i iterate from 1 to the length of result, and let j iterate from 1 to n.For dp[i][j], there are two possibilities:
1.We will get the minimum substring without removing S[j], it is equivalent to such a fact that there is a number m which is 0 or a single bit of(j-i) satisfies dp[i-1][j-m-1]=min(dp[i-1][i-1],dp[i-1][i],dp[i-1][i+1],...,dp[i-1][n]).In this way dp[i][j]=S[j].
2.If we have to remove S[j] to get the minimum substring, it produces following dp transition : dp[i][j]=min(dp[i][j-m1], dp[i][j-m2],...,dp[i][j-mt]), m1,m2,...,mt is the single bit of (j-i).
I believe that the first solution could be optimized to $$$O(n^2\log^2{n})$$$ since for each state in $$$dp[m][mask]$$$ we need to store only positions of $$$O(\log n)$$$ segments.
My Approch and solution for problem C.
Link