Hello, Codeforces!
We're going to host a new contest at csacademy.com. Round #72 will take place on Wednesday, 07/March/2017 15:05 (UTC). This contest will be a Div1 + Div2, with 7 tasks of varying difficulty that need to be solved in 2 hours.
We are glad to have ko_osaga as a problem setter.
Facebook event
Recently, Facebook has reintroduced the possibility of recurring events. If you choose "Interested" here, you will be notified before each round we organise from now on.
Contest format:
- You will have to solve 7 tasks in 2 hours.
- There will be full feedback throughout the entire contest.
- Tasks will not have partial scoring, so you need to pass all test cases for a solution to count (ACM-ICPC-style).
- Tasks will have dynamic scores. According to the number of users that solve a problem the score will vary between 100 and 1000.
- Besides the score, each user will also get a penalty that is going to be used as a tie breaker.
Prizes
We're going to award the following prizes:
- First place: 100$
- Second place: 50$
About the penalty system:
- Computed using the following formula: the minute of the last accepted solution + the penalty for each solved task. The penalty for a solved task is equal to log2 (no_of_submissions) * 5.
- Solutions that don't compile or don't pass the example test cases are ignored.
- Once you solve a task you can still resubmit. All the following solutions will be ignored for both the score and the penalty.
If you find any bugs please email us at [email protected]
Don't forget to like us on Facebook, VK and follow us on Twitter.











Since the customary comment from wefgef is missing.
bump! : Starts in around 30 minutes.
Hope you enjoyed the contest! I'm sorry for difficulty distribution :/
Let's denote Ls and Ld as the given starting node and destination node.
Distance is obviously 0 if Ls is Le, and 1 if Ls and Le don't have common sections. Distance is 2 if there exists an interval k such that the union of Ls and Le and k don't have common section.
Now let's analyze other cases. We can assume that Ls and Le intersects, and either Ls doesn't contain Le, or Le doesn't contain Ls (otherwise, we don't have a path from Ls to Le).
We have two interesting sets of interval : One set SL is left to the common section of Ls and Le, and the other set SR is right to the common section of Ls and Le. WLOG assume Ls have lower endpoint (and startpoint) then Le.
Now, if SL is empty, then Le doesn't have any adjacent node, so answer is -1. Similarly, if SR is empty, then Ls doesn't have any adjacent node, so answer is -1 too. If we assume both sets are nonempty, then any node in SL is adjacent to SR. So we have distance 3.
With all those observations, we have to identify whether there exists an interval that is left/right to given interval. This boils down to finding an interval with maximum or minimum starting / ending points, which can be done by priority queues.
Also, if you followed those proofs, you can notice that only intervals with minimum endpoints and maximum startpoints are relevant — so you can just look at 4 intervals (by maintaining such intervals with priority queues) and run any shortest path algorithms, like BFS or Floyd-Warshall.
The total time complexity is O(QlgQ).
If we have a magic comparator that compares two intervals enough fast, then this is a simple sorting problem with time complexity O(MlgM * ComparatorTime). Can you find such a comparator?
As the weights are exponentially increasing, we can see the maximum matters in most cases, and this is indeed true if two interval are disjoint, because the sum is bounded to [2Max, 2Max + 1 - 1]. However, intervals are not disjoint in this case!
We can extend above solution to support query operations for two overlapping intervals. If one interval contains others, then the answer is obvious. So we can assume that two interval A, B are not disjoint, and one does not contain another.
Now, we can make both intervals to be disjoint, by removing their intersections. Now,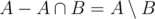 and
and 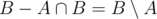 are both nonempty and disjoint intervals, and their comparison results are obviously same as comparison of A and B, So we can simply compare their maximum.
are both nonempty and disjoint intervals, and their comparison results are obviously same as comparison of A and B, So we can simply compare their maximum.
With well known RMQ structures such as tournament tree, we can use only O(lgN) operations for interval maximum, which results in O(MlgMlgN) algorithm that is fast enough to solve this problem. With "sparse table", you can use only O(1) operations, which makes the solution even faster — O((N + M)lgN).
One natural strategy is to adapt some existing MST algorithms, and exploit the nature of problem to reduce it's time complexity. There are a lot of well known MST algorithms, such as Jarniks-Prim, or Kruskal. However, both have a serious problem — the problem makes it really hard to retrieve single edge weights. What is the workaround?
While less famous than Jarnik and Kruskal's, there is also an algorithm called Borůvka's Algorithm — the first known algorithm for Minimum Spanning Tree. In Boruvka's algorithm, all we have to do is finding a smallest outgoing edge for each component. As some kind of batch processing is allowed now, it sounds that sweep line can help. Can you see how?
In Borůvka's algorithm, we find a smallest edge leading to other components for each component, and add it to spanning tree. We will instead find a smallest outgoing edge for each node (with different component labels), which we can easily merge for a component.
We will find the smallest outgoing node from 1 to n, in order. As rectangles are events adding constant values in the interval, we can use sweep line approach — the cost of edge outgoing from node i can be maintained in a simple array with O(N) operations per query.
Now, we have to find a node with minimum edge weight, with different component origin, which can be also done in O(N) operations per nodes. Note that Borůvka's algorithm needs careful attention for edges with same costs — If there are ties, picking the one with smallest node number is a good tie-breaking rule. This leads to an O((Q + N)NlgN) time complexity, and O(N) space. It's still too slow, but it's the first algorithm with feasible space complexity.
The bottleneck is in finding minimums, and adding constant value in an interval — which hints toward a segment tree approach. If we were to find a minimum edge weight, without different component restriction, then the problem is a classical lazy propagation — we will omit the details.
To support finding minimum value with different component origin, we can slightly modify the segment tree. For each node, we record two minimums — first one gives minimum value, and second one gives minimum value among the node that have different component than first. This modification still allows lazy propagation and query exactly same as before, so we can do the whole query in O(lgN) time — the complexity is O((Q + N)lg2N). The asymptotics is not huge, but due to the high constant factor of segment tree, the solution doesn't run that fast — that's why we have a huge time limit.
Thanks to Konijntje for providing problem F (Diamond Dogs)!
Thanks for the fast editorials!
What's the difference between a tournament tree and a standard max segment tree? Does anyone have resources for learning about this?
tournament tree is often referred as "bottom-up segment tree". Maybe you might know what it is.
Something like this?
Yup
Yeah, tournament tree is nothing new but a standard max segtree. There's a ton of way to call such binary tree, for example "indexed tree", "non-recursive segment tree", "bottom-up segment tree", "RMQ", "max segtree", etc..
However, recently I started to use the word "tournament tree". This word expresses the nature of the DS very well, and it's also short and clear.
Do you use tournament tree in this case because iteration is faster than recursion or is there more?
Just because why not..? Tournament trees are easier to implement
I used segment tree and i got TL; but then i random shuffled dogs before sorting and it passed!
I just got an AC with normal segment tree with no randomization. Here, is the link to my submission https://csacademy.com/submission/1420487/
ko_osaga Please take a look at this for problem circle kingdom.
https://csacademy.com/submission/1421015 (Acc solution after contest)
https://csacademy.com/submission/1412943 (TLE during contest)
Both have same code with just Input difference. I suppose scanf is fast enough but it times out. Why ?
https://csacademy.com/submission/1413899/
https://csacademy.com/submission/1413832/
I also had the same issue, but with the memory problem , one leads to TLE(with lower memory)and other one to AC(with higher memory usage).
This dynamic scoring is a piece of crap. It should be turned off. Not only it does not work: in div 2 contests, div 1 participants affect dynamic scoring. But also it provides strange point values, i.e. 300 points for C and D even though one was solved by 49% and the other by 34% and 100 pts for A which was solved by 96%...
It seems that your arguments are against the way the dynamic scoring is implemented, not against dynamic scoring itself.
Would you prefer a wider range of score distribution? (so that C and D would have diferent scores)
Also using Div1 contestants to change the dynamic score in Div2 contests is arguably better because it is a larger sample of people to define better the score
You may disagree, but I dont see why any of this is such a big deal
Talking about the pretest system in codeforces though...
Approach for beautiful matrix?
Border row/column contributes A[1] + 2*(A[2]+A[3]+..+A[N-1]) + A[N], whilst middle 2 times more. Calculate such sum for every row/column and consider exchanging border ones with 3 smallest middle ones. Chose the best swap.
Well my approach was same but I replaced border row/column with only 1 smallest row/column. Can you explain how you arrived at the conclusion of replacing with 3 smallest row/column. Thanks.
Even trying to replace with every other row will fit time limit. Now, when I'm thinking about it, it looks like 2 is enough.
You may have the following case:
first row is smallest
last row is second smallest
I was thinking that you may not be able to replace the first 2 smallest values, but... it is already an optimal case. No need to replace anything. You must check 2 in case the smallest is already placed on the border.
Edit. When I looked again on my previous answer — 1 smallest middle value is definitely enough. But as I already mentioned, in order to get that, you should check 3 globally smallest values. And as I wrote above looks like just 2 of them will be fine.