242A - Игра в монетку
Эта задача решалась очень просто: достаточно было двумя вложенными циклами по i и по j (a ≤ i ≤ x, b ≤ j ≤ y) перебрать всевозможные исходы игры и выделить среди них те, в которых i > j. Такие пары и составляют ответ. Время – O(x·y).
242B - Большой отрезок
Для начала заметим, что ответ всегда однозначный, потому что если существует отрезок номер i, который покрывает отрезок номер j, то отрезок j никак не может покрывать отрезок i. Единственный случай, когда такое возможно, — это когда отрезки i и j совпадают, однако по условию в наборе нет одинаковых отрезков. Заметим, что ответ должен покрывать самую левую из всех точек всех отрезков, и аналогично, самую правую из всех точек. Таким образом, надо найти эти точки линейным проходом: L = min(li), R = max(ri), и найти номер отрезка [L, R], либо вывести - 1, если его нет в заданном множестве. Время --– O(n).
242C - Путь короля
Самое главное для решения этой задачи – заметить, что суммарная длина всех отрезков не превосходит 105. Используя этой свойство, мы можем занумеровать все разрешенные клеточки, и найти кратчайший путь с помощью обхода в ширину. Проще всего занумеровать клеточки используя ассоциативный массив (например, map в C++). Время –-- O(n·log(n)).
242D - Спор
Обозначим через bi текущее число на счетчике номер i. Решать задачу будем следующим образом: возьмем любой счетчик i, такой, что bi = ai, и нажмем на соответствующую кнопку. Алгоритм прекратим тогда, когда такого i не найдется. Поймем, что этот алгоритм на самом деле решает задачу. Нам необходимо объяснить несколько условий:
Почему после конца алгоритма состояние будет выигрышным для Валеры? Потому что не будет существовать такого i, в котором bi = ai, а иначе мы бы нажали на кнопку.
Почему алгоритм не будет нажимать одну и ту же кнопку дважды? Потому что мы нажимаем кнопку i, только если bi = ai, и сразу же, как мы нажмем, число bi увеличится, и равенство больше никогда не выполнится.
Почему этот алгоритм можно реализовать за приемлемое время? Потому что из условия 2 следует, что алгоритм сделает не более n нажатий, которые суммарно приведут не более чем к n + 2·m прибавлениям к числам. Для того, чтобы быстро находить те числа, в которых bi = ai, можно воспользоваться очередью: каждый раз, когда мы изменили число bi, и оно стало равным ai, то закидывать в очередь i. Несложно понять, что одно и то же число не может быть закинуто в очередь дважды.
Из алгоритма следует, что ответ всегда существует, а значить выводить - 1 никогда не нужно было. Время – O(n + m).
242E - XOR на отрезке
Запишем числа a1, a2, ..., an в виде таблицы n × 20 где bi, j равно j-ому биту в i-ом числе. Тогда сумма на отрезке [l, r] равно 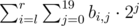 что равно
что равно 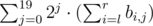 , то есть мы можем перебрать номер бита j, найти в скольких числах этот бит равен 1, и прибавить к ответу (количество)·2j.
, то есть мы можем перебрать номер бита j, найти в скольких числах этот бит равен 1, и прибавить к ответу (количество)·2j.
Для эффективной реализации воспользуемся 20-ю деревьями отрезков по сумме, каждый из которых будет соответствовать одному из битов (то есть одному из столбцов таблицы bi, j). Тогда операции можно переформулировать:
подсчет суммы эквивалентен нахождению количества единиц с l по r.
операция "xor" эквивалентна изменению всех бит c l по r на противоположные (то есть 0 меняется на 1, а 1 – на 0).
Первая операция выполняется для всех номеров бит, вторая – только для тех номеров бит, в которых у числа из входных данных стоит 1.
Обе этих операции несложно реализуются деревом отрезков с обновлением на отрезке, где у каждой вершины стоит пометка, нужно ли переворачивать все биты в поддереве.
Время — O(m·log(n)·20).











Спасибо за контест и за разбор. Задачи не очень сложные в плане алгоритмов, но действительно стоит подумать над их решением.
Если изменить 2 слова в D-шке, то она превращается в халяву) Мой погнавший мозг эти 2 слова изменил, и час пытался понять, почему прога не работает не сэмплах :D. Когда дошло, я чуть клаву не разбил
весь контест решал задачу Д, предполагая, что не должно быть вершины, на которой написано хотя бы одно ai, еще и думаю, как ее сдают серые — задача же непростая
Тогда вряд ли бы в тестах Ai повторялись. У самого сложилось такое же представление о задаче. Но тесты всё поставили на место.
Excuse me ~ Can you write a solution in English ?~^。^ I'm very impressed with your E problem and want to learn it for a lot.But I can not read Russian. So ……~~
goto this link:
http://codeforces.net/blog/entry/5837
Thanks a lot ~ ^_^
In problem E complexity should be O(n) + O(m*log(n)*20) = O(n + m*log(n)). Isn't it?
No, that is not how you calculate the sum of terms in Big-O-Notation. The correct way in this case is to take the fastest growing term, which is O(m*log(n)*20). You can read more about the Big-O-Notation for example in Wikipedia: http://en.wikipedia.org/wiki/Big_O_notation , which will tell you the following: "If a function f(n) can be written as a finite sum of other functions, then the fastest growing one determines the order of f(n)."
Why do you think that m grows faster than n in this case?
Codeforces editorials rarely give detailed explanation of the harder problems, especially when the problem is just about using an advanced data structure. The editorial just says "This can be done using interval trees.". Can someone please explain how to use segment trees in Problem E in more detail? Your explanation will be useful for all those who are just starting to learn segment trees, thanks!
check my code. 2559296
if you dont understand any of my code, please let me know.. :)
thanks for sharing your code
i understand the build function and a bit of the query and update function. can you explain what is the lazy array used for?
From looking at the code I think it is "Lazy Propagation". Search that up
I recommend that you first solve https://www.codechef.com/problems/FLIPCOIN to learn about lazy propagation with Segment tress and then solve E problem.
My solution http://codeforces.net/contest/242/submission/17871914
pro E: nx20 ??why??thanks...
because 2^20 > 1000000 so 20 bits is enough to represent every number
Really, we would really appreciate if someone could give a detailed explanation on the solution of E using segment trees. Thank you.
I think The time is O(n+m) for 242D — Dispute
I solved 242E — XOR on Segment with naive algorithm without using any data structer
look at my code it solved the problem exactly on time limit and got accepted
lol :D :D how did that code pass tests ?
4000ms!!!
Yes, one more 1ms and my code will get Time limit exeeded
This naive solution may be a little bit optimised.
Instead of using count — just check that tmp is far from overflow.
Compare solutions 3064707 and 3064734.
I_love_Tanya_Romanova, Can we solve it using fenwick tree. If no, why not ? I read some blog that we can do range update + range query using fenwick tree, but could not solve this problem using this concept. Note that I'm clear with the segtree lazy propag. solution idea.
Задачу С на Паскале сдали единицы...
Вообще не вижу, почему в С суммарная длина всех отрезков не превосходит 10^5 :( Объясните кто-нибудь, пожалуйста
Вероятно, такая особенность появляется в задаче из-за этой части условия:
Гарантируется, что начальная позиция и конечная позиция короля являются разрешенными клетками. Гарантируется, что начальная позиция не совпадает с конечной позицией короля. Гарантируется, что суммарная длина всех разрешенных отрезков не превосходит 10^5.
I solved this problem using segment tree I am getting WA on the 15 th test case can anyone help me finding bug in my code here is the link https://ideone.com/0OuZRq
I am also getting WA on test 15
can anyone please point out what is wrong with my code?here is my code http://codeforces.net/submissions/vis10326#
Clean your code first. Put some spaces and indentations would be enough
http://codeforces.net/contest/242/submission/9527768 and http://codeforces.net/contest/242/submission/2563497
The same code...i m not as lucky as the latter.
I am getting wrong answer on test 10 in problem C My code: http://codeforces.net/contest/242/submission/14186492 anyone please help
Same problem, In fact I am also getting the same answer as yours for test case 10 :/
Извините за некропостинг, но в 2018 году после того, как codeforces переехал в ИТМО, задача E сдается наивным решением за O(n*m) за 1346 ms code даже с модификатором *2 для старых задач. Мое решение деревом отрезков за O(nlog(n)*20) зашло с 1246 ms code. Эффективность дерева отрезков под вопросом?
I don't understand why we need to built separate tree for every bit . I think xor follow commutative property so i written This[ but not working ] , please correct me.
Get it :).
E : good problem
So much week testcases of problem E. Many of accepted solutions have more than 10^5 * 10^5 complexity.
lazy segment tree solution of E Xor On Segmentcode
Can anybody explain E ? Thanks.
If you are still curious about this problem — the idea is as follows. Maintain a segment tree for each bit and a lazy tree for each bit (containing info on whether ith bit is set in each of the numbers). For each update query, flip the bits in the current range and invert the child's lazy bit values, but only if the ith bit is set in the number that we xor our range with, otherwise skip to the next one. The same is applied in the sum query.
It is the standard lazy segment tree implementation with a little twist (multiple trees). Here's a link to a tutorial and my submission for further clarification:
https://codeforces.net/contest/242/submission/103977271
https://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/
can't we solve problem E with lazy-segment tree? thank you in advance..
Yes all we have to do is to construct 20 lazy segment tree for every bit.
my solution: 216845895