back_slash's blog

Chef And Interval Painting March Long CodeChef
By back_slash, history, 7 years ago, In English

Hello Everyone, Chef And Interval Painting was one of the most interesting problem of March Long. I am writing this blog for 2 main reasons listed below.

  1. I am having a hard time in understanding the editorial. And the interesting thing is I haven't even reached to the harder part of the editorial yet i.e. the NTT part. I can't understand the DP relation that they have written in the first statement. How can we say that the number of ways for exactly r colors to be visible at the end won't depend on the choice of colors which are visible? According to me because we are coloring in a specific order which can't be changed, I think it should depend on the choice of colors. It would be great if someone can provide a better approach to arrive at the solution or if someone has a different DP relation that can be used to solve the problem.

  2. The second reason is during the contest I was able to figure out a DP relation which can be used to solve the problem in O(N^2) time. But obviously, I was not able to convert that approach to a better complexity. So, I wanted to share my approach and if anyone can provide a suggestion on is it possible to apply NTT to my approach or not.

So basically, the approach which I used was dp[N][K] will denote the number of distinct coloring of an array of size N after K rounds and the only twist is coloring a subarray of size 0 is also a valid round.

So, the relation would be fairly simple

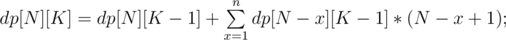
The basic logic used is same that start from reverse and coloring a subarray of any size in some round X won't affect the coloring in the previous i.e. (X-1)th round. And the final answer for some value of N,K will be

Ans[N][K] = dp[N][K] - dp[N][K - 1];

I don't know if the above relation can be solved in less time complexity or not. But any suggestion related to the problem are welcomed.

Thanks !!

  • Vote: I like it
  • +11
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +19 Vote: I do not like it

I have managed to find the recursive relation: ans[n,k]=ans[n,k-1]+ans[n-1,k]+(n-1)*ans[n-1,k-1]

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I also

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    What you have is perfectly correct. It shouldn't be difficult to transform your equation to the one back_slash has in the post and vice versa.

    Consider a different version of the problem; if you know for sure that all K colors will show up in the final array, there is no need for your ans[n][k — 1] term (since this term comes from the fact that you can choose to not use the Kth color).

    You can easily convert this version to the actual problem by choosing which colors will be visible in the final array. You know the Kth color will definitely show up, therefore, if R colors end up visible in the final array, you have a choice of

    C(K - 1, R)

    So the answer would be more or less similar to,

    Now all we have to do is to calculate

    dp[n][i]

    which now has the recursive relation

    dp[i][j] = dp[i - 1][j] + (i - 1) * dp[i - 1][j - 1]

    Look up Stirling numbers of the first kind. They have the same recursive relation, and they can be calculated using coefficients of the polynomial mentioned in the editorial.

    → Reply