Once again you are invited to participate in the online mirror of the final stage of Lithuanian Olympiad in Informatics!
The format of the competition is similar to IOI: 2 days with 3 tasks in 5 hours, just the choice of languages is more limited (programming: C/C++, statements: English/Lithuanian). Day 1 contest will start on Friday, March 23 at 15:00 UTC and day 2 on Saturday, March 24 at 9:00 UTC.
See online.lmio.lt for more information.
Update: Congratulations to the winners! See the results of online and onsite contests.
Online:
Onsite:











At the same time we have our national competition so I won't be able to participate in online mirror. Can you please leave server open for at least a few days (like analysis mode) so I can make my own "virtual competition" (problems from previous years were very interesting and I would really like to take part)?
Yes, most likely there will be analysis mode after both contests finish.
Great, thank you.
Auto comment: topic has been updated by Martynas (previous revision, new revision, compare).
Where can I find previous years' problems?
Good question. 2015 problems are here, and I'll find the other years later.
What does the 'M' in 'LMIO' stands for? And it is "Lithuanian Olympiad in Informatics", but why is the short form 'LMIO' but not 'LMOI'?
LMIO is the initialism of the Lithuanian name of the olympiad, and there M is for "mokinių", which means "pupils'" (the participants are high school students).
Here are my ideas for problem A and B —
Lets assume all bus edges have cost 1, and train edges have cost 0. Now the problems becomes — Count number of nodes from which you can reach all nodes in cost ≤ 1.
Lets shrink the graph into components and make a new graph. Nodes u and v is in same component if distance from u to v is 0. This can be done in linear time.
Let C be the number of nodes(component of actual graph) in new graph. Add size of ith component to answer if its node in new graph connected to all other nodes, in other words, degree of node i in new graph is C - 1.
It is easy to see why this works. Complexity O(n + m).
First thing to notice is that our answer is always an induced star graph or a triangle. The first case can be handled naively by just looking at adjacent nodes of each node. And for the second case you can take each edge and try to make a triangle with its end points.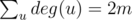 . So there are at most
. So there are at most 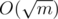 nodes with degree greater than
nodes with degree greater than 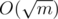 , all other nodes should have degree less than this. So, for each edge, if you iterate on the adjacency list of the node with lower degree, in total you'll take
, all other nodes should have degree less than this. So, for each edge, if you iterate on the adjacency list of the node with lower degree, in total you'll take 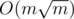 .
.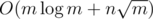
But a thing to notice is that
Since there are no self loops and multiple edges, you can prove that you always get answer if you look at O(n) edges with higher weight (think about what happens if there isn't a triangle with one side in highest O(n) edges while there is a triangle somewhere else. It leads to a contradiction).
It will result into something like
How to solve C?
There is a faster solution to B. For each vertex consider triangles that have smallest edge opposite to this vertex (otherwise that triangle will be considered from other vertex), If this triangle doesn't use two highest edges of this vertex, we'll get better answer by replacing third edge with biggest edge from this node, so for each node we only have to consider triangle formed by two biggest edges from this node.
Can you please tell me how you managed to do first part in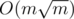 ? I got the same idea but I got an extra log2(n) factor because I used set to find element in larger set?
? I got the same idea but I got an extra log2(n) factor because I used set to find element in larger set?
I used
unordered_map<int, int> v[N]for that. Though it is not true O(1), but it passed.Thank you.
Have the servers died?
i want to ask the same.
it is working now !
The site was (and still is) lagging during the last 10 minutes (and I also had a submission that was stuck on compilation), and is now down for me (504 gateway time-out).
Does anybody know anything about it?
it is working now!
How to solve problem A and B from day 2 ?
B is easy, but A is pretty hard! C needs too many strategies...
I solved the problem by going through all the possible solutions (taking the best one of course) and using pretty simple observations:
With this, if we have 2 lines that represent 2 solutions, then the only possible way to multiply and add will correspond to their intersection (which might not have nonnegative integer coordinates, in which case there is no answer). For example if I want to get from 2 to 5 and from 4 to 9 at the same time, then I can form the lines - 2x + 5 and - 4x + 9. They intersect at (2, 1), which means I can multiply by 2 and add 1.
Here is what I did: at any call of the recursion, I maintain the last value I printed for each string as its substring inside that string. From here I have 2 cases:
With these two, I go over all possibilities to print the next substring in their strings. For every such pair I find the intersection of those lines, and if their intersection leads to some valid pair (x1, y1), then I go over all strings, apply this transformation on all their previously printed substrings and check whether the result is a prefix of the remaining string I need to print. If this is true for all strings (which is a rare case), then I can continue the recursion with these operations being applied.
With every call I also maintain the steps I performed. The cases that end the recursion are if I finished all strings (which means it's a valid answer), if I finished only some of the strings (which means it's an invalid answer).
There's also something to be aware of: if in some string, the next character I need to print is 0, then the operation that must be applied is "multiply 0".
Unfortunately, I don't know the complexity of this solution, but on all cases it wrote that I took 0.000s.
First off we sort the values in the array. Now every set of values we pick will be contiguous, because if we pick a start value and an end value then we can take any value between them and the answer won't increase.
Let's binary search on the answer, on the current iteration we're checking whether we can solve the problem with the answer being ≤ X. Let DPi be 1 if we can split the first i values to valid groups such that the answer does not exceed X.
Notice that with the current X, we can compute for each value in the array the leftmost value such that their difference does not exceed X (which means, we can find the largest segment we can take which ends on that value). We can compute this in amortized using 2 pointers. This segment will also have a lowerbound of a and an upperbound of b over its length. For an index k, we will denote the leftmost index and the rightmost index on which that segment can start at, as lk and rk respectively.
using 2 pointers. This segment will also have a lowerbound of a and an upperbound of b over its length. For an index k, we will denote the leftmost index and the rightmost index on which that segment can start at, as lk and rk respectively.
Now we have a formula for DPk: it is equal to 1 if and only if there exists such an lk ≤ m ≤ rk that DPm - 1 = 1. In order to be able to solve such queries we will maintain the prefix sum of array DP, then we can query for a range sum in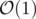 and update the current cell using the previous one. Because of the binary search, the total time complexity is
and update the current cell using the previous one. Because of the binary search, the total time complexity is 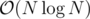 .
.
Here are my solutions for A and B, I hope they can be understood even though they're not very formally written.
There's the special case n = 1, which needs to be solved separately.
Solution for n > 1:
Let's denote length of a string s by |s| and its substring from a-th character to b-1-th character by s[a..b].
We solve the problem by using recursion. For each substring of b[0][0..i] and b[1][0..j], where 1 ≤ i ≤ |b[0]| and 1 ≤ j ≤ |b[1]|, check if it's possible to find non-negative integers x and y such that a[0]·x + y = b[0][0..i] and a[1]·x + y = b[1][0..j]. If such integers x and y exist, then check if a[k]·x + y is a substring of b[k] for every k.
If that's true for every value of k, then multiply each a[k] by x and add y to it, and erase that substring from b[k]. Keep doing this until either all b's are empty or the previously mentioned condition is false. If all strings are empty, you have found one solution, even though it's not necessarily the shortest one.
Use binary search and two pointers technique to solve the problem in .
.
Sort the given array v, and binary search for the answer k.
When checking the condition for binary search, first calculate for each i a value t[i], which is the furthest index j such that j - i < b and |v[i] - v[j]| ≤ k.
For the array v = [1, 1, 1, 5, 8, 8, 8, 10] and a = 3, b = 5 the array t would be [3, 3, 3, 6, 7, 7, 7, 7].
Now notice that if |i - t[i]| - 1 ≥ a, then you can select a subarray from i to [i + a - 1, t[i]] ie. you can "jump" from i to range [i + a, t[i] + 1]. Because array t is increasing, then both i + a and t[i] + 1 are increasing too.
We start with a queue q that contains a range $[0, 0]$, and at each i we check if there's any range [l, r] such that l ≤ i ≤ r. If there isn't any, then there's no solution for k. Otherwise we push the range [i + a, t[i] + 1] to the queue.
My 80 points solution:
Let o = [1..n].
Repeat the following process several times:
Random shuffle o. Then start doing depth first searches starting from each o[i] for every i in 0..n - 1. Every time you encounter a cycle, evacuate the node where you found this cycle. When there are no cycles you can successfully evacuate all other houses.
Because the test cases give you the number of the test case, you can try different seeds for the random number generator and find a good seed for each case.
Thanks Kuha ! I like your idea.
Will the LMIO problems be available on some judge after the analysis mode?
I'm not sure, but they'll probably be available on http://olimp.mif.vu.lt – it currently has the tasks of all other LMIO rounds from the last two years (no problem statements in English, however).
I'm just gonna download the statements from the analysis mode then.
Thanks!
Can you please send the pdfs? I have lost them :(
Also, what will be the name of that competition so I know which one to enter.
LMIO'29 (2017-2018 m.m.)
Respublikinio etapo baigiamoji dalis
Vyresniųjų grupė (10-12 kl.)
The URL will probably be http://olimp.mif.vu.lt/lmio29-4-vyr/.
Why don't ojuz upload LMIO problems?
Do they make judge data public?
Actually we didn't know the existence of this contest because there wasn't any request :( It seems tests are not provided now, I could only download 2015's one. From this comment, it seems they have their own grading system.
It seems it is possible to download the tests from the analysis mode. If we are allowed to upload those problems (since they have their own grading system) and we have English statements, we will start uploading