Разбор Educational Codeforces Round 41

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif

	int n, m;
	cin >> n >> m;
	vector<int> cnt(n);

	for (int i = 0; i < m; ++i) {
		int col;
		cin >> col;
		++cnt[col - 1];
	}
	
	cout << *min_element(cnt.begin(), cnt.end()) << endl;
	
	return 0;
}

961B - Lecture Sleep

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif

	int n, k;
	scanf("%d %d", &n, &k);
	
	vector<int> a(n);
	vector<int> t(n);
	
	int overall = 0;
	
	for (int i = 0; i < n; ++i)
		scanf("%d", &a[i]);
	for (int i = 0; i < n; ++i)
		scanf("%d", &t[i]);
		
	vector<int> pr(n);
	for (int i = 0; i < n; ++i) {
		if (i) pr[i] += pr[i - 1];
		if (t[i] == 0) pr[i] += a[i];
		else overall += a[i];
	}
	
	int add = 0;
	for (int i = k - 1; i < n; ++i)
		add = max(add, pr[i] - (i >= k ? pr[i - k] : 0));
	
	printf("%d\n", overall + add);
	
	return 0;
}

961C - Chessboard

Разбор

Решение (Ajosteen)

#include <bits/stdc++.h>

using namespace std;

const int N = 109;

int n;
string a[4][N];

int main() {
	cin >> n;
	for(int k = 0; k < 4; ++k)
		for(int i = 0; i < n; ++i){
			cin >> a[k][i];
				for(int j = 0; j < n; ++j)
			    a[k][i][j] -= '0';
		}
	
	vector <int> v;
	for(int k = 0; k < 4; ++k){
		int sum = 0;
		for(int i = 0; i < n; ++i)
			for(int j = 0; j < n; ++j)
				if((i + j) % 2 != a[k][i][j])
					++sum;
		v.push_back(sum);
	}
	
	int res = int(1e9);
	vector <int> perm;
	for(int k = 0; k < 4; ++k) perm.push_back(k);
	do{
		int sum = 0;
		for(int k = 0; k < 4; ++k){
			int id = perm[k];
			if(k & 1)
				sum += v[id];
			else
				sum += n * n - v[id];
		}
		
		res = min(res, sum);
	}while(next_permutation(perm.begin(), perm.end()));

	cout << res << endl;
}

961D - Pair Of Lines

Разбор

Решение (adedalic)

#include <bits/stdc++.h>

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)

#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair

#define x first
#define y second

using namespace std;

typedef long long li;
typedef pair<int, int> pt;

inline pt operator -(const pt &a, const pt &b) {
	return {a.x - b.x, a.y - b.y};
}

inline li cross(const pt &a, const pt &b) {
	return a.x * 1ll * b.y - a.y * 1ll * b.x;
}

const int N = 200 * 1000 + 555;

int n;
pt p[N];

inline bool read() {
	if(!(cin >> n))
		return false;
	
	fore(i, 0, n)
		scanf("%d%d", &p[i].x, &p[i].y);
	return true;
}

bool used[N];

bool check() {
	int i1 = -1, i2 = -1;
	fore(i, 0, n) {
		if(used[i])
			continue;
		if(i1 == -1)
			i1 = i;
		else if(i2 == -1)
			i2 = i;
	}
	if(i2 == -1)
		return true;
		
	fore(i, 0, n) {
		if(used[i])
			continue;
		if(cross(p[i2] - p[i1], p[i] - p[i1]) != 0)
			return false;
	}
	return true;
}

bool check2(pt a, pt b) {
	memset(used, 0, sizeof used);
	fore(i, 0, n)
		if(cross(b - a, p[i] - a) == 0)
			used[i] = 1;
	return check();
}

inline void solve() {
	if(n <= 2) {
		puts("YES");
		return;
	}
	
	if(check2(p[0], p[1]) || check2(p[0], p[2]) || check2(p[1], p[2]))
		puts("YES");
	else
		puts("NO");
}

int main(){
	if(read()) {
		solve();
	}
	return 0;
}

961E - Tufurama

Разбор

Решение (Ajosteen)

#include <bits/stdc++.h>

using namespace std;

const int N = 200 * 1000 + 9;

int n;
int a[N];
int f[N];
vector <int> v[N];

void upd(int pos, int d){
	for(; pos < N; pos |= pos + 1)
		f[pos] += d;
}

int get(int pos){
	int res = 0;
	for(; pos >= 0; pos = (pos & (pos + 1)) - 1)
		res += f[pos];
	return res;
}

int main() {
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", a + i);
		--a[i];
	}
		
	for(int i = 0; i < n; ++i){
		if(a[i] < N)
			v[a[i]].push_back(i);
		upd(i, 1);
	}
	
	long long res = 0;
	for(int i = 0; i < n; ++i){
		int to = min(N - 1, a[i]);
		res += get(to);
		for(auto x : v[i])
			upd(x, -1);
	}
	
	for(int i = 0; i < n; ++i)
	    if(i <= a[i])
	        --res;
    assert(res % 2 == 0);
    
	cout << res / 2 << endl;
}

961F - k-substrings

Разбор

Альтернативное решение (jtnydv25)

Решение (adedalic, суффиксный массив)

#include <bits/stdc++.h>

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)

#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair

#define x first
#define y second

using namespace std;

typedef pair<int, int> pt;

const int LOGN = 21;
const int N = 1000 * 1000 + 555;

int n;
string s;

inline bool read() {
	if(!(cin >> n))
		return false;
	
	char buf[N];
	assert(scanf("%s", buf) == 1);
	s = buf;
	return true;
}

pair<pt, int> d[N], curP[N];
int szd = 0;

int cnt[N], szcnt;
int rdp[N];

inline void radix_sort() {
	fore(k, 0, 2) {
		szcnt = 0;
		fore(i, 0, szd) {
			int val = k == 0 ? d[i].x.y : d[i].x.x;
			while(szcnt <= val)
				cnt[szcnt++] = 0;
			cnt[val]++;
		}
		int sum = 0;
		fore(i, 0, szcnt) {
			rdp[i] = sum;
			sum += cnt[i];
		}
		
		fore(i, 0, szd) {
			int val = k == 0 ? d[i].x.y : d[i].x.x;
			curP[rdp[val]++] = d[i];
		}
		fore(i, 0, szd)
			d[i] = curP[i];
	}
}

int c[N], id[N];
int lcp[N];

int lg[N];
int st[LOGN][N];

void precalc() {
	s += '$';
	for(int len = 1; len < 2 * sz(s); len <<= 1) {
		szd = 0;
		fore(i, 0, sz(s)) {
			int sh = len >> 1;
			d[szd++] = {len == 1 ? mp((int)s[i], 0) : mp(c[i], c[(i + sh) % sz(s)]), i};
		}
		radix_sort();
		
		c[d[0].y] = 0;
		fore(i, 1, szd)
			c[d[i].y] = c[d[i - 1].y] + (d[i - 1].x != d[i].x);
		
		if(c[d[szd - 1].y] == sz(s) - 1)
			break;
	}
	
	fore(i, 0, sz(s)) {
		c[i]--;
		if(c[i] >= 0) id[c[i]] = i;
	}
	s.pop_back();
	
	int l = 0;
	fore(i1, 0, n) {
		l = max(l - 1, 0);
		if(c[i1] == n - 1)
			continue;
		
		int i2 = id[c[i1] + 1];
		while(i1 + l < n && i2 + l < n && s[i1 + l] == s[i2 + l])
			l++;
		lcp[c[i1]] = l;
	}
	
	lg[0] = 0;
	fore(i, 1, N) {
		lg[i] = lg[i - 1];
		if((1 << (lg[i] + 1)) <= i)
			lg[i]++;
	}
	
	fore(pw, 0, LOGN) {
		if(pw == 0) {
			fore(i, 0, n)
				st[pw][i] = lcp[i];
			continue;
		}
		fore(i, 0, n) {
			st[pw][i] = st[pw - 1][i];
			if(i + (1 << (pw - 1)) < n)
				st[pw][i] = min(st[pw][i], st[pw - 1][i + (1 << (pw - 1))]);
		}
	}
}

inline int getMin(int l, int r) {
	if(l >= r) swap(l, r);
	
	int len = lg[r - l];
	return min(st[len][l], st[len][r - (1 << len)]);
}

inline bool eq(int i1, int i2, int l) {
	if(i1 == i2) return true;
	return getMin(c[i1], c[i2]) >= l;
}

int l[N], mx[N];

inline void solve() {
	precalc();
	
	fore(i, 0, n / 2) {
		int c1 = i, c2 = n - 1 - i;
		if(s[c1] != s[c2]) {
			l[i] = -1;
			continue;
		}
		int lf = 0, rg = min(c1, n - 1 - c2) + 1;
		while(rg - lf > 1) {
			int mid = (lf + rg) >> 1;
			
			if(eq(c1 - mid, c2 - mid, 2 * mid + 1))
				lf = mid;
			else
				rg = mid;
		}
		l[i] = lf;
	}
	
	fore(i, 0, n / 2) {
		if(l[i] < 0)
			continue;
		mx[i - l[i]] = max(mx[i - l[i]], 2 * l[i] + 1);
	}
	fore(i, 1, n / 2)
		mx[i] = max(mx[i], mx[i - 1] - 2);

	fore(i, 0, (n + 1) / 2) {
		if(i) printf(" ");
		printf("%d", mx[i] == 0 ? -1 : mx[i]);
	}
	puts("");
}

int main(){
	if(read()) {
		solve();
	}
	return 0;
}

Решение (adedalic, хеши)

#include <bits/stdc++.h>

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)

#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair

#define x first
#define y second

using namespace std;

typedef long long li;

const li MOD = li(1e18) + 3;
const li BASE = 1009;

inline li norm(li a) {
	while(a >= MOD)
		a -= MOD;
	while(a < 0)
		a += MOD;
	return a;
}

inline li mul(li a, li b) {
	li m = ((long double)(a) * b) / MOD;
	return norm(a * b - m * MOD);
}

const int N = 1000 * 1000 + 555;

int n;
string s;

inline bool read() {
	if(!(cin >> n))
		return false;
	
	char buf[N];
	assert(scanf("%s", buf) == 1);
	s = buf;
	return true;
}

li h[N], pw[N];

inline void precalc() {
	h[0] = 0;
	fore(i, 0, n)
		h[i + 1] = norm(mul(h[i], BASE) + s[i] - 'a' + 1);
		
	pw[0] = 1;
	fore(i, 1, N)
		pw[i] = mul(pw[i - 1], BASE);
}

inline li getHash(int l, int r) {
	return norm(h[r] - mul(h[l], pw[r - l]));
}

inline bool eq(int i1, int i2, int l) {
	if(i1 == i2) return true;
	return getHash(i1, i1 + l) == getHash(i2, i2 + l);
}

int l[N], mx[N];

inline void solve() {
	precalc();
	
	fore(i, 0, n / 2) {
		int c1 = i, c2 = n - 1 - i;
		if(s[c1] != s[c2]) {
			l[i] = -1;
			continue;
		}
		int lf = 0, rg = min(c1, n - 1 - c2) + 1;
		while(rg - lf > 1) {
			int mid = (lf + rg) >> 1;
			
			if(eq(c1 - mid, c2 - mid, 2 * mid + 1))
				lf = mid;
			else
				rg = mid;
		}
		l[i] = lf;
	}
	
	fore(i, 0, n / 2) {
		if(l[i] < 0)
			continue;
		mx[i - l[i]] = max(mx[i - l[i]], 2 * l[i] + 1);
	}
	fore(i, 1, n / 2)
		mx[i] = max(mx[i], mx[i - 1] - 2);

	fore(i, 0, (n + 1) / 2) {
		if(i) printf(" ");
		if(mx[i] == 0) mx[i] = -1;
		printf("%d", mx[i]);
	}
	puts("");
}

int main(){
	if(read()) {
		solve();
	}
	return 0;
}

961G - Partitions

Разбор

Решение (adedalic)

#include <bits/stdc++.h>

using namespace std;

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)

const int MOD = int(1e9) + 7;

inline int norm(int a) {
	while(a >= MOD)
		a -= MOD;
	while(a < 0)
		a += MOD;
	return a;
}

inline int mul(int a, int b) {
	return int((a * 1ll * b) % MOD);
}

inline int binPow(int a, int k) {
	int ans = 1;
	while(k > 0) {
		if(k & 1) ans = mul(ans, a);
		a = mul(a, a);
		k >>= 1;
	}
	return ans;
}

const int N = 200 * 1000 + 555;

int f[N], inf[N];

void precalc() {
	f[0] = inf[0] = 1;
	fore(i, 1, N) {
		f[i] = mul(f[i - 1], i);
		inf[i] = mul(inf[i - 1], binPow(i, MOD - 2));
	}
}

int n, k, w[N];

inline bool read() {
	if(!(cin >> n >> k))
		return false;
	forn(i, n)
		cin >> w[i];
	return true;
}

inline int c(int n, int k) {
	if(k > n || n < 0) return 0;
	if(k == 0 || n == k) return 1;
	
	return mul(f[n], mul(inf[n - k], inf[k]));
}

inline int s(int n, int k) {
	if(n == 0) return k == 0;
	if(k == 0) return n == 0;
	
	int ans = 0, sg[2] = {1, MOD - 1};
	forn(cnt, k)
		ans = norm(ans + mul(sg[cnt & 1], mul(c(k, cnt), binPow(k - cnt, n))));
	return mul(ans, inf[k]);
}

inline void solve() {
	int sum = 0;
	forn(i, n)
		sum = norm(sum + w[i]);
		
	int s0 = s(n, k);
	int s1 = mul(n - 1, s(n - 1, k));
	
	cout << mul(sum, norm(s0 + s1)) << endl;
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
#endif
	precalc();
	
	assert(read());
	solve();

#ifdef _DEBUG
	cerr << "TIME = " << clock() << endl;
#endif
	return 0;
}

Комментарии (48)

Показать архивные | Написать комментарий?

Mohinem

7 лет назад, # |

← Rev. 2 →

Damn, I used Order Statistics tree to solve Problem E after the contest, and now I find it can be done with BIT.

http://codeforces.net/contest/961/submission/36984273

→ Ответить

ghoshsai5000

7 лет назад, # ^ |

Can you explain your approach ?

pk842

nice problemset :)

Had solved E in 3 hours by using persistence segment tree. By seeing the editorial i think that i know nothing :)

Nice editorial!

dalt

I solved E with persistence segment tree too, but it didn't took too much time because the only difference between normal segment tree and persistence segment tree is that you have to change the update process of later.

Naumtsev

It's beautiful problemset, thx!

michaelw12

Geomety always seems to get me..

lincoln17

Can someone give me more detailed explanation of question B?

shouryap

First, in O(N) time, we can calculate "total", the current total number of theorems that Mishka will be able to write without the secret technique.

Now we calculate the EXTRA number of theorems (apart from the ones for which Mishka needs no help) that Mishka will be able to write if the secret technique will get used at the first minute; this is O(K) of course. Call this number "cumu". Now in O(1) time, we can find out the number of theorems that Mishka can write down if the secret technique will get used at the second minute (just remove the number of theorems for the first minute (if applicable) and add the number of theorems for the (K+1)th minute (if applicable)). Keep "sliding" till you reach the end. Of course, maintain a maximum of what you have seen so far, which we call maxcumu.

Finally, add "maxcumu" to "total". http://codeforces.net/contest/961/submission/36992860

CODENT47

I used just the priority queue and AVL for E and it just worked fine. In min priority queue I save pair of (ai,i). On reaching i+1 I pop all those ai from priority queue where aj<i+1 (j<=i) because they can't pair with further seasons. Now I need to find those indices which are in priority queue and are less than a(i+1) because if index is greater than a(i+1) it won't be able to pair with season(i+1). For doing this I use an AVL. Whenever I am popping from priority queue I delete the corresponding index from AVL. I then count all indices lesser than (ai+1) and it to my final answer. Then finally I insert the pair (a[i+1],i+1) to priority queue and index i+1 to AVL. (Both operations take LogN complexity). It was much easier to code and code for AVL is easily available on GFG. My Solution

gardusig

I have made the same, but with Fenwick tree (BIT), much more simple to code.

Baliuk

Nice F

OptxPrime

Amazing problemset. I solved E after the contest using merge sort tree, it was pretty intuitive, and good oportunity to learn to code merge sort tree (because i didnt implement it before, only knew idea). Anyone else solved it this way?

arjun17

Yah ! I also sloved it using merge sort tree.

Just_code_it

Can anyone help me in understanding Problem E?

Fayaz

Observe that for some season i we'll only get a collision with an episode of season j where j < i if a_j >= i and a_i >= j. So we just need to able to answer for a particular season i how many seasons with index j such that j < i have a_j >= i and a_i >= j. We can do this query for all i (using a merge-sort tree for example) and then report the answer.

di_z

For E, just use BIT to maintain sorted segments. Then use binary search (lower_bound in C++) to get the answer in each segment. I think it's the most simplest approach (or the best answer especially in a time highly limited competition).

Here is my code 36971807

Most of the shortest answers are done by this way.

Could you elaborate on your method? Looks interesting

Well. In this problem, we need to calculate how many numbers are greater than i in the range [i + 1, a[i]].

Let d[l, r, x] denote how many numbers are greater than x in the range [l, r].

Obviously, d[l, r, x] = d[1, r, x]-d[1, l-1, x] (prefix sums)

Then you can use Binary Indexed Tree (BIT) with vector, which means each node of the BIT is a vector that collects numbers in a range, just like the node of a typical BIT sums numbers in the range.

After sorting each vector, you can use binary search to get answers in each vector. By using BIT query method, you can form prefix sums and get d[l, r, x].

floatingp_p0int

What will be the complexity of this solution? Like if You sort vectors in every node of BIT? Won't it be too much? Further, what will be the max size of a any vector representing a node?

Each number appears in O(log n) vectors. So the space complexity is O(n log n). Time complexity is O(n log^2 n).

Well, the max size of a vector is O(n). However, the average size of vectors is just O(log n).

CSQ31

4 года назад, # ^ |

nice approach :)

kanak893

For problem D what would be the approach if maximum number of lines allowed were 3?

← Rev. 3 →

This is one thing I could think of; I am sure we can do better. Assume n >= 4, and assume that the n points lie on 3 lines. Consider any four points (say, the first ten points given). By Pigeonhole Principle, some 2 points lie on the same line. And well, take all cases. Once you are done finding one of the lines, the problem reduces to the given problem.

Another less "casework" way considers n>= 10. Consider the first 10 points. Again by Pigeonhole Principle, some 4 points lie on the same line, and (I guess) we can also prove that if four points are collinear, then one of the lines must pass through them. So just find a quadruple of points that are collinear. If there does not exist a quadruple, then our assumption is false, otherwise the quadruple determines one line, and the problem has been reduced to D.

tribute_to_Ukraine_2022

Another solution which can be easily generalized for more than two lines is: pick two different points at random, remove them and all points collinear with them and repeat until you have drawn expected number lines, and repeat the whole process until you have found way to partition all of the points or until clock() < TIME_LIMIT * CLOCKS_PER_SEC. Suppose pn points lie on first line and qn on the second (p + q) = 1 then probability of choosing points lying on the same line is roughly p² + q² which is greater or equal to $\text{[math]}$ ). In case of 3 lines we have at least $\text{[math]}$ chance for our first guess and at least $\text{[math]}$ for our second guess. which is total $\text{[math]}$ (or for k lines $\text{[math]}$ ). 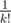For k ≤ 5 this should be enough.

2014CAIS01

+10

But the random can be hacked in open hacking……like 36960802

It can't be if I seed random number generator with the hash of the input. Or at least hacking it would be much more difficult.

rishabhach

Can anyone help me in understanding Problem c?i am not getting tutorial too.

Ghost0fSparta

We have 4 pieces of board so to make a new chessboard out of the 4 we need 2 pieces with black cell on the (0,0) position and 2 pieces with white cell on the (0,0) position. Also note that once we know the color of (0,0) position we can make the whole chessboard out of it. So we find the cost of converting each piece into two chessboards — one with white cell at (0,0) and another with black cell at (0,0) and then we calculate the minimum of all possible ways.
My solution

desert97

Just wanted to mention that F is essentially the same (actually more explicit) as an old POI problem: https://main.edu.pl/en/archive/oi/19/pre

kjain1810

How to solve problem D for N points and K lines?

Blue233333

+34

Something about Problem G. I guess most of us get the formula below easily:

$\text{[math]}$

But the Editorial above claims:

So may anybody prove that:

adedalic

I would gladly hear the formal proof of equation myself since it doesn't sound like easy transformation.

← Rev. 6 →

Here is a proof I thought of. Also, sorry for too many revisions :P

Consider n students who wish to participate in a contest. They must enter themselves in exactly k non-empty groups. One of these groups is a special group who gets to participate in Div 1, while the others participate in Div 2. Furthermore, Alice, one of the students, is very good at coding, so she will always participate in Div 1. Furthermore, the special group has a team leader. We count the number of ways C of partitioning the students in two ways.

First, we select, out of n - 1 students, j - 1 students who, along with Alice, form the special group. This can be done in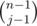 $\text{[math]}$ ways. Now the n - j normal students can be partitioned in 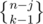$\text{[math]}$ ways, and the team leader of the special group can be chosen in j ways. Thus $\text{[math]}$ .

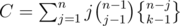Another way is this: Suppose Alice is the team leader. Then simply partition the n students into k groups in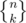 $\text{[math]}$ ways, and the team Alice belongs to is special. Otherwise choose a team leader out of the remaining students in n - 1 ways (call this chosen leader Bob), and partition the n - 1 students other than Bob in 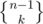$\text{[math]}$ ways. The one Alice belongs to is the special group, so Bob belongs to that group of course. Therefore $\text{[math]}$ .

+14

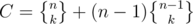Yes, you are right, but you make exactly what problem G asks. Your proof is just a more formal than from editorial. In other words, formulas are same because they count same thing.

What I (and probably, Blue233333) expected are just formal equivalent transformations of left and right parts using some properties of Binomial Coefficients and Stirling numbers.

With swm_sxt and zsnuo's help, I find an approach to use equivalent transformations to prove that, but I am still a little confused.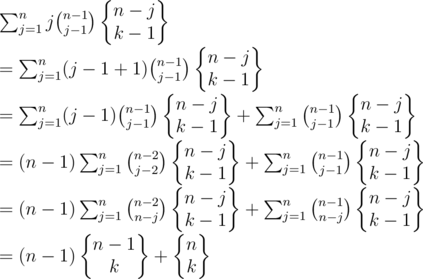 $\text{[math]}$

However, I don't understand the last step's formula transformations very clearly, while I could only understand it with this: Dividing n people into k non-empty groups, means that we first choose j, 0 ≤ j ≤ n - 1, people to be members of person n's group, and then divide the remained persons into k - 1 groups.

jslijin

6 лет назад, # ^ |

You can check it at wikipedia.

gooooooogol

There are n circles drawn on a piece of paper in such a way that any two circles intersect in two points, and no three circles pass through the same point. Turbo the snail slides along the circles in the following fashion. Initially he moves on one of the circles in clockwise direction. Turbo always keeps sliding along the current circle until he reaches an intersection with another circle. Then he continues his journey on this new circle and also changes the direction of moving, i.e. from clockwise to anticlockwise or vice versa. Suppose that Turbo’s path entirely covers all circles. Prove that n must be odd.

This is from IMO. Also, it is unrelated.

can someone please explain me F. I didn't get the editorial :(

6 лет назад, # |

Here is my blog post on the very elegant geometry problem D :)

Noob_Noob_

i feel like my brain expanded after solving E xD

-osdajigu-

4 года назад, # |

← Rev. 4 →

I would like to share my solution for problem F.

Given a string s let's create a new string t of double size concatenating the first character with the last character, the second with the penultimate, and so on.. For example, given ababab we got abbaabbaabba

If you look carefully at this new string, we are now interested in palindromes! (convince yourself about this). Of course, we are not interested in all palindromes but some of them. More precisely we are interested in the palindromes that meet these requirements (Let L be the beginning of the palindrome, R the end, and n the length of the original string):

L is an even position
R is an odd position
L is in the first half of the string (this is because is symmetric)
(R-L+1)/2 is odd (this is a requirement of the problem)
n-R/2-1 > L/2 (is not a proper prefix-suffix)

So we can iterate over all the biggest palindromes and then just calculate the answer for each substring and propagate the answer to small ones.

The solution is O(N);

Here is the link to my submission

bmerry

3 года назад, # |

I realise this is an old contest but I'm just trying it now. Is test case 34 on F some sort of anti-hashing hack? I tried a polynomial rolling hash with three different (prime) values for x, all working mod 2^64, and they all fail on this case (here, here and here). When I changed the modulus to 10^9+7, it passed, even though this gives a far smaller range of possible hash values.

hos.lyric

3 года назад, # ^ |

I somehow happened to solve a problem in this round, to notice your comment :)

The case looks to be the famous one: https://codeforces.net/blog/entry/4898. In short, the polynomial is something like $$$(1 - x) (1 - x^2) (1 - x^4) (1 - x^8) \cdots$$$ and any odd $$$x$$$ makes it divisible by $$$2^{64}$$$. For a prime modulus, we can have a probability bound from the fact that a non-zero polynomial of degree $$$n$$$ has at most $$$n$$$ roots (Schwartz–Zippel lemma).

Thanks, I learned something new.

MuhammadSawalhy

2 года назад, # |

I had a problem with D, test case 49 seems YES to me but the wanted answer is NO. All the points lie in the same line.

All the lines passing throw $$$p[i]$$$ and $$$p[0]$$$ (where $$$1 \le i \le 5$$$) are with the exact same slope $$$1.61803398875$$$.

Here are the points plotted with Desmos

My submission: 172444322

2 года назад, # ^ |

The solution passed when I got rid of all double in the code. What I learned here is to think about doubles as monsters that will eat so I have to run away.

Wayne_Yan

22 месяца назад, # |

The link for the alternative solution of problem F is broken. Here's the link: https://codeforces.net/blog/entry/58707?#comment-423461

Блог пользователя vovuh