Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 165 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
| Название |
|---|



Автокомментарий: текст был обновлен пользователем fcspartakm (предыдущая версия, новая версия, сравнить).
Auto comment: topic has been updated by fcspartakm (previous revision, new revision, compare).
For C if the number of digits was greater is there any way we can solve it?
We can, in O(2^n * n), if n is the number of digits, brute force every possible sequence of deletions, and then check if the string we have got left is a square or not.
My bad lol XD
Can we solve in it polynomial time complexity?
We can solve it in O(sqrt(n) " log(n)), log in base 10.
If d is the number of digits of N, then 2d × d = N × logN.
You can do it in straingforward way in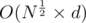 just loop over square root and check is it the answer or not, which is definitely better, when
just loop over square root and check is it the answer or not, which is definitely better, when 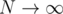 .
.
You're right; I only saw that my solution would work for N <= 10^18, while this one wouldn't.
But asymptotically the sqrt() one is better, whoops.
I'm sorry. I am not able to understand this.
I have coded both solutions. Here is the bitmask solution and here is the other solution.
When we use bitmasks, we can extend the solution to 18 digits.
But, we cannot extend the other solution to 18 digits as we'd have to check 10^9 squares.
Can you please explain why asymptotically the other solution is better ?
Actually I don't even know anymore. I'm really bad at maths. I just tried calculating for some really large N (like, 500 digits), and the bitmask solution is still better there, so it's probably the better solution. My bad
I think it's because above analysis for bitmask solution isn't tight enough.
Let d be the number of digits, then d is about log10N.
The bitmask solution runs in O(d * 2d) worst case time.
O(d * 2d) = O(d * 2log10N) = O(d * Nlog102) = O(d * N0.302)
(log10 2 is about 0.301)
which is better than the running time of square root method O(d * N0.5) asymptotically.
I think the difference comes from the fact that one cannot say O(22N) = O(2N). (Intuitively 22N is square of 2N) Similarly, d =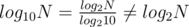 , when taking 2d, ignoring the constant factor
, when taking 2d, ignoring the constant factor 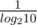 gives an asymptotically loose bound.
gives an asymptotically loose bound.
So, it is reasonable that an O(N0.302 * logN) solution works for N = 1018, while an O(N0.5 * logN) solution doesn't.
Я не олимпиадник, но для G первое что приходит на ум это обычная сканирующая прямая. Выделим только горизонтальные отрезки. Причем в силу того, что известен обход многоугольника мы можем легко определить пересекая граней мы будем входить или выходить из многоугольника. Так же уже на стадии заполнения массива можно обрезать отрезки по x. Если оба конца больше или меньше х окна, можно подобные отрезки игнорировать. А те что выходят частично обрезать. Запишем в массив y и x1,x2 отрезка и тип отрезка (вход/выход). Отсортируем по y. Будем сканировать по y. При этом до окна будем просто объединять/вычитать/разделять на две группы отрезки, а после входа в окно будем при объединении и разрезании отрезков хранить их группу (СНМ). Если при вычитании отрезка, грань вырождается то увеличим кол-во многоугольников. Как только y выйдет из окна добавим к кол-ву многоугольников кол-во оставшихся групп в СНМ.
Сканируем снизу вверх.
Зеленым цветом начальное множество отрезков на входе в окно. Фиолетовым объединение множеств. Оранжевым вычитание части множества. Голубым удаление из множество (добавляем единицу к видимым многоугольникам). Желтым множества оставшиеся при выходе из окна. Ответ на задачу это кол-во голубых и желтых множеств.
Обожаю русскоговорящее сообщество, за что хоть минусы ? картинка не понравилась ?
Решение с этой логикой
JFYI пока это решение с наименьшим потреблением памяти и временем работы. Еще раз спасибо за минуса :).
Никто не доверяет нерейтинговым аккаунтам, поэтому и минусы.
Please add this link to the contest materials. Right now, it is very hard to find.
In Problem E :“It is technically possible to connect the cities a and b with a cable so that the city c (a<c<b) is not connected to this cable”
Does this mean if a-b has an edge then a can't connect to c where a<c<b ?
No, it means that if you have three points A < B < C then it's allowed (not necessarly) to connect A and B with a cable without connecting C with them (but you can connect if you want A-B and A-C)
got it Thanks
Ur welcome
Problem G can be solved using horizontal scanline and counting horizontal segment groups using dsu. just like rendering in CG. Solution
Thank you. It's helpful for me.
can someone please explain this part of F : " Now, it is sufficient to the answer to take such paths plus the corresponding reverse edge that do not intersect with others (that is, the size of the DSU component is 1):"
Consider a back-edge (u, v) and the corresponding cycle u, p1, ..., pk, v. Let's suppose that this is the first back-edge we process. Following the code from the editorial, after processing this cycle we see that leader(pi) = leader(pj) = v for all i, j. Note that we exclude u. This is done to exclude situations like articulation points that belong to more than one simple cycle.
Let's now take into account this part of the code:
And the statement you do not understand:
Now, it is sufficient to the answer to take such paths plus the corresponding reverse edge that do not intersect with others (that is, the size of the DSU component is 1)
Let's consider again our cycle u, p1, ..., pk, v. If our graph had only this back-edge then we see that all the edges from the cycle belong to exactly one simple cycle, as another back-edge would be needed to have at least one additional cycle. However, imagine these two following cases:
sizes[leader(v)]++will be executed twice. With this we know that at least the edge (v, par(v)) belongs to more than one cycle, which implies that all the other edges from the cycle (plus some other ones) also belong to more than one cycle.sizes[leader(v)]will be again at least two. In fact, this is the same as case 1, but I wanted to illustrate it better. At least the edge (pi, par(pi)) belongs to more than one cycle, which implies that the other ones will do, too.Note that you do not need to care about vertices that do not form part of any simple cycle, as they will not appear (if they did, this means that you have reached them by iterating the endpoint of some back-edge, which means that they belong to a cycle, which is a contradiction).
With this criteria you can safely take all the edges obtained by iterating some lower endpoint of a back-edge (u, v) such that sizes(leader(v)) = 1
Thanks for the reply! If you don't mind can you please answer a few questions:
"This is done to exclude situations like articulation points that belong to more than one simple cycle." Can you please elaborate this. Why this helps? because that point may be any one of (p1, p2, ....).
I even didn't understand the time complexity of the solution. I had implemented brute force solution before (looping in each cycle and incrementing count of each edges on the go and checking count at the last). But it times out. code. Here also we are looping on each of the cycle. So, how it is working?
I know i'm missing something. So, please don't mind if you find these question silly. Thanks a lot :)
About the articulation point statement: it was an example. Anyway, being more precise, if the articulation point belongs to the sequence p1, ..., pk, v then there is no problem. Also, if this situation happens, it is guaranteed that it will happen exactly once. The articulation point will necessarily appear as the root of any other cycles. Consider this example:
Suppose that your DFS starts at 3 and you get the sequence 3, 1, 4, 5. As you can see, the fact that 1 is labeled the same as the rest of vertices is not problematic. However, it must be excluded from the other cycle in order to avoid joining two disjoint simple cycles.
About the cost:
Let's break down the editorial's code and comment the pieces.
This is a classic DFS. We visit all vertices exactly once, so this is linear. So, our verdict is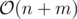
This one is tricky. Let's first pretend that this part does not exist:
If this last loop was not present the code would run in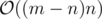 . Supposing that our graph consists of a single connected component, we see that only a linear amount of edges won't be back-edges in our DFS tree. So if we have a quadratic amount of edges (e.g: complete graph) we will execute the cycle reconstruction phase a quadratic amount of times, this is bad!
. Supposing that our graph consists of a single connected component, we see that only a linear amount of edges won't be back-edges in our DFS tree. So if we have a quadratic amount of edges (e.g: complete graph) we will execute the cycle reconstruction phase a quadratic amount of times, this is bad!
However, let's think about the last loop:
This part of the code guarantees us that we will never traverse the same path twice. Let's consider the sequence of vertices u, v, s, t such that there is a back-edge (u, t), par(t) = s, par(s) = v, and par(v) = u. This magic loops ensures that par(t) = par(s) = par(v) = u after processing the path. Great! Note that the length of the longest path in any DFS tree is at most n - 1. These two facts (we never revisit + length of longest path) makes the code run in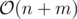 .
.
And now let's consider the last part of the code:
This is tricky again, as you may think something like "hey, this code can potentially run in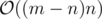 because any back edge can potentially trigger the inner loop!". Actually, it does not. Note that we only process sets such that they have exactly one simple cycle. The direct implication of this fact is that these sets will surely be disjoint (if they were not, any edge would belong to more than one cycle, which is precisely what we are avoiding!). Given that we have at most n vertices, this code is also
because any back edge can potentially trigger the inner loop!". Actually, it does not. Note that we only process sets such that they have exactly one simple cycle. The direct implication of this fact is that these sets will surely be disjoint (if they were not, any edge would belong to more than one cycle, which is precisely what we are avoiding!). Given that we have at most n vertices, this code is also 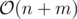 !
!
Thanks a lot for such a nice explanation.
Can someone explain me Problem G? I don't understand how am i supossed to use that planar graph to count areas belonging to the polygon and how to orientate edges to know which one are "important".
Can someone explain how below given TestCase in Problem E has answer 54 ??
8
-12 P
-9 B
-2 R
-1 R
2 B
8 B
9 R
15 P
We don't have any red or blue vertices before the first purple city and after the last purple city so we just have to calculate how to connect cities between that pair of purple cities. Using the first method we can have roads (-12P, -9B, 2B, 8B, 15P) and (-12P, -2R, -1R, 15P) and that way we have connected both red cities with purple cities and blue cities with purple cities but the total lentgh is basically twice the distance between purple cities which is 2*(15-(-12))=54
just connect all the 'b' and 'p' linearly(cost = 27) and similarly all the 'r' and 'p' (cost = (15 — (-12)) i.e. 27. So, 54.
For E, can someone explain why this works? This is a greedy algorithm without proof.
Go through this article : https://arxiv.org/pdf/1603.00580.pdf
What does carcass mean which is mentioned in the editorial of
962F-Simple Cycle Edges? It seems that it has some specific meaning in a graph. Does it mean something like a spanning tree?I know it's been a while, but did you figure out what carcass meant?
Is Problem E exactly the same as Problem F from Good Bye 2017?
http://codeforces.net/contest/908/problem/F
Yes, you are right.
В задаче С сказано "перебрать с помощью масок". Что такое маски, если можно то скиньте ресурс на котором можно про них почитать.
What is the time complexity of D. I guess it is not N * log(N) because a particular index might be added and removed more than once
In F, how is this claim even true?
It is easy to see that if an edge belongs to exactly one cycle from the fundamental set of cycles, then it belongs to exactly one simple cycle.
Consider a graph, which is gluing two cycles with one edge in common. Those two cycle can be the fundamental set of cycles, and thus all edges other than the glued one appear in one fundamental cycle, but none of the edges belong to exactly one simple cycle.
The correct claim is: Find any fundamental set of cycles. Any edges belongs to exactly one simple cycle if and only if it belongs to a fundamental cycle that does not intersect any other fundamental cycle. Somehow the editorial wrote a totally wrong statement and still followed the correct way.