Adiv2. Рассмотрим массив A целых чисел от 1 до nk. Удалим из него все числа ai, а все, что осталось, запишем в массив B. Массив B будет состоять из (n - 1)k элементов. Теперь для i-го ребенка следует вывести числа ai, B[(n - 1) * (i - 1) + 1], B[(n - 1) * (i - 1) + 2], ... B[(n - 1) * (i - 1) + n - 1] (индексация B начинается с 1).
Автор — Gerald .
Bvid2. Решение 1. Напишем перебор по всем числам, состоящим из не более чем 9 цифр (число 109 преверим отдельно). Схематично это будет выглядеть так:
dfs( int num ) // запускать как dfs(0)
if (num > 0 && num <= n) ans++
if (num >= 10^8) return
for a = 0..9 do
if num*10+a>0 then
if число num*10+a содержит не более 3х цифр then
dfs( num*10+a )
В ans теперь будет находиться ответ. Напишем, запустим — увидим, что работает быстро (это решение выполняется одинаковое время на всех тестах). Отошлем.
Решение 2. Будем строить все безусловно счастливые числа с помощью битовых масок. А именно: переборем длину числа L, пару цифр x и y, а так же битовую маску m длины L. Если i-ый бит m равен 1, то в i-ый разряд поставим x, иначе y. Итого будет сгенерировано порядка 103 × 210 чисел (это очень грубая оценка, можно показать, что их будет раз в 10 меньше).
В этом решении нужно аккуратно обрабатывать случаи ведущих нулей и случая, когда число состоит из одинаковых цифр.
Автор — Gerald
Adiv1, Cdiv2 Давайте посмотрим как будет меняться функция f на всех суффиксах последовательности a. Значения f будут расти с увеличением длины суффикса, причем при каждом увеличении все единичные биты так и останутся единицами, а некоторые нули перейдут в единицы. Таким образом, произойдет не более k увеличений, где k — число бит (в данном случае k = 20). То есть среди всех суффиксов будет не более k + 1 различных значений f.
Теперь мы можем просто идти по массиву a слева направо и поддерживать в массиве m (или в сете) значения f для всех подотрезков, заканчивающихся в текущей позиции (его размер никогда не будет превышать k + 1). При переходе из позиции i - 1 в позицию i мы заменяем m = {m1, m2, ..., mt} на {ai, m1|ai, m2|ai, ... mt|ai}, после чего удаляем повторяющиеся значения (в случае сета сет все делает за нас). После этого новые значения отмечаем в глобальном массиве флагов (или запихиваем в глобальный сет). В конце выводим количество найденных значений.
Bdiv1, Ddiv2 Для каждого ребра будем проверять может ли оно быть телом гидры. Зафиксируем какое нибудь ребро (u, v) (порядок вершин в ребре имеет значение, т.е. потом еще нужно будет проверить ребро v, u). Теперь нам нужно выбрать подмножество из h вершин, соединенных с u, и подмножество из t вершин, соединенных с v (u и v в них, конечно, не должны входить). Сложность заключается в том, что эти 2 множества не должны иметь общих вершин.
Если 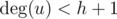 или
или 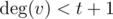 , то тут гидры, очевидно, нет.
, то тут гидры, очевидно, нет.
Иначе, если 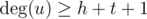 или
или 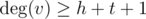 , то тут гидра всегда найдется — даже если все соседние к u и v вершины общие, их количества хватит, чтобы все нужным образом поделилось.
, то тут гидра всегда найдется — даже если все соседние к u и v вершины общие, их количества хватит, чтобы все нужным образом поделилось.
Иначе, остается случай 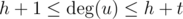 и
и 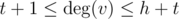 . Тут можно найти общие соседние вершины за время O(h + t), работая с массивом флагов. Когда общее подмножкство вершин найдено, проверить наличие гидры несложно. Поскольку h и t маленькие — проверка будет работать быстро.
. Тут можно найти общие соседние вершины за время O(h + t), работая с массивом флагов. Когда общее подмножкство вершин найдено, проверить наличие гидры несложно. Поскольку h и t маленькие — проверка будет работать быстро.
UPD Как найти общие вершины за O(h + t) при помощи массива флагов? Просто в самом начале заведем булевый массив длины n. Затем при каждой проверке будет сделать следующее. За 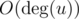 отметим в массиве всех соседей u. После этого посмотрим всех соседей v за
отметим в массиве всех соседей u. После этого посмотрим всех соседей v за 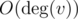 и те вершины, для которых в массиве флагов стоит true, будут являться общими. Когда множество общих вершин найдено, почистим массив флагов за
и те вершины, для которых в массиве флагов стоит true, будут являться общими. Когда множество общих вершин найдено, почистим массив флагов за 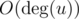 : просто еще раз пройдемся по соседям вершины u. Поскольку
: просто еще раз пройдемся по соседям вершины u. Поскольку 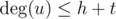 и
и 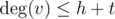 , получим итоговую оценку O(h + t).
, получим итоговую оценку O(h + t).
Итого за время O(m(h + t)) будет найдено ребро, которое должно быть телом гидры, или будет установлено, что гидры в графе нет. За дополнительное время O(m) можно построить саму гидру.
В этой задаче есть решение за 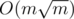 , которое не зависит от h и t, однако это решение сложнее.
, которое не зависит от h и t, однако это решение сложнее.
Автор — Ripatti
Cdiv1, Ediv2 Сначала промоделируем все перемещения дяди Вани "вхолостую". Пусть он побывал в точках (x0 + 1 / 2, y0 + 1 / 2), (x1 + 1 / 2, y1 + 1 / 2), ... , (xn + 1 / 2, yn + 1 / 2). Интересными для нас координатами по оси x будут x0, x0 + 1, x1, x1 + 1, ... xn, xn + 1, по оси y — y0, y0 + 1, y1, y1 + 1, ... yn, yn + 1. Добавим к этим координатам границы поля.
Построим "сжатое" поле: каждая клетка этого поля обозначает прямоугольник изначального поля, находящийся между двумя соседними интересными координатами. Размер этого сжатого поля будет порядка O(n) × O(n). Пусть изначально все клетки поля белого цвета. На этом сжатом поле промоделируем все перемещения еще раз и покрасим черным цветом все обработанные ядом клетки. Каждое перемещения затронет O(n) клеток, поэтому все перемещения смоделируются за O(n2).
Теперь промоделируем действия жуков. Запустим поиск в глубину (или поиск в ширину) и зальем красным цветом все клетки, которые будут съедены жуком.
Теперь еще раз пройдемся по сжатому полю и просуммируем площади прямоугольников, соответствующих черным и белым клеткам. В итоге получим ответ.
Итого решение за O(n2).
Автор — Ripatti
Ddiv1 Нам нужно для каждого столбика кубиков узнать высоту самого нижнего кубика, который мы сможем увидеть — все кубики выше него мы тоже увидим.
Посмотрим на город из кубиков сверху — увидим сетку размера n × n. Проведем через каждый узел сетки прямую, параллельную вектору v. Нам интересно только что происходит в каждой из полос между этими прямыми. Каждый столбик покрывает некоторый отрезок из полос длины порядка O(n).
Построим массив a, каждый элемент которого будет соответствовать одной из полученных полос. В этом массиве мы будем хранить максимальную высоту столбика среди всех рассмотренных не текущий момент.
Теперь отсортируем все столбики по расстоянию от наблюдателя и в этом порядке будем выполнять запросы двух видов:
Минимум на отрезке. Нужен нам для того, чтобы определить высоту самого нижнего видимого кубика.
Замена значений на max(ai, h) на отрезке. Это нужно для "рисования" стоблика.
По сути это все решение, дальше только возникает вопрос о структуре данных, которая позволяет быстро выполнять запросы. Возможны варианты: декомпозиция на блоки (длина каждого блока должна быть порядка  , поскольку длины запросов длины O(n); это дает решение за O(n5 / 2)), дерево отрезков (сложность
, поскольку длины запросов длины O(n); это дает решение за O(n5 / 2)), дерево отрезков (сложность  ), тупо массив (заходит если все оптимизировать по кэшу, O(n3)).
), тупо массив (заходит если все оптимизировать по кэшу, O(n3)).
Автор — Ripatti
Ediv1 Будем конструктивно строить матрицу. На каждом шаге у нас будет массив групп столбцов. Порядок групп определен, однако порядок столбцов внутри группы — нет.
Строки можно менять местами как нам угодно, поскольку это не влияет на ответ.
Опишем процесс построения матрицы. Сначала найдем строку, в которой больше всего единиц. Поменяем ее местами с первой строкой. После этого создадим две группы. В первую поместим все столбцы, где в первой строке стоит 1, во вторую — где стоит 0. Группа, где собрались 0 — "особенная" (об этом ниже).
Далее будем несколько раз делать следующее: искать строку, для которой хотя бы в 2х группах имеется хотя бы по 1 единице. Для каждой такой строки мы можем однозначно определить положение единиц в ней. Либо определить, что расположить нужным образом единицы в ней нельзя и сразу вывести NO. После того, как положение единиц определено, некоторое группы разделяются на 2 подгруппы.
Следует отметить особенность "особенной" группы — из нее мы можем перекидывать столбцы в самое начало матрицы. Ситуации когда будет непонятно какие столбцы перекидывать, а какие нет не возникнет, поскольку в самом начале мы выбирали строчку с наибольшим числом единиц.
После нескольких повторений описанной выше операции могут закончится строки, для которых все можно однозначно восстановить. То есть для каждой строки единицы находятся не более чем в одной группе. Теперь мы можем просто рекурсивно запустить описанное выше решение внутри каждой группы.
Решение работает за O(n3). Его можно улучшить до  , но этого не требовалось.
, но этого не требовалось.
UPD Существут решение за O(n2), основанное на PQ-деревьях, как сообщил mugurelionut. Подробнее тут.
Автор — Ripatti











Что-то не так с форматированием. В тех местах, где написан автор, его ник не подсвечен и стоят 3 дефиса.
Задача Гидра: Тут можно найти общие соседние вершины за время O(h + t), работая с массивом флагов. Можете объяснить поподробнее?
Берём массив чисел размером n заполненный нулями. Дальше проходим по всем смежным вершинам u и инкрементируем значения в соответствующих ячейках, потом тоже самое для v. Те вершины, в ячейках которых окажется 2, являются общими смежными. Асимптотика, очевидно, будет O(h+t).
Не проще ли вместо целых чисел булеаны? Пробегаем смежные с u и ставим для них true. Затем, пробегаем смежные с v и выводим в ответ, если стоит true.
Только вот как взять массив, заполненный нулями, быстрее чем за O(n)?
Можно сделать так.
Заводим для каждой пары уникальное число cur. Проходим по всем смежным вершинам u и ставим в вышеупомянутый массив cur в соответствующие ячейки. Дальше проходим по всем смежным с v и, если в ячейке стоит cur, инкрементим ответ.
Если изначально массив заполнен нулями, а cur, к примеру, меняется от 1 до 2*m, то проблем возникнуть не должно.
Это слишком сложно. Просто можно сначала пройтись поставить метки. А потом, когда дело сделано, пройтись еще раз и удалить их. Мы же знаем, где они могли бы быть.
Можно и так. Хотя это получается лишний проход, но если константа не важна, получается действительно несложно.
Для кого-то сложно одно, для кого-то — другое. Всё дело в том, кто к чему привык
Да, только когда инкрементируем для массива v, сразу смотрим получилось значение 2, или нет. А то можно получить асимптотику О(n+h+t) лишним пробегом массива.
I'm really new to CF, and i'd like to know if the editorials are both in English and Russian, or if it's up to the person who prepares the Round.
Thank you.
PS: If there is a gentle person who can explain briefly this solutions in English, that would be just Awesome!
на каком сайте можно проверить задачи IZHO — 2012?
Можешь взять архив тут.
А проверяющая система нету?
Could you please explain the O(m*sqrt(m)) solution for Bdiv1 ? (at least briefly — maybe just the main ideas?) It sounds interesting to me...
I can't explain it, but you can sort solutions by Execution Time and find the fastest. Maybe it will help you http://codeforces.net/contest/243/status/B?order=BY_CONSUMED_TIME_ASC
Thanks. I will have a look, but I doubt it that anyone implemented an O(m*sqrt(m)) solution as mentioned in the editorial (i.e. independent of h and t). Moreover, even if anyone did, it doesn't necessarily mean that it would be among the fastest ones (maybe the fastest solutions take advantage of the small limits for h and t).
I was hoping that maybe Ripatti could give us some hints regarding the O(m*sqrt(m)) solution (which could work nicely, for instance, even for large values of h and t).
Here's my solution which has a complexity of O(m*sqrt(m))
We define deg(i) as the degree of vertex i
We choose a value S.
step 1:
we will analysis the complexity of step 1. Note that there wont be more than O(M/S) vertices that satisfies deg[i]>=S
we can check whether pair(i,k) is valid in O(deg(k)) time when vertex i and its neighbours are marked. so the inner loop have a total complexity of O(M). and the marking step is obviously O(N).
so this step have a complexity of M^2/S
we notice that, any solution which satisfies deg(u)>=S or deg(v)>=S will be found in the previous step. So if there exists a solution that hasnt been found yet, deg(u)<S and deg(v)<S holds.
step 2:
obviously the marking step is O(S) and the checking step is also O(S) because deg(u) and deg(v) are both smaller than S
so this step has a complexity of O(M*S).
its obvious that after 2 steps, all (head,tail) pairs have be checked.
the total complexity is O(M*S+M^2/S)
we choose S=sqrt(M) and archives a complexity of O(M*sqrt(M))
implemention: RunID 2602573
Thank you. It was a great explanation. And the nice part is that it's not difficult to implement this solution.
For problem B div1/D div2, can anyone explain how "you can find all common vertices in O(h + t), using array of flags"?
for my first code i used a dumb set intersection which is O((h+t)*lg(h+t)) which is too slow (i know set intersection can be done in O(h+t) ). how do you use array of flags?
you can just use an boolean array, index as the key
i suppose you mean vertex number? but there can be 100000 vertices so initializing the array will take O(100000) for every edge which is too much.
if you dont mean vertex number how do you use index to compare equality? the index of the vertex in an adjacency list tells you nothing about the vertex itself.
err, right, my solution timeout on test case 47. ok, i'm gonna ask the same question here...(facepalm)
Use the boolean array of size 10^5 vertices, but note that for every vertex you are testing as the head of the hydra, you only need to mark its neighbors in that array. Just before you go test another vertex, reset all the neighbors to false. This way you aren't initializing all the vertices every time you look for a hydra.
yeah, i did this, still time out, i sneakingly revere the order the edge, and passed the test.
Bdiv2: Solution 1
@Ripatti: I believe you've made a typo in the pseudocode provided for dfs().
The line: if num*10+a>_9_ then should really be: if num*10+a>_0_ then
see 2587112 for my full solution based on this approach if you'd like.
thank you, fixed
"Adiv1, Cdiv2 Let's see how function f changes for all suffixes of sequence a. Values of f will increase when you will increase length of suffix."
Why is this so? If you have the sequence as (2, 3), the xor will decrease if you increase the length of the suffix?
"For every increase all 1-bits will stay 1-bits, but some 0-bits will be changed by 1-bits."
Again how about the case 3 and 5. The xor increases, but not all 1-bits stay 1-bits. Am I missing something here?
The operation is OR not XOR
Thanks. I spent a lot of time thinking about this problem thinking that the function is XOR. My bad.
I am surprised that PQ trees are not mentioned at all in the editorial as a possible solution for Ediv1. The problem is well known as the "consecutive ones" problem and PQ trees are the standard method (as far as I know) of solving it. In fact, by using PQ trees, the time complexity becomes optimal (i.e. O(n^2)).
Here's the original paper describing PQ trees and their application to the "consecutive ones" problem: http://www.sciencedirect.com/science/article/pii/S0022000076800451# (the PDF was freely accessible when I tried it, but I cannot guarantee that it will stay like that for long)
Unfortunately (for me), I have never implemented PQ trees and trying to understand them (or reinvent them) during the contest was not feasible (not that I didn't try it :) ).
Seems that I invented well known problem)
"Иначе, остается случай и . Тут можно найти общие соседние вершины за время O(h + t), работая с массивом флагов. Когда общее подмножество вершин найдено, проверить наличие гидры несложно. Поскольку h и t маленькие — проверка будет работать быстро."
Для любых h и t существует гидра если
deg(u) + deg(v) - common - 2>= h + t, гдеcommon - количество общих вершин у u и v. Правда не знаю как доказать, но решение, использующее это утверждение зашло :)Can someone explain the bitmask solution(different from the editorial one) of div1A / div2C?
Can someone explain the bitmask solution(different from the editorial one) of div1A / div2C?
can anyone please tell me the bitmask solution of div2 B?
You can see that n < 1e9 will contain 9 digits and it will be made of only two digits so code will look like this
few important points when n == 1e9 then add 1 in the ans since 1000000000(1e9) is not included
make sure that starting char to be stored in ans is not zero
code 87452720
thank you so much!!:)