Thanks for participating in my contest!
It was my first round, I hope you enjoyed.
Editorial:
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










I enjoy this contest very much. I hope I will see you as a problemsetter soon!
D can also be solved with suffix arrays + BWT (see this reference: http://blog.avadis-ngs.com/2012/04/elegant-exact-string-match-using-bwt-2/ ).
First you should know how to do it with suffix arrays, in that you can binary search for first and last entry so you can get all occurrences of a word in log(n) per word.
You can speed this up with BWT to take O(|w|) time for a word w (so total is O(sum of lengths of words) rather than O((number of words) * log(n))). The basic idea is you can maintain an interval on the suffix array which contains a suffix of the pattern, and you reduce this interval's size in constant time every time you add another letter. You can see my implementation here: http://codeforces.net/contest/963/submission/37445232
We can do it using only suffix arrays too. No need for optimization using bwt.my submission: http://codeforces.net/contest/963/submission/37425722
note that BWT normally works with suffix array implementations that sort cyclic shifts, but it's possible to adapt it to work on suffix array implementations which sort suffixes
217800014
motivation: if you want to use BWT along with some existing O(n) suffix array
simulating sorting cyclic shifts by building normal suffix array on
s+skinda defeats the point because of suffix array's large constantI have another solution to problem D with suffix automation + dfs. This is my AC code: submission:37454639(http://codeforces.net/contest/963/submission/37454639)
For string s, we build a suffix automaton(sam), and for each node in sam, we can also know its matching position in string s. For each query, we find the node x in sam which represent string m. By dfs the fail tree of sam, we can get a sequence of the positions of each node in the fail tree of node x. We sort this sequence and traversal it to get the answer.
In the worst case, the complexity of this sulotion is O(N·sqrt(N)·log(N)).
But when I solving this problem, I got a trouble. If I swap line 114 and line 115 in my AC code, I will receive a TLE, I don't know why, maybe the compiling optimize? Can anybody explain, thanks.
maybe UB. try drmemory.
Maybe O(N·sqrt(N)·log(N)) is too large. In test 47, s[]="aaa..a", so the fail tree is a chain. If Pre-order traversal, order[l...r) is increasing before sort. So maybe the compiling optimize make it faser.
You could use an O(n) linear sorting algorithm for an array whose elements are not very large.It could get rid of the "log" time complexity to construct a more fast solution.
I'm getting the exact same issue (131028856 vs 131028872). Not sure why this is, but the problematic piece of code is
std::sort. I changed it tostd::stable_sort(131029036) and it actually ran a bit faster than the first version. This blog has some details about it.PS: Sorry about the necropost
My solution involved precalculating all of a & b. Then finding the sum takes O(n) time. This didn't pass, however I have solved n<10^9 problems with linear time before, is there a general rule as to what time is required? (I'm somewhat new to this)
Z contains only k elements, so you can calculate in complexity O(k)
can't understand "alternating sum " problem's solution . can anybody explain how it works. thanks.
and solve the last line using summation of geometric progression
in second line,second SUMMATION i think it will be=> S (in range from i=0 to i=k-1) = Si*a^(n-i-k)*b^(i+k)
you wrote just Si*a^(n-i-k)*b^(i). if i mistake please help.
my typo, sorry for that, it should be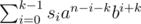
We are basically taking advantage of the periodicity of s. So we first calculate the sum for the first k values.
(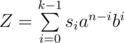 )
)
can be seen as
(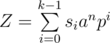 )
)
where (p) is (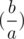 )
)
Then can we multiply this sum by (n+1)/k i.e. number of this periodic strings to get the final result. Not quite. Why?
Because for calculating sum each subsequent periodic substring The power that you raise p will be more. But by how much?- Yes it is k.
Why am i getting a runtime error in testcase 9?
http://codeforces.net/contest/964/submission/38454719
Because you are dividing by zero
Can you explain how you got the exponents in the last term in the second line? How you got a^(k-i-1)*b^(i+n-k+1). And also how you got the last term in the third line from that.
the general thought is to use the peroidicity
Can someone please explain the reason behind why the solution in Destruction Tree Question work ? I am not able to understand the tutorial solution.
My solution is slightly different from the tutorial, but the thoughts are the same.
It is obvious that the answer is `yes' if and only if the tree have odd numbers of nodes. Otherwise it has even nodes, and n - 1 edges, which is odd. Each step we remove even edges, so odd - even - even - ... doesn't equal to 0, hence the edges cannot be removed completely.
And then we use DFS to delete the nodes:
For a node u, DFS(u) does:
Why this method is right? Proof using mathematical induction:
Base case: It is right when the tree has 1 or 3 nodes.
Inductive step:
Case 1: the (sub)tree has even nodes. For convenience we call it subtree u. Because it has even nodes, it must have a parent node (otherwise no solution). After removing u's `even subtrees', there remain even nodes in the tree u(even - even = even). Leaving node u alone, there're odd nodes in the tree u. Since all the even subtrees of u was removed, the remaining subtrees have odd size. odd·odd = odd -> node u has odd numbers of odd-sized subtrees. (odd numbers of odd-sized subtrees) + parent -> the degree of u is even. So we can instantly remove u, and then recursively remove its odd-sized subtrees.
Case 2: the (sub)tree has odd nodes. The proof is very similar with case 1, so omitted.
As shown above, this strategy can remove all the nodes.
Q.E.D.
How can you remove u's even subtree?
Thank you. It is helpful for me.
Thanks a lot. :)
I know a tree with even nodes can not be destructed, but how can you prove that there must exist a solution for an tree with odd nodes?
when size of subtree rooted at u is odd, then suppose c_i will have children of u.
then it can have either odd number of children's[o + o + e], i.e, odd size c_i's will be in pairs or even size c_i's can be in any number. As we want the accumulative sum(SUM) of all c_i's size(size[c_i]) to be even.
More formally size[u] = 1(u itself) + size[c_i]'s.
we know size[u] = odd, so odd-1 = even.
this implies sum of size[c_i]'s = even.
Then removing all even sized c_i will be optimal such that we would be left will even number of odd sized c_i's.
Cannot understand the solution of `Cutting rectangle'... can anyone explain the tutorial for it in detail?
Thanks in advance!
We'd like to combine the rectangles to a big one, and let's call a way to build the big rectangle A GOOD WAY. In a good way, we can move some small rectangles. For example:
It has four types of rectangles and shows a good way. We can also get the same big rectangle in this way:
It can be built by first constructing one part of them, then copy them several times. The Editorial states that every big rectangle contains the same part, like the picture above. More formally, we need to build one BASE PART, such that it contains all types of small rectangles, and the gcd of the numbers of all types in a part is 1. So we need to divide every ci with gcdi = 1 to nci (call it G), and check if base part can be built. If built, we will copy the base part G times to make a bigger rectangle, and the number of ways is the number of divisors of G (copy x times in one direction and y times another,x * y = G). Else, the answer is 0.
The last is how to check the base part. We divide the rectangles into different groups based on their a, and discover that if a way is good, each line's ratio of number of b is the same. For example, when a = 2, [b = 1]: [b = 2]: [b = 4] = 3: 5: 7, and when a = 3, [b = 1]: [b = 2]: [b = 4] must be 3: 5: 7. Based on this we just need to compare some ratios and check if they are the same.
Thanks! a picture says more than thousands of words!
in problem c div2 i want to help how to calculate q when i saw one's solution i found him caculate it by this line long long q=poow(a,k*(MOD-2)%(MOD-1))*poow(b,k)%MOD;
but i can't understand why it calculate in this way as from eq i know that q = (b/a)^k but i can't match this line of code with eq of q can any one help me?
the code is a little weird(may contain typo) but i guess it's modulo inverse?
i got it in this way:
% (MOD-1)sinceq = fastow(b * fastpow(a, MOD-2) % MOD, k)
i have another question in the same problem as i understand all above but i can't understand why i should multiply po(q-1,MD-2)%MD this term but in my answer as i understand from your equation above that the answer if q!=1 : cout<<ans*(po(q,(n+1)/k)-1)%MD; but i found answer: cout<<ans*po(q-1,MD-2)%MD*(po(q,(n+1)/k)-1)%MD; can you help me?!
https://stackoverflow.com/questions/43605542/how-to-find-modular-multiplicative-inverse-in-c
So is that problem 963E a Markov chain?
"Then we can replace all maximum numbers with twos and the rest we split into ones and weight will be the same."
Sorry I'm very new. Can you please explain the solution to Div2 problem A again? I understand every number n > 1 has at least two ways to be partitioned in a strict ordering ([n] and [1,1,1....1]). But what about the numbers in between? Merge a pair of 1's into 2's? Then what do we do about the pairs of 2's? Thank you for your patience.
"Then we can replace all maximum numbers with twos and the rest we split into ones and weight will be the same."
So [4, 4, 2, 1] equivalent to [2, 2, 1, 1, 1, 1, 1, 1, 1]
So we can use only ones and twos.
Can anyone please explain why the Number of different lengths of mi is O(sqrt(M))? And How do we calculate the O(M*sqrt(M))? Many Thanks
Let M = m1 + m2 + ... + mk, then the number of distinct values of mi is O(sqrt(M)), because sum from integers from 1 to 2*sqrt(M) is equal to (2*sqrt(M) + 1)*sqrt(M) > M . Then, for every length Mi, we have O(M) occurrences in the text (note that this is only true because all query strings are different) and since we have O(sqrt(M)) different lengths, total complexity is O(M*sqrt(M)). Just leaving this comment here in case anyone has the same doubt as myself.
My approach in D was a bit different.I used a modified topological sort.I started with a queue and pushed a vertex with even degree in the queue and then just popped a vertex reduced the degree of it's adjacent vertices by one,checked if any of these vertices now have a even degree if so then push this vertex into the queue.I am not able to figure out what is wrong with my approach .Any help is much appreciated. Here is the link to my solution http://codeforces.net/contest/964/submission/37423833 . Thanking you in advance.
5 0 1 1 2 3 Have a try.
My code is giving "NO" and I think no is the correct answer
You can break node 2 first and then break node 3 and finally you got the answer 2 3 1 4 5
In Div 2D/Div 1B, problem tag contains dp. i do not understand how dp is used here. can someone pls explain.
it's tree dp
To late but ==>
dp[i][0] = Is it possible to destroy i-th subtree if we havent deleted the (par,i) edge dp[i][1] = same as above but we have deleted the (par,i) edge
How we update it ==>
so we do a dfs from 1 assume that you're now in vertex start, lets call the neighbours of start that dp[u][0] == false && dp[u][1] == true group 1. and similar call the neighbours of start that dp[u][0] == true && dp[u][1] == false group 2, also call the neighbours of start that dp[u][0] == true && dp[u][1] == true group 3 ( if for some vertex both of them are false the answer is NO).
So now it's obvious that you have to delete all the group 2 before deleting this vertex and similarly you have to delete all of the group 1 after deleting this vertex so now depends on your vertex degree and your DP state (0,1) you have to put some of the group 3 to make it correct ( you can put any vertex of group 3 after or before deletion of this vertex and it doesn't matter)
D can be solved simply by hashing lol
How will you do it, wouldn't it lead to a complexity of O(N^2), because you will have to check every substring of length p where p is the length of M_i for a given query.
Testcase 9 in DIV2C/DIV1A is (a^k/b^k)%mod = 1 but a != b.
Testcase 7 in DIV2D/DIV1B is "root of the tree is not 1" which means p1 is not zero
My solution for DIV2 D/DIV1 B
Deleting a node will toggle the degree of it's neighbours (even becomes odd, odd becomes even)
We find the deepest node that has even degree, delete the subtree of that node in a bfs manner( as all node should have odd degree, when we delete in bfs manner, they become even level by level).
The reason why this is optimal is, we have to delete the deepest node and it's subtree in the above mentioned manner, because if we delete it's parent first then this becomes odd degree and the entire subtree becomes odd. So it is always optimal to delete the deepest even degree node and it's subtree, that will not change the answer
Submission : 91716266
I have no idea why a lot of Codeforces suffix trie/string problem editorials use Aho-Corasick's algorithm, suffix automata, and other fancy structures. Div1D is simpler, actually — the only thing you need is a suffix array.
Okay, so the main idea is that if can find out all the indices for which a query string $$$m_i$$$ appears, then we can just find the set $$$S$$$ of $$$k_i$$$ indices for which $$$\text{max} (S) - \text{min} (S) + s_i.length()$$$ is minimal. If you're not convinced by this, you can think of substrings as intervals and choosing $$$k_i$$$ intervals with minimal union.
Only one question remains: how do you determine the indices from which emanate substrings of $$$s_i$$$? This is kind of a standard trick, but I'll explain anyways. The main idea is that you maintain a suffix array over the original string $$$s$$$. This allows us to find all prefixes of suffixes with given value, since we can just binary search for the range of prefixes of suffixes which correspond to $$$s_i$$$.
The end.
Or is it? There's a little non-trivial aspect to this as well. The complexity may seem to be $$$N^2$$$, since our vector of indices can get massive...right? It turns out that the condition that all the strings are distinct coupled with the fact that the sum of lengths of query strings is small makes the solution passable. I convinced myself that this is true without proving it :(.
Some people bounded the solution at $$$N \sqrt{N}$$$, which seems reasonable, but I don't understand why.