You can download my codes to all problems here.
I will write a full editorial in the next few days. Now you can read hints and short solutions.
750B - New Year and North Pole
750E - New Year and Old Subsequence
750F - New Year and Finding Roots
Also, the solution description of this problem is split into parts hidden in ,,spoiler'' tags. At any moment you can stop reading and try to finish the solution on your own.
750G - New Year and Binary Tree Paths
750H - New Year and Snowy Grid
750A - New Year and Hurry
Do you see what is produced by the following piece of code?
int total = 0;
for(int i = 1; i <= n; ++i) {
total += 5 * i;
printf("%d\n", total);
}
We iterate over problems (a variable i denotes the index of problem) and in a variable total we store the total time needed to solve them. The code above would print numbers 5, 15, 30, 50, ... — the i-th of these numbers is the number of minutes the hero would spend to solve easiest i problems.
Inside the loop you should also check if there is enough time to make it to the party, i.e. check if total + k <= 240.
simple C++ code:24067296
shorter but harder C++ code: 24067301
python: 24067479
750B - New Year and North Pole
Our goal is to simulate Limak's journey and to check if he doesn't make any forbidden moves. To track his position, it's enough to store one variable denoting his current distance from the North Pole. To solve this problem, you should implement checking three conditions given in the statement.
Updating dist_from_north variable is an easy part. Moving ti kilometers to the North increases the distance from the North Pole by ti, while moving South decreases that distance by ti. Moving to the West or East doesn't affect the distance from Poles, though you should still check if it doesn't happen when Limak is on one of two Poles — you must print "NO" in this case.
Let's proceed to checking the three conditions. First, Limak can't move further to the North if he is already on the North Pole "at any moment of time (before any of the instructions or while performing one of them)". So you should print "NO" if direction == "North" and either dist_from_north == 0 or dist_from_north < t[i]. The latter case happens e.g. if Limak is 150 kilometers from the North Pole and is supposed to move 170 kilometers to the North — after 150 kilometers he would reach the North Pole and couldn't move further to the North. In the intended solution below you will see an alternative implementation: after updating the value of dist_from_north we can check if dist_from_north < 0 — it would mean that Limak tried to move North from the North Pole. Also, you should print "NO" if dist_from_north == 0 (i.e. Limak is on the North Pole) and the direction is West or East.
You should deal with the South Pole case in a similar way. Limak is on the South Pole when dist_from_north == M.
Finally, you must check if Limak finished on the North Pole, i.e. dist_from_north == 0.
There were two common doubts about this problem: 1) "Limak is allowed to move 40 000 kilometers to the South from the North Pole and will be again on the North Pole." 2) "Moving West/East may change the latitude (equivalently: the distance from Poles) and this problem is hard 3d geometry problem." Both doubts make sense because they come from misinterpreting a problem as: Limak looks in the direction represented by the given string (e.g. to the North) and just goes straight in that direction (maybe after some time he will start moving to the South but he doesn't care about it). What organizers meant is that Limak should be directed in the given direction at any moment of time, i.e. he should continuously move in that direction. It's a sad thing that many participants struggled with that. I should have written the statement better and I'm sorry about it.
C++ code: 24067685
python code: 24067669
750C - New Year and Rating
We don't know the initial or final rating but we can use the given rating changes to draw a plot of function representing Limak's rating. For each contest we also know in which division Limak was.
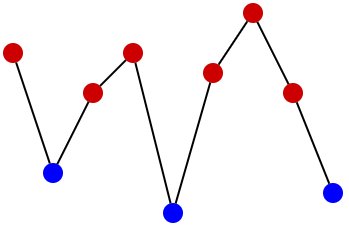
Red and blue points denote contests in div1 and div2. Note that we still don't know exact rating at any moment.
Let's say that a border is a horizontal line at height 1900. Points above the border and exactly on it should be red, while points below should be blue. Fixing the placement of the border will give us the answer (because then we will know height of all points). Let's find the highest blue point and the lowest red point — the border can lie anywhere between them, i.e. anywhere between these two horizontal lines:
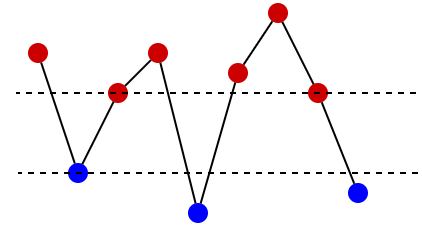
Small detail: the border can lie exactly on the upper line (because rating 1900 belongs to div1) but it can't lie exactly on the lower line (because 1900 doesn't belong to div2).
The last step is to decide where exactly it's best to put the border. The answer will be 1900 + d where d is the difference between the height of the border and the height of the last point (representing the last contest), so we should place the border as low as possible: just over the lower of two horizontal lines we found. It means that the highest blue point should be at height 1899.
There is an alternative explanation. If Limak never had rating exactly 1899, we could increase his rating at the beginning by 1 (thus moving up the whole plot of the function by 1) and everything would still be fine, while the answer increased.
To implement this solution, you should find prefix sums of rating changes (what represents the height of points on drawings above, for a moment assuming that the first point has height 0) and compute two values: the smallest prefix sum ending in a div1 contest and the greatest prefix sum ending in a div2 contest. If the first value is less than or equal to the second value, you should print "Impossible" — it means that the highest blue point isn't lower that the lowest red point. If all contests were in div1, we should print "Infinity" because there is no upper limit for Limak's rating at any time (and there is no upper limit for the placement of the border). Otherwise we say that the highest blue point (a div2 contest with the greatest prefix sum) is a contest when Limak had rating 1899 and we easily compute the final rating.
O(n) code in C++: 24069564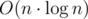 code in C++, with binary search: 24069586
code in C++, with binary search: 24069586
750D - New Year and Fireworks
A trivial O(2n) solution is to simulate the whole process and mark visited cells. Thanks to a low constraint for ti, a backtrack with memoization has much better complexity. Let's understand the reason.
Parts of the firework move by ti in the i-th level of recursion so they can't reach cells further than 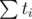 from the starting cell. That sum can't exceed n·max_t = 150. We can't visit cells with bigger coordinates so there are only O((n·max_t)2) cells we can visit.
from the starting cell. That sum can't exceed n·max_t = 150. We can't visit cells with bigger coordinates so there are only O((n·max_t)2) cells we can visit.
As usually in backtracks with memoization, for every state we can do computations only once — let's think what that "state" is. We can't say that a state is defined by the current cell only, because maybe before we visited it going in a different direction and now we would reach new cells. It also isn't correct to say that we can skip further simulation if we've already been in this cell going in the same direction, because maybe it was the different level of recursion (so now next step will in in a different direction, what can allow us to visit new cells). It turns out that a state must be defined by four values: two coordinates, a direction and a level of recursion (there are 8 possible directions). One way to implement this approach is to create set<vector<int>> visitedStates where each vector contains four values that represent a state.
The complexity is 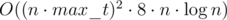 what is enough to get AC. It isn't hard to get rid of the logarithm factor what you can see in the last code below.
what is enough to get AC. It isn't hard to get rid of the logarithm factor what you can see in the last code below.
If implementing the simulation part is hard for you, see the first code below with too slow exponential solution. It shows an easy way to deal with 8 directions and changing the direction by 45 degrees — you can spend a moment to hardcode changes of x and y for each direction and clockwise or counter-clockwise order and then keep an integer variable and change its value by 1 modulo 8. You can add memoization to this slow code yourself and try to get AC.
too slow O(2n) approach (TLE): 24070543
the same code with memoization (AC): 24070548
faster memoization without logarithm (AC): 24070567
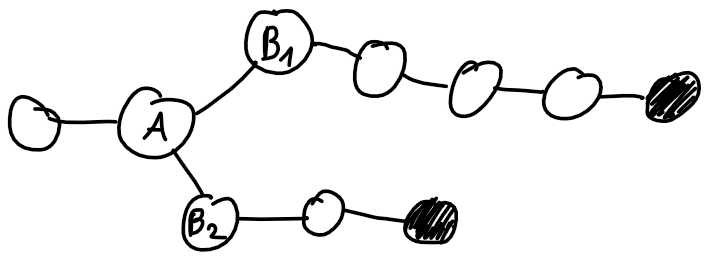
750E - New Year and Old Subsequence
It's often helpful to think about an algorithm to solve some easier problem. To check if a string has a subsequence "2017", we can find the find the first '2', then to the right from that place find the first '0', then first '1', then first '7'. If in some of these 4 steps we can't find the needed digit on the right, the string doesn't have "2017" as a subsequence. To additionally check if there is a subsequence "2016", after finding '1' (before finding '7') we should check if there is any '6' on the right. Let's refer to this algorithm as Algo.
It turns out that the problem can be solved with a segment tree (btw. the solution will also allow for queries changing some digits). The difficulty is to choose what we want to store in its nodes. Let's first use the Algo to answer simpler queries: "for the given segment check if it's nice".
There is only one thing that matters for segments represented by nodes. For a segment we want to know for every prefix of "2017" (e.g. for "20"): assuming that the Algo already got this prefix as a subsequence, what is the prefix we have after the Algo processes this segment. Let's see an example.
TODO
750F - New Year and Finding Roots
750G - New Year and Binary Tree Paths
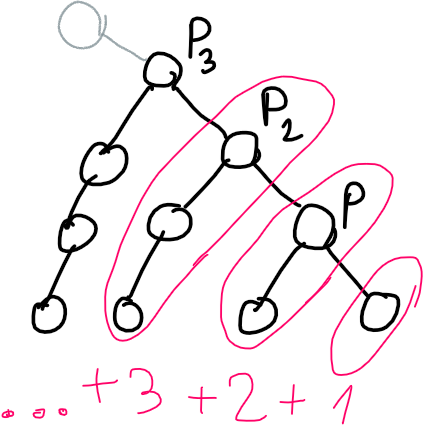
Iterate over L and R — the length of sides of a path. A "side" is a part from LCA (the highest point of a path) to one of the ends of a path.
For fixed LCA and length of sides, let the "minimal" path denote a path with the minimum possible sum of values. In each of the sides, this path goes to the left child all the time:
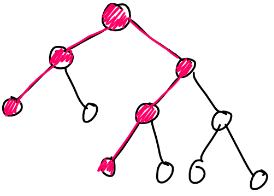
If the LCA is x, the smallest possible sum of vertices on the left side of the minimal path has the sum of vertices:
We can find a similar formula for the minimum possible sum of the right side SR. For fixed L, R, x, the total sum of any path (also counting LCA itself) is at least:
From this, with binary search or just a division, we can compute the largest x where this formula doesn't exceed the given s. This is the only possible value of LCA. Larger x would result with the sum exceeding s. Smaller x would result in too small sum, even if a path goes to the right child all the time (so, the sum is maximized). Proof: every vertex is strictly smaller than the corresponding vertex in the "minimal" path for the computed largest possible x:
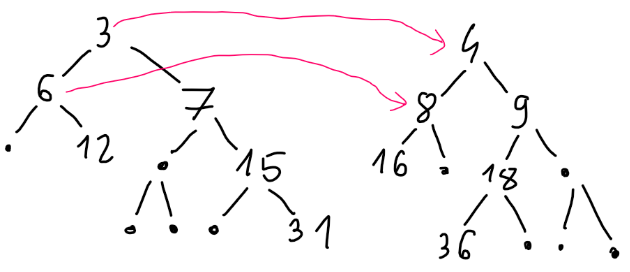
So, from L and R we can get the value of LCA.
Let's assume that the computed value of LCA is 1. For any other value we know that the value of vertex on depth k would be greater by (x - 1)·2k compared to LCA equal to 1, and we know depths of all vertices on a path, so we can subtract the sum of those differences from s, and assume the LCA is 1.
The sum of vertices from 1 to a is 2·a - popcount(a). Proof: if the binary representation of a has 1 on the i-th position from the right, there will be 1 on the (i - 1)-th position in the index of the parent of a and so on. So this bit adds 2i + 2i - 1 + ... + 1 = 2i + 1 - 1 = 2·2i - 1, so everything is doubled, and we get "-1" the number of times equal to the number of 1's in the binary representation of a. Thus, the formula is 2·a - popcount(a).
If endpoints are a and b, the sum of vertices will be 2·a - popcount(a) + 2·b - popcount(b) - 1 (we subtract the LCA that was counted twice). Since popcounts are small, we can iterate over each of them and we know the left value of equation:
Here, s' is equal to the initial s minus whatever we subtracted when changing LCA from the binary-searched x to 1.
The remaining problem is: Given binary lengths L and R of numbers a and b, their popcounts, and the sum a + b, find the number of such pairs (a, b). This can be solved in standard dynamic programming on digits.
To slightly improve the complexity, we can iterate over the sum popcount(a) + popcount(b) instead of the two popcounts separately. The required complexity is 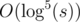 or better.
or better.
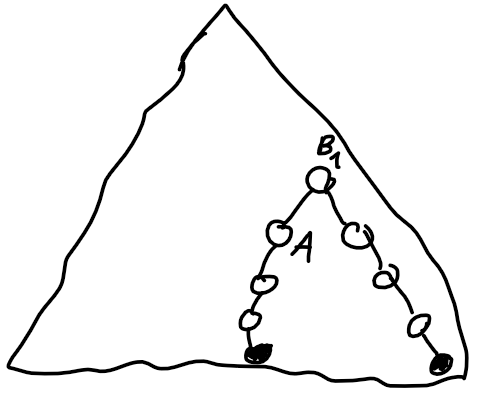
750H - New Year and Snowy Grid
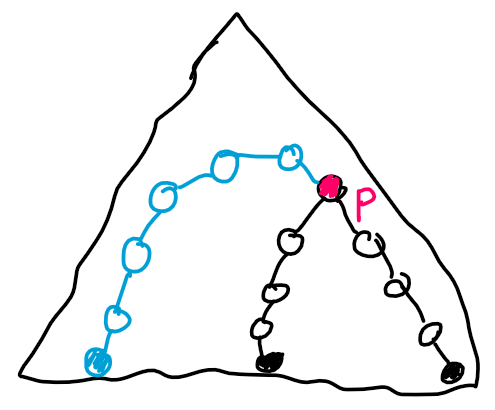
Let's solve an easier problem first. For every query, we just want to say if Limak can get from one corner to the other. He can't do that if and only if blocked cells connect the top-right side with the bottom-left side — this is called a dual problem.
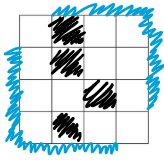
On the drawing above, the top-right side and bottom-left side are marked with blue, and blocked cells are black. There is a path of blocked cells between the two sides what means that Limak can't get from top-left to bottom-right corner. The duality in graphs changes the definition of adjacency from "sharing a side" to "touching by a corner or side" — the black cells on the drawing aren't side-adjacent but they still block Limak from passing through. Similarly, if Limak was allowed to move to any of 8 corner/side-adjacent cells, black cells would have to touch by sides to block Limak from passing through.
The idea of a solution is to find CC's (connected components) of blocked cells before reading queries, and then for every query see what CC's are connected with each other by temporarily blocked cells. To make our life easier, let's treat the blue sides as blocked cells too by expanding the grid by 1 in every direction. Then for every query, we want to check if new blocked cells connect the bottom-left CC and top-right CC.
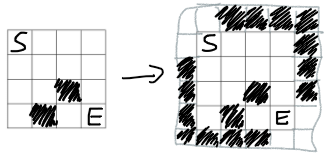
Before reading queries, we can find CC's of blocked cells (remember that a cell has 8 adjacent cells now!). Let's name those initial CC's as regions. When a temporarily blocked cell appears, we iterate through the adjacent cells and if some of them belong to initial regions, we apply find&union to mark some regions as connected to each other (and connected to this new cell that is a temporary region of size 1). This can be done in 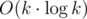 where k is the number of temporarily blocked cells. This solves the easier version of a problem, where we just check if Limak can get from one corner to the other — if the two special regions are connected at the end then the answer is "NO", and it's "YES" otherwise.
where k is the number of temporarily blocked cells. This solves the easier version of a problem, where we just check if Limak can get from one corner to the other — if the two special regions are connected at the end then the answer is "NO", and it's "YES" otherwise.
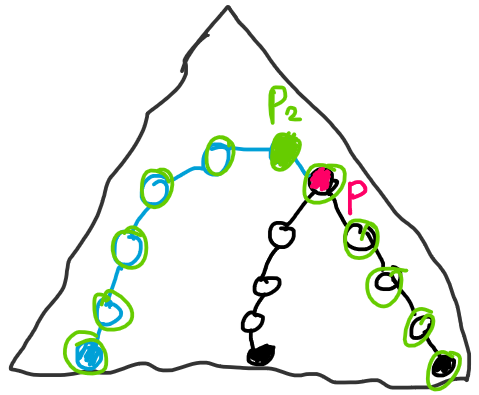
What about the full problem? Limak wants to move to the opposite corner and back, not using the same cell twice. If you treat a grid as a graph, this means checking if there is a cycle passing through the two corners (a cycle without repeated vertices). It's reasonable to then think about bridges and articulation points. An articulation point here would be such a cell that making it blocked would disconnect the two corners from each other — it's a cell that Limak must go through on both parts of his journey. Our dual problem becomes: check if the two sides are almost connected i.e. it's enough to add one more blocked cell to make the connection (that cell must be an articulation point). The previously described solution needs some modification.
We did F&U on regions adjacent to temporarily blocked cells. If some region was connected with some other region in the current query, let's call it an interesting region — there are O(k) of them. If we preprocess the set of pairs of regions that are initially almost connected (it's enough to add one more blocked cell to make them connected), we can then for a query iterate over pairs: a region connected to the bottom-right side and a region connected to the other side, and check if this pair is in the set of almost-connected regions. There are O(k2) pairs and if any of them is almost-connected, we have an almost-connection between the two sides and we print "NO", because Limak can't avoid revisiting cells.
My code: 50164800.



 . What should be stored in such a tree?
. What should be stored in such a tree?
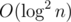 . The limit from the statement is
. The limit from the statement is 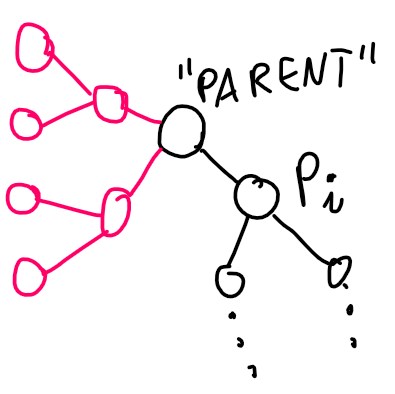








It is deleted
Yes it can be, it says so in statement, and you can look at worse rating to confirm :)
thanks, I just reread the statement :'( and worse has no rating :v
I think, you mean worse.
I think, you mean worse
Oh Coach Ray
could you please attach this tutorial to the contest materials? I haven't found it till now! thanks.
Didn't get the last part "solution" of editorial of E-problem. If someone can explain it again with an example it would be great :)
Consider the regular expression
.*2.*0.*1.*7.*and build its automaton:It's evident that if the requested (sub)string matches this expression, then it contains the "2017" subsequence. Now we are to delete some letters from it to exclude the "2016" sequence.
Weigh the automaton transitions:
W(0 -> 0 with '2') = 1,W(1 -> 1 with '0') = 1, etc — to stay in the current state when receiving a letter which moves us to the next one, we should delete this letter. Also,W(3 -> 3 with '6') = 1andW(4 -> 4 with '6') = 1— if we've already taken "201" or "2017", we must drop every '6' we encounter. Other edges not mentioned above have weight of 0.Define a 5x5 matrix
mfor a strings, such thatm[i][j](i <= j) is a minimal cost to get from stateito statej, feeding the automaton withs's characters.Suppose we have two strings,
pandq, and their matrices,mpandmq. We can easily merge them, obtaining a matrix for their concatenation (looks similiar to Floyd's algorithm).Notice that matrix merging operation is associative. So, we can build the RMQ on it.
When using segment tree, we gain
O(n*log n + q*log n)time andO(n)space solution, online.23454158
It could be improved up toO(n + q)using RMQ to LCA conversion and someO(n)/O(1)(precalc/query) LCA algo (e.g., Schieber-Vishkin).thanks :)
Hey , I have a doubt , have a look http://pastebin.com/TwgNC70X
For "1", the matrix should look like:
For "6":
And for "16":
I implemented the idea as per your explanation, but getting TLE. 23502332. Any suggestions?
It seems that you store too much data at a single node of the segment tree. There are only 14 numbers need to be take care of. (Pay attention to the constraint j>=i)
15, actually. However, it is possible to get AC even without this optimization.
Seems that you allocated too few nodes.
1 << 19 < 4 * 2e5.I guess number of nodes in segment tree is at most 2^(ceil(log2(n))+1) = 2^19. Please correct me here.
Oh, you are right! Always thought that the upper bound is
4 * n. Thank you!There are plenty of ways to optimize your code.
std::arrayor just plain arrays wrapped with astruct) will prevent your program from using dynamic memory. Heap manager would be just happy.cin.tie(nullptr);at the beginning ofmainto prevent from flushing stdout whenever you read something.I suppose using any of these (probably, except the last one) should be enough to get AC. Applying all these techniques together, I managed to get AC in less than 400 ms: 23491398.
Thanks, got AC with applying 1 and 2. 23512670. Also, it was the first time, I heard of non-recursive segtree. Thanks for that too!
Nice solution! Help me a lot! Thank you very much!
Finally, after reading it 3-4 times I got your point. Will implement it today! Thanks SirNickolas. Can you suggest some more problem that require building such automation?
If we have just some string s, then how can we find min chars to remove that s contains "2017" as subsequence and does not contains "2016" as subsequence using this automation? And how to connect it with dp?
Can C be solved using Binary search ? If YES , then how ?
Yes
Binary search over the rating before first round
Check if it's possible to have that rating without problems/conflicts in divisions at the start of all contests
if no problems try bigger numbers
if there are problems like:
1: rating is < 1900 and we are supposed to be in div1 in current contest: try bigger numbers
2: rating is > 1899 and we are supposed to be in div2 in current contest: try smaller numbers
The answer is infinity if all contests are in div1
Solution Link
The tricky thing here is the upper limit on t-s.
Since the firework cannot fly further that |kt| from the startpoint after k iterations, you'll find yourself in the (2nt)^2 square that is equal to 300 * 300.
Hence O(n * 2^n) turns to O(n^3 * t^2)
I tried to implement his solution. It's giving me the right output of course but I am getting TLE on higher recursion levels since as you have pointed out, it's exponential(at least my code). Can someone help me out?
There can be at-most
2^29particles afterNexplosions. If you consider a state of the particle in terms of Grid,Level,Direction(X,Y,T,Dir)fromPigeon Hole Principlethere must exist (at some point2^k > 321^2 * 30 * 3^2) two or more particles starting in the same Grid, moving in the same direction at the Same level. For these kinds of particles,you only need to track one instanceof it. By this way you wont be keeping track of more than321^2 * 8particles at an instance.This leaves you with a complexity of
O(Height*Breadth*Levels*Distance*Directions)O(N^2 * 30 * 5 * 8)O(N^2)In a way, I had a very similar solution to the intended solution for E. Instead of a segment tree storing a 5*5 matrix, I implemented a sparse table to the same effect (23455422). As a result, the memory limit acted and I had to make a last-minute compression to take out the cases where
i>j. I wonder if the memory limit was imposed to prevent the sparse table solution.I can't figure out what's wrong with my submission for C : 23443890
Where is the mistake in the code ?
lower must be -inf
Thanks a lot. My bad — I thought ratings couldn't be negative. Figures. If ya think ratings are low now — they can always go lower. Reminds me to read the question properly and never take anything for granted.
Still can't understand E.. How by removing digits we can get longer segment? (about T[i][j]).
I understood it as while merging segments, T[i][j]= min(left.T[i][k]+right.T[k][j]); So T[i][j] for some segment represents the minimum chars to be deleted to produce substring i+1..j of 2017. This also means that the 0..i part of 2017 will be taken from the left of this segment.
Look at my submission to see the assignment of matrix for leaf nodes. Lets say we encounter a 0, then mat(1)(2) becomes 0 as if we are taking 2 from left side, then this segment can provide 0 to complete 20. If we skip this 0, then it allows 2 to be taken from left side of this segment, and to skip 0, mat(1)(1)= 1. It wasnt very clear to me in beginning how its working but give it some time and then it would be clear.
For segment "7" you have T[3][3] = 0. Why not 1? If you've already got "201" and encounter '7' you have to remove this '7' to stay in the state 3, don't you?
Perfect example would be something like 20110667.Here optimal solution is to remove the zero at second place.For the segment(20) in the tree t[0][1]=1(we will have to delete 0).Although t[0][2]=0 but when it propogates upwards it is not optimal because we will either have to delete 2 1's or 2 6's
thanks!
In problem E, I stored another kind of information in the segment tree.
Suppose we have some string s1 ("2017", for example) and some other string s2 ("2016", for example). We want our current segment to contain s1 as a subsequence and do not contain s2 as a subsequence. What is the minimum number of deletion we have to make?
This information could be updated using the answers of the node's children in the segment tree.
For example, let s1 = "2017", s2 = "2016".
Then we have to consider the following values:
AnswerOfTheLeftChild("", "2") + AsnwerOfTheRightChild("2017", "2016")
AnswerOfTheLeftChild("2", "20") + AsnwerOfTheRightChild("017", "016")
AnswerOfTheLeftChild("20", "201") + AsnwerOfTheRightChild("17", "16")
AnswerOfTheLeftChild("201", "2016") + AsnwerOfTheRightChild("7", "6")
AnswerOfTheLeftChild("2017", "2016") + AsnwerOfTheRightChild("", "6")
I generated all of such pairs (s1,s2) ad figured out, that there are only 14 of them. So it is possible to store 14 values in the segment tree node.
I managed to solve problem C with a different approach.
Keep two variables:
fromdenoting the smallest possible value for the rating, andtodenoting the highest possible value for the rating.if at some point you were in a div2 contest and your smallest possible rating is larger than 1899 print Impossible, or if you were in a div1 contest and your highest possible value is less than 1900 print impossible.
Otherwise, if you are at a div2 contest then
to = min(to, 1899), or if you are at a div1 contest thenfrom = max(from, 1900), then increase (or decrease) both variables by the amount of points you earned at the current contest. If at some pointfromwas higher thantoprint Impossible.At the end, the rating is equal to the highest possible value which is
to.Unfortunately, during the contest I was hacked because I forgot that the initial rating can be negative :(
Accepted Code
You just explained how to solve inequalities from the editorial.
I have an alternative solution for problem C. For the most part of the contest, I simply missed the simple solution.
Here's what I did instead.
Thread separately the cases when I have only one type of divisions (either div1 or div2). (Actually, solving the case when I have only div2 contests should have given me a huge hint for the simple solution earlier in the contest, but I had a bug in my logics).
Now, there will be at least one contest when I'll change my division (from div2 to div1 and vice-versa). Let's take the first one and suppose I changed from div1 to div2 (the other case is identical). Then, rating[i — 1] + change[i — 1] = rating[i].
But rating[i] <= 1899, so rating[i — 1] + change[i — 1] <= 1899. So rating[i — 1] <= 1899 — change[i — 1]. (change[i — 1] is negative, since I fall in div2, so no problem here). rating[i — 1] will be between 1900 and 1899 + abs(change[i — 1]).
But abs(change[i — 1]) <= 100, so actually rating[i — 1] can take maximum 100 values. After I know that rating[i — 1] has a certain value, everything else is uniquely determined, so I can just simulate the values.
This gives me a O(max(changes) * n) solution. The implementation is pretty painful, but this is the price I payed for missing the simple solution: 23459419. Lesson learned, next time spend more time thinking for something simpler, it will pay off :) Good to know bicsi still loves me despite my newbie performances. <3 <3 <3
An alternative solution for D:
We again use the observation that only cells within 150 can be coloured so there are at most 300*300 cells to keep track of.
Suppose we are finding which squares are coloured by some firework of depth k, and we already know which squares are coloured by everything in the right 'subtree' (note there are at most 300*300). Then to get which squares are coloured by the left subtree, we can simply reflect them about the line formed by the the current firework.
Thus we can colour any single path in the 'firework tree' (for example we could just dfs, recursing on only the right subtree every time) and then reflect the tree as we go back up.
Then, the complexity, where S is the grid size, is O(S^2 * depth).
A last detail is how do we do the reflection? There are only 4 types of flips depending on which way the current firework is going: up/down, left/right and the two diagonals. So we can just do some slight case bashing with the coordinates...
Code: http://codeforces.net/contest/750/submission/23437226
I stucked and tried to solve third problem C "New Year and Rating" in the competetion. However, I couldn't solve. My codes reach 100 lines, but when I look the top-tier programmer from Final Standings, they solved about 10-15 line of code. It is clear that I have a trouble in way of thinking.
So, I wanna ask, why I couldn't? Do I need to work some algorithm design topics or just is it about experience?
This one's quite ad-hoc to be honest. With this problem, you should go by the concept of intersecting ranges, which are determined by the inequalities x <= 1899-c[i] or x >= 1900-c[i]. If you go by that concept, your code should be very short like the top tier guys. Not to toot my own horn, but my code for this problem was also around 10-15 lines ;).
Most of this ability to think of simpler solutions comes from experience and practice. The more problems you've done, the more likely you will have seen the techniques used in a contest problem.
I felt the same after the contest.
I wanted to ask about it in a blog post, but I think this is a good place.
Does anyone know any similar problem that is solved with min / max?
this
Can someone explain me this testcase of problem B(New Year and North Pole). 1 80000 South. Answer for this case is NO. But as for me we start at North Pole, go south 40k,implying we are at North Pole,again go south 40k, we end up at North pole Right.
Thank you.
"If at any moment of time (before any of the instructions or while performing one of them) Limak is on the South Pole, he can move only to the North." So after having completed 20000 km of journey, Limak is now at South Pole, but from South Pole you can only go North, but the instruction had said about going South, thus the description is no longer valid. So answer will be NO.
The important thing which many of us missed is to also check the validity of the instructions.
Hi, Please anyone help .. My submission on Problem E is getting Runtime Error.. here is my code
The array size for segtree.
yeah.. I got it.. thanks
very good style of editorial
Can someone explain the problem G? It is not clear. Thanks in advance.
http://codeforces.net/contest/750/submission/23469026
Can someone please spend some time and help point out where did I made a mistake? I think I should've blocked all causes of Idleness TLE but it doesn't.
Can somebody explain me the concept of duality? Or at least what I need to know about it for solving H? I know about duality and the dual plan from the voronoi diagram but I don't see any correlation. Thank you in advance!
So... what's the complexity of solution in G problem? I've accepted O(log6), but I had some hard times trying to optimize it. My dynamic part works O(log4) and I'm not sure how to do it faster :'(
O(log5): fix the sum of popcounts of a and b rather than fixing each popcount separately and then do dp bit by bit, keeping track of current sum of popcounts and making sure a+b is equal to something.
I suspect it can be done in O(log4) if we don't fix the popcount sum but I'm not able to work out the details.
"It turns out that lengths of sides are enough to compute exact value of LCA. Find a formula on paper or see my code (the top of this page)"
Can anyone provide me a paper write about that or give me a hints to prove its correctness. It is still not clear to me.
Many thanks.
Same, need help here :(
Let's fix lengths of sides (la and lb), and let's denote LCA by v.
Then, s = av + b, where a depends only on la and lb. b depends on actual nodes chosen but you can see that 0 ≤ b < a always.
From discrete mathematics (or common sense) we know that given m > 0, every number x has unique representation x = pm + q such that 0 ≤ q < m.
Therefore, there is only one possible set of values for v and b: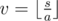 and b = s - av.
and b = s - av.
Errichto, can you please point some problems that inspired problem E's solution? Thanks in advance! (It would be very useful if problem authors could point some similar problems to those they just made for the round. There are some pretty cool recurrent-but-not-so-famous techniques that just won't stop showing up!)
+1 to you. While looking upon solutions, almost everybody who solved it had a similar approach. They have come across this before.
Some similar problem please ?
http://codeforces.net/group/BDIXyZZHhT/contest/205914/problem/F
The solution for this problem has a similar merge function (not sure if there's another solution). The limits allow SQRT-Decomposition to pass. There are only update queries, but the same idea solves the range query version.
Do you know "calculate n-th (n ≤ 1018) Fibbonacci number" problem?
Yes, with fast exponentiation. Solutions for problem E use fast exponentiation?? (I still haven't had time check the solutions, but this is a surprise to me, because I have solved some tough matrix exponentiation problems and this idea didn't show up to me during the contest... Actually, the idea of using matrices didn't cross my mind in the first place)
Well, here you have not exponentiation but "product on the range [l;r]" (and with wierd multiplication)
And I call this thing multiplication, because it is similar in many aspects (what is important it is associative, but you may also "multiply" block matrix or "multiply by vector" etc)
This great post gave me the key idea to solving problem E. See also this article, which dives deeper and focuses on the implementation.
They also have Russian translations (well, the second one was originally written in Russian and then translated into English). Don't miss this nice article (Russian only, sorry).
Ok, I've just solved problem E and realized the real point of the exercise. The recurrent technique you should be familiar with is not only segment trees and monoids (the algebraic structures over which segment trees are built upon). You should also be familiar (at competitive programming level!) with DFAs/NFAs and their monoid behavior when represented by matrices. What I mean with "familiar at competitive programming level" is that you should be capable of adapting the representation/monoid to solve the problem (the solution is not a straightforward application of the technique).
Thanks to SirNickolas, the best reference: http://jkff.info/articles/ire/
My solution: 23493355
Hello! I don't know how this code got AC, but there is one mistake in your code. In the automaton initialization "memset(m,oo,sizeof m);" is incorrect, since this function aims to perform "byte-wise" initialization and therefore all cells in this array wouldn't be oo as expected.
However, I'd be very grateful for your code because the segment tree and the automaton parts are very very simple, clean, pretty and easy to understand!!!! Thank you very much!!!
thank you, friend from the future! maybe $$$oo = 0x3f3f3f3f$$$ could work?
I don't know. You can give it a try!
it works ¯\_(ツ)_/¯
https://codeforces.net/contest/750/submission/107116819
these kind of editorials are the best step by step hints rather than full blown solution.
i encourage codeforces to adopt spoilers inside the editorial
Can someone explain how we can get these convertions in D ?:
Set up two arrays of changes in y-coordinate and x-coordinate of the eight directions like this:
dy[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, dx[8] = {0, 1, 1, 1, 0, -1, -1, -1} where -1 refers to North/West and 1 refers to South/East. So dy[0] and dx[0] means the fireworks moves towards North (0 degree), dy[1] and dx[1] means the fireworks moves towards North-East (45 degrees), etc.
When the fireworks splits, two new fireworks of +45 degrees and -45 degrees are formed, so you can get the new directions by moving your pointer to adjacent elements.
(dir+1) % 8 should be quite easy to understand (turning 45 degrees clockwise), but for anticlockwise turns we add 7 because (dir+7) = (dir+8-1).
Thanks a lot!
Can someone explain how to do G in O(log(s)^4). I could only come up with a O(log(s)^5) solution as described here.
What does it mean in F editorial? Can't get this part for hours >_<
You know that that max distance of the root from the LCA is atmost 3.
Go to the last unvisited neighbour of the LCA. Let it be v1 (v1 is at distance 1 from LCA). v1 has two unvisited neighbours. Let them be v2 and v3 (both are at distance 2 from LCA). Now, each of v2 and v3 have atmost two unvisited neighbours each. Let them be v4, v5, v6 and v7 (first two are connected to v2 and last two are connected to v3). All four of these v4, v5, v6 and v7 are at distance 3 from the LCA. The root is guaranteed to be one of these (from v4, v5, v6 or v7).
If you can't understand the above explanation, drawing a diagram might help. :)
Thanks, got that
Looking forward to a more detailed solution for problem H, or any materials about duality in this problem?
This duality is min cut max flow (you can see this problem for a similar idea: https://code.google.com/codejam/contest/3014486/dashboard#s=p2 ).
We want to know "is there a flow between the top left corner and bottom right corner with value at least 2?". Here, we have a grid graph, and we can only move in 4 directions. We can take the dual to convert it to "is there a cut with cost at least 2?". This is equivalent to finding "is there a cut with cost at most 1?" and negating the answer.
What is a cut of the grid graph? It turns out it is an 8-connected path from the bottom or left side to the top or right side (excluding the top-left corner and bottom-right corner).
Here, grid cells that are blocked cost 0, and grid cells that are empty cost 1, and we want to know if a path exists with cost at most 1.
Really helpful, thank you!
So in problem B, we can go west and east any number of kilometers, but we are not allowed to go 20,001 KM to the South for example ?
In other words, in this case
3 1 South 1000000000 East 1 North
I am allowed to go 1000000000 KM to the East.
But in this case,
1 40,000 South
I am not allowed to move around the earth :D logic xD
You mean incorect and worse
Are you talking about something in an editorial?
Hi guys, I have written code for this part <Let's first use the Algo to answer simpler queries: "for the given segment check if it's nice">.
Here is the code
http://ideone.com/gvpKLk
The node can be compressed to pre6[5] and pre7[5] where preX[i] holds the next state after reading the characters of the segment given that i prefix characters have already been read.
http://codeforces.net/contest/750/submission/26921295
It is code for A. It's very easy. Time- 240 minutes to midnight. We must deduct k from 240. Then we only deduct time on a task and add to nasa 1. Cout ans;
(Code for C++)
У кого есть другие варианты?
http://codeforces.net/contest/750/submission/23482626 Shorter )
lots of define)))
It's pattern which I didn't write every time, but it helps very well (and it's my old code, now pattern is biiger :D). Compare my and your int main() content.
I can't watch author's codes
At problem D. If a firework hits Limak,he dies?
Cannot view setters codes.
I can not see the setters code.
I am not able to see 24067296. It shows I am not allowed to see this page. Plz help me out..
Me neither.Dont't worry, but it may be a system bug.(Or something else I don't know)