→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
46:50:19
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
46:50:19
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 21.11.2024 18:44:43 (h2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Даже Флеш завидует скорости, с которой опубликовали разбор.
Kак можно полностью увидеть тест/претест к задаче?
В ваших посылках кликаете на номер нужной посылки, листаете вниз и там есть все тесты с ответами.
А если часть теста обрезана? Если тест слишком большой
Тогда вам уже ничего не поможет
The most brilliant solution to problem D must be the one with max-flow min-cut theorem in my opinion :)
oh, I think about using maxflow here. But I think it is hard to make network here. Moreover complexity of such solution would not pass in TL, am I right?
I think so!
well, in my opinion, just simple observation was required.
Since, we are given that frogs can jump on the distance of "L" , we can maintain the window of the size "L", and for this window, we can find the sum, wherever the sum is minimum , that is our answer. Because it will become bottleneck for all frogs. :) .
http://codeforces.net/contest/965/submission/37608075
This is link to my on contest solution. It took me less than 10 minutes to solve this D. it was way too much easier than normal D.
lol your solution is max-flow min-cut theorem.
hmmm, sorry about that. I don't know much algorithms. I don't know what I have implemented is maxflow or something else.
I just implemented with my intuition. I will look into Maxflow algo.
It's not the max-flow algorithm, it's just the idea of max-flow min-cut theorem. In your solution, you are using the fact that "max-flow is min-cut", where min-cut is the min(sum) of a length L. ;-)
Nice solution!
your remark only justifies that your output must be greater or equal to the real answer, since real answer cannot be greater than the bottleneck; but you give no proof that your output "IS" the real answer. Though, with some careful thought, you can actually prove this, or more specifically, you can easily construct a solution /scheme where the frogs with the same num of bottleneck can jump across the bank
A pretty late reply keeping in mind the contest happened 2 years ago, but I used a very similar logic, instead I maintained a dp, where dp[i] gives the max frogs ith place can hold which allows them to reach the riverbank, and then calculated minimum sliding window sum of length L over that dp.
I got an accepted verdict but clearly our logic is different (Feel free to correct me if I am wrong). Any thoughts on why this is working out?
AC submission:
https://codeforces.net/contest/965/submission/91799129
D can be solved with O(n) compexity. Imagine a graph where it is n * 2 vetices. From source you have edges to 1, 3 .. 2 * k — 1 vetices with capacity INF. From i'th vertice if i is odd you have edge to i + 1 vertice with capacity a[i]. From i'th vertice if i is even you have edges to i + 1, i + 3, i + 2 * k — 1 with capacity INF. if i is even and i / 2 >= n — k you have edge to sink (smth like that i can make little mistakes) And you can instead of building such a big graph and running max flow algorithm just try to find minimum cut. And after some greedy thoughts it is clear that you must choose segment [i, i + k — 1] with minimum sum of a[j] where j belongs to [i, i + k — 1]. It can be done with just a pair of loops in your code. See my implementation for details.
http://codeforces.net/contest/965/submission/37610259
Another (maybe easier) proof is that, if you imagine you know the solution with the maximum number of frogs and simulate the process for sequentially with all the frogs, making sure that the left-est frog moves at all times, you can see that every time in this process the frogs will be in a contiguous segment of length at most l. So the solution should be at most the minimum sum over all l-length segments. Once we found this upper bound, proving that it is the answer is straightforward.
hello there,can you please tell me why must i choose continue segment? what if i Don't choose one of the continue edge? i think that this maybe a minimal cut ,too
when you take i'th vertice to first set ( by cut ) if i is even you need to take next k vertices with odd i to first set (otherwise you'll add INF edges to your cut) therefore it is clear that it must be k consecutive odd vertices which goes in first set when his connected even vertices goes in second set. And as it must be k consecutive a[i] you can just not add other a[i] to your cut.
I solved problem using fenwick tree, greedy approach. But I dont understand your solution. Why it is important if i is even or odd? How can that be important?
Can someone explain why my solution passed tests. I want to believe that complexity is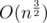 but i can't proove it.
but i can't proove it.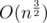 states in dp because it is a trie. But there is also transitions and i've stuck here how to estimate number of transitions?
states in dp because it is a trie. But there is also transitions and i've stuck here how to estimate number of transitions?
Shortly it is dynamic programming on tries. dpv, x = minsum. Where v is number of vertice in tries. x — number of words that we didn't written in final set of prefix (it means that we will write it higher in tries — with smaller prefix).
There I do stupid smth like knapsack on a tree. dpv, x = min(dpv, x, dpto, y + dpprevz for all y, z witch satisfies condition y + z == x. It is usual knapsack on a tree.
So it should work in O(n2). But i added condition dp[v].size() = min(depth, cnt[v]) where cnt[v] — number of terminal vertices in subtree. And it gives
This is implementation http://codeforces.net/contest/965/submission/37615468.
Can i solve problem div. 2 C using bisection method?
Is this logic correct?
For C, Bonus 1:
Same logic as given.
Just one change: to find xMax formula used earlier was: n / ( k * (i — 1) + 1 ), where i is the current D (in a for loop of D). (I did + 1 at-last to include Arkady as leftover use was not allowed). It should be less or equal to M.
Here, we just have to first check:
if(n % (k * (i — 1)) != 0) then Arkady will get leftover in last level and (n / (k * (i — 1)) in other levels. (Need to handle a case when value of n / (k * (i — 1)) exceeds M as it will be added to leftover and so on...)
else same as earlier.
If this is correct then can anybody tell me how to make it work for large values of D? (1 <= D <= n)
I don't think that works.
36 2 9 3
when d = 1 or 2 : impossible
when d = 3 : possible distributions = 6,7,8 , formula gives 6. best is 7.
For E, I had right idea but failed in implementing minimizing depth.
There is a much simpler, two pointer solution to D. Probably similar to the one bicsi gave.
The idea is to maintain a 0...w array 'reach' where reach[i] tells us the number of frogs that have reached the i'th unit at the i'th step. Note that reach[i] can't be greater than a[i], because we can't accommodate more frogs than the number of stones. We start by having infinite number of frogs having reached the 0th unit. For any i <= l, reach[i] = a[i]. This is because the frogs from 0th unit can directly jump till here.
The key insight here is that for any i > l, we should start letting the leftmost frogs who can reach i, jump till i. I.e first all frogs from the (i — l)th unit jump till i, then (i — (l-1))th and so on. We do this till either i'th unit's capacity is reached, or we've run out of frogs. You can use a pointer 'j' to track where the leftmost frogs are. Just make sure that j >= i — l. Answer is reach[n].
http://codeforces.net/contest/965/submission/37625008
Thanks. I found this easier to understand than the editorial.
I don't get why in C one doesn't need to compute min x for the iterated d like in the editorial. Computation of max x always works, but for me it seems that sometimes max x could make us take candies more than d times for the first person. Why is it never the case?
what's more confusing is that if for some
d, ifmax(x) > Mthen takingx = Mwill always be valid for thisd!!! I really cannot account for this.37640931(should fail!)
37648582(probably correct)
Hi! What is "smaller-to-larger optimization"? Does someone has a link to read about it?
Thanks
According to the code(http://codeforces.net/contest/965/submission/37617599), It just merge two sets by joining smaller one to larger one.
I believe this idea is commonly known as 'DSU on tree', you can read more about it here
Thanks! I'm going to read about it
Does a binary search solution works for C ?
how can i solve C's bonus 2 part?
Anyone else solved D with BIT?
i did http://codeforces.net/contest/965/submission/37911989
can someone please explain E!
Firstly,we build a trie tree for all names.Now,the total length of these original names is the total depth of all names.
As we go from the bottom to the top of the trie tree,if a node doesn't contain a name, it is obviously to place the name which is deepest(longest name) to current node,this case is optimal.
And after we go to the top of the trie, the ans will be the total depth of the trie
Haha, this problem is also solvable via DP. Let dp[i] — the max number of frogs that can get up to distance i. We calculate dp[i] based on values of dp[i — l]...dp[i — 1], only we delete dp[i] frogs from the dp array starting from index i — l, not to count duplicate frogs. This TLs on test #16, so I simply keep track of the current sum dp[i — l]...dp[i — 1] in a variable, which runs in ~200 ms.
Code: https://codeforces.net/contest/965/submission/46261137
Editorial to https://codeforces.net/contest/965/problem/C is one of the most arrogant ones I ever did read on codeforces.
Wow, so many solutions to problem D. Here is yet another one :P
I do a DP on a greedy. I break the entire $$$w$$$ length into $$$w/l$$$ segments of length $$$l$$$ each. And for each segment, I try to fill up this segment in the rightmost way, greedily. This can be done by DP.
88428808