Всем привет, сегодня я расскажу решения часто встречающихся задач на подсчет количества элементов, меньших k, и разные способы их решения. Перед прочтением рекомендую ознакомится с предыдущим постом, в котором были разобраны некоторые подзадачи.
Задача 1. Подсчитать количество элементов, меньших k на всём массиве с возможностью добавления и удаления элемента.
Решение в онлайн: простым способом является написание ДД по ключу, в котором нужно просто подсчитывать размер поддерева.
Сложность:  на любой запрос, но средняя константа за счёт ДД.
на любой запрос, но средняя константа за счёт ДД.
Решение в оффлайн: Прочитаем все запросы и запомним все значения и отсортируем их. Построим Фенвика, изначально заполненного нулями. Если появляется запрос на добавление, то добавляем 1 в позицию с этим элементом; удаление — отнимем; количество элементов, меньших k — сумма на префиксе.
Сложность:  с очень маленькой константой. В целом, пишется быстрее и короче чем ДД. Аналогично можно решать множество дальнейших задач в оффлайн и уменьшать константу.
с очень маленькой константой. В целом, пишется быстрее и короче чем ДД. Аналогично можно решать множество дальнейших задач в оффлайн и уменьшать константу.
Спасибо Kaban-5 за идею.
Задача 2. Подсчитать для каждого элемента массива количество элементов, не больших него самого на префиксе в оффлайн.
Давайте отсортируем все элементы по паре <a[i], i>. Пусть у нас есть Дерево Фенвика (или дерево отрезков) на n элементов, изначально заполненное нулями. Теперь будем по отсортированному порядку ставить 1 в текущую позицию и считать сумму на префиксе — это и будет количество элементов, меньших текущего значения.
Сложность:  с очень маленькой константой.
с очень маленькой константой.
Спасибо Holidin за интересную идею.
Задача 3. Усложним предыдущую задачу: будем отвечать на запросы вида количество элементов, меньших K на отрезке [L; R].
Решение в оффлайн: будем действовать аналогично предыдущей задаче. Заведем Дерево Фенвика на n элементов, заполненное нулями. Пусть у нас есть 2 типа событий: 1) написать 1 в некоторую позицию, 2) посчитать кол-во элементов, не больше K на отрезке [L; R]. Тогда отсортируем события по значению(a[i] или k соответственно), а потом по позиции(i или +INF соответственно: если событие второго типа, то важно, чтобы оно выполнилось после событий первого типа). Итак, теперь ответим на все запросы. Пройдемся по отсортированным событиям и если оно первого типа, то поставим 1 в нужную позицию, а если второго, то посчитаем сумму на отрезке [L; R] нашим Фенвиком.
Сложность: Пусть N = n + q, тогда асимптотика 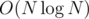 с опять же очень маленькой константой за счёт Фенвика.
с опять же очень маленькой константой за счёт Фенвика.
Решение в онлайн: отсортируем массив и построим MergeSortTree по индексам в отсортированном массиве. Пусть нам пришел запрос посчитать количество элементов, меньших K на отрезке [L; R]. Это эквивалентно подсчету количества индексов в отосртированном массиве на префиксе до элемента pos, у которых индексы находятся в [L; R] (pos — индекс первого элемента, большего K в отсортированном массиве). Двоичными спусками найдем эту границу pos, параллельно считая ответ в поддереве — это будет разность lower_bound'ов по r и l в левом поддереве, если мы переходим в правое. Теперь применим технику fractional cascading.
Получили сложность  на запрос.
на запрос.
Задача 4. Нужно уметь выполнять операции 2 типов:
- Посчитать количество элементов, меньших K на отрезке [L; R]
- Изменять любой элемент массива
Построим дерево отрезков, в вершине которого будем хранить ДД по ключу с возможностью подсчета количества элементов, меньших K(ровно так же как в 1 задаче). Тогда отвечать на запросы обоих типов становится очень просто, и это сделает любой человек, который хоть раз писал ДО с суммой на отрезке и обновлением в точке.
Сложность: 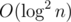 на запрос с приличной константой.
на запрос с приличной константой.
Задача 5. Давайте ещё больше усложним задачу 3. Теперь есть 3 типа запросов:
1. Удалить элемент на позиции pos
2. Добавить элемент на позицию pos
3. Посчитать количество элементов, меньших X на отрезке [L; R]
Решение в онлайн: Давайте применим магию корневой декомпозиции. Разобьем массив на блоки по корню и в каждом блоке будем дополнительно хранить ДД по ключу для подсчетка количества элементов, меньших X.
Сложность:  на запрос.
на запрос.
Я просто оставлю это здесь(здесь тонна оптимизаций, но всё равно при n, q <= 1e+5 не проходит на серверах яндекса):
Спасибо SerezhaE, который помог оптимально подобрать размер блока и заменить ДД на обычный vector таким образом, что асимптотика стала  с небольшой константой. Его решение описанно в комментариях, а код я оставлю тут. Кстати, задачка зашла.
с небольшой константой. Его решение описанно в комментариях, а код я оставлю тут. Кстати, задачка зашла.
Решение в оффлайн:
Получим относительный порядок элементов, с помощью ДД по неявному ключу(из предыдущего поста). А затем воспользуемся задачей 4.
Сложность: Получение относительного порядка  и далее
и далее 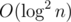 далее для каждого запроса.
далее для каждого запроса.
Я таки превозмог себя и написал это, но все еще ТЛ, да еще и памяти стало жрать как конина. Проходит тестов больше чем корневухой. Если вы подскажете мне, как это можно улучшить, буду рад.
Задачи 1 и 2: ACMP №112 ACMP №647 ACMP №441
Задача 4: Задача на spoj на сумму различных элементов
Задача 3 в чистом виде мне ещё не попадалась, а задачу 5 на русскоязычных сайтах я не нашел, она была у меня в ЛОШ.










