Всем привет, мне так понравилось как растет мой вклад я вижу, что вам понравился разбор в предыдущем посте, поэтому я решил периодически рассказывать о разных задачах, во многом, с применением не очень сложных структур данных.
Сегодня я рассажу вам об оптимизациях дерева отрезков и декартовых деревьях(все вещи аналогичны ДО), позволяющих скинуть лишний логарифм в асимптотике, также разберу одну подзадачу, позволяющую решать кучу задач.
Будут разобраны:
1. Двоичный спуск
2. Fractional cascading
3. Задачи с удалением и добавлением элементов
1) Двоичный спуск
Пусть вам надо найти элемент, начиная с которого сумма больше K, а вы очень упорный и не любите частичные суммы, зато хлебом вас не корми, дай дерево отрезков написать! А всё это надо сделать за log!! Как быть? На помощь приходят двоичные спуски!
Пусть вы знаете сумму в левом поддереве, тогда если она больше K0, то переходим в него, иначе — в правое поддерево с K1 = K0 — sum(left).
В целом, двоичные спуски требуются, если в какой-то задачке вы хотите бинпоиском узнавать что-то через ДО: аналогичной идеей вы каждый раз понимаете в какое поддерево нужно спуститься.
Сложность: 
2) Fractional cascading
К сожалению, на русскоязычных ресурсах об этом ничего нет(UPD: на e-maxx, говорят, есть), хотя это моя сама любимая оптимизация, которая мне ни разу не пригодилась, но делает крутые вещи :)
Итак, задача: найти k-тый элемент на отрезке [L; R], если бы отрезок был отсортирован — это назывется k-тая статистика на отрезке. (Бонус: придумайте как решать эту задачу персистентным ДО)
Ну а в задаче такие ограничения, что требуется 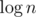 на запрос.
на запрос.
Для начала дадим понятие MergeSortTree — это дерево отрезков, в вершине которого хранится отсортированный массив из 2-х отсортированных массивов его сыновей. Интересно, почему же такое название у этой структуры?
Итак, придумаем решение за 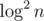 на запрос. Давайте отсортируем массив по значениям, и построим MergeSortTree по индексам этого массива. Для примера вот картинка:
на запрос. Давайте отсортируем массив по значениям, и построим MergeSortTree по индексам этого массива. Для примера вот картинка:

Поймем, сколько элементов из [L; R] в поддереве, за которое отвечает данная вершина в дереве отрезков. На самом деле это очень просто посчитать: давайте возьмем lower_bound по L и R и найдем разность между ними — это и будет наше количество элементов. А теперь двоичными спусками будем находить k-тый элемент с помощью предыдущего утверждения. Заметим, что массив у нас отсортирован, поэтому мы получим именно k-тый элемент.
А теперь то, зачем мы все здесь собрались, расскажу о fractional cascading. Давайте помимо отсортированных массивов в вершине хранить еще два: l и r, такие что l[i] означает количество элементов в левом поддереве, которые не больше a[i], аналогично c r. По сути эти массивы означают upper_bound. Аналогично можно завеcти и lower_bound.
Картинкой построение upper_bound:

Вернёмся к задаче и поймем, что теперь вместо бинпоиска в сыновьях мы можем просто перейти по этим индексам L и R и найдем опять наш отрезок [L1; R1], в котором лежат только индексы из [L0; R0]. Итого нам придется только двоично спускаться по дереву, поэтому сложность  на запрос.
на запрос.
В целом, fraction cascadinbg используется в задачах на MergeSortTree, в которых требуется каждый раз бинпоиском искать что-то в сыновьях.
3) Научимся решать задачи на запросы в оффлайн, которые вы можете сделать на обычном ДО, но с возможностью добавления и удаления элементов. Для этого нам надо понять относительный порядок элементов, если бы мы не удаляли элементы.
Давайте заведем неявное ДД; для каждого элемента будем хранить 0 или 1 — удален этот элемент или нет соответственно, а так же будем сохранять количество неудаленных в поддереве(еще чтобы в конце выполнить запросы, требуется хранить номера запросов, которые добавили и удалили данный элемент). Тогда напишем ещё одну операцию split1, которая будет аналогично split разрезать дерево на 2, но в split1 будет разрезать по количеству еще не удалённых элементов в правом дереве. Теперь с помощью split1 и стандартного merge мы можем добавлять и удалять элементы(вместо удаления нам просто нужно поставить 0 в элемент на позиции pos среди неудаленных).
Теперь мы получили относительный порядок элементов, можно построить дерево отрезков и выполнять наши операции, а вместо удаленных или еще недобавленных элементов можно записать фиктивные значения.
Сложность построения: 
В целом, эта мини-лекция была подготовительной для дальнейших и является базовой и необходимой в олимпиадном программировании.
Если что-то не понятно, задавайте вопросы в комментариях, объясню более подробно











Кажется, во втором пункте вы загнали лажу.
Я обновил описание l и r по-другому: l[i] означает количество элементов в левом поддереве, которые не больше a[i], аналогично c r. Тогда становится понятно, что с помощью такой информации можно восстановить новые индексы при переходе в левое и правое поддерево, означающие upper_bound от l и r. Нужно только разобраться с +-1
Я в начале невнимательно прочитал и ошибся, на самом деле решение работает :)
По поводу fractional cascading: нужно чётко понимать, что этот алгоритм скорее теоретический и в реальности работает медленно (хороший log ^ 2 быстрее).
Подробнее: https://codeforces.net/blog/entry/21892
Нет, у fractions cascading абсолютно нет константы, поэтому там log. Например в иннополисе именно k-тую статистику не сдать без этой оптимизации.
Ну, насколько я помню, я смог запихать туда фенвика (правда уже после того, как FC написал). То что говорит Вова — имееет смысл, опять таки — у тебя в целом достаточно плохая реализация алгоритма за log * log.
Более того, мне на реальной олимпиаде попадалась задача, которая без fractional cascading в онлайн не заходит