Hi Codeforces!
This is the editorial of Codeforces Round 482 (Div. 2). I hope you guys enjoy it.
If n = 0, the answer is obviously 0.
If n + 1 is even, we can make 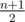 diametric cuts. Otherwise, the only way is to make n + 1 cuts.
diametric cuts. Otherwise, the only way is to make n + 1 cuts.
Time complexity: O(1).
#include <stdio.h>
using namespace std;
long long n;
int main()
{
scanf("%I64d", &n);
n++;
if (n == 1) printf("0"); else if (n % 2 == 0) printf("%I64d", n / 2); else printf("%I64d", n);
return 0;
}
We all knew that the substrings with length 1 appear at most in the string. So, to make a string as beautiful as possible, we will choose the letter that firstly appears at most in the string and replace all the other letters with the chosen letter.
There is some cases. If n is less than or equal to the number of remaining letters, just add n to the beauty. If n is even after replacing all letters with the chosen, we can choose an arbitrary letter, replace it with some other letter, return it back and repeat the work till n reach 0. Otherwise, we will not replace all the other letters. Instead, we will replace the letters until there is 1 letter left (now n is even) then replace that one with another letter different from our chosen letter. After that, replace that letter with our chosen letter. Now n is even again, we repeat the work discussed above.
In conclusion, let's call our string s, our chosen letter a and its number of occurrences in the string fa, then our answer is min(fa + n, |s|). Be careful with n = 1.
Time complexity:  , where
, where  is the total length of the three strings.
is the total length of the three strings.
#include <bits/stdc++.h>
using namespace std;
int a[256], b[256], c[256], n, ma, mb, mc;
string p, q, r;
int main() {
cin >> n >> p >> q >> r;
for (char x: p) ma = max(ma, ++a[x]);
for (char x: q) mb = max(mb, ++b[x]);
for (char x: r) mc = max(mc, ++c[x]);
if (n == 1 && ma == (int)p.length()) p.pop_back();
if (n == 1 && mb == (int)q.length()) q.pop_back();
if (n == 1 && mc == (int)r.length()) r.pop_back();
ma = min(ma + n, (int)p.length());
mb = min(mb + n, (int)q.length());
mc = min(mc + n, (int)r.length());
if (ma > mb && ma > mc) {
puts("Kuro");
return 0;
}
if (mb > ma && mb > mc) {
puts("Shiro");
return 0;
}
if (mc > ma && mc > mb) {
puts("Katie");
return 0;
}
puts("Draw");
return 0;
}
979C - Куро и прогулочный маршрут
We can consider the city as a graph, in which every town is a vertex and every road connecting two towns is an edge. Since m < n, we can deduce that this graph is a tree. Now, instead of finding the number of pairs that Kuro can choose, we can find the number of pairs that Kuro cannot choose. In other words, we must find the number of pairs of vertices (u, v), in which the shortest path from u to v passes through x and then through y. But how can we do this?
If we take vertex y as the root of the tree, we can see that every pair of vertices that Kuro cannot choose begins from any node within the subtree of node x, and finishes at any node but within the subtree of node z, which z is a direct child of y lying on the shortest path from x to y. In total, the number of pairs of vertices that we are looking for is equal of n·(n - 1) - s[x]·(s[y] - s[z]), which s[i] denotes the size of the subtree of node i. We can implement this using simple DFS.
Time complexity: O(n).
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 3e5;
int n, m, u, v, x, y, sub_size[MAXN + 5];
bool vis[MAXN + 5], chk_sub[MAXN + 5];
vector<int> adj[MAXN + 5];
int DFS(int u)
{
vis[u] = true; sub_size[u] = 1;
if (u == x)
chk_sub[u] = true;
else chk_sub[u] = false;
for (int v: adj[u])
if (!vis[v])
{
sub_size[u] += DFS(v);
chk_sub[u] |= chk_sub[v];
}
return sub_size[u];
}
int main()
{
scanf("%d%d%d", &n, &x, &y);
m = n - 1;
while (m--)
{
scanf("%d%d", &u, &v);
adj[u].push_back(v);
adj[v].push_back(u);
}
DFS(y);
long long fin;
for (int v: adj[y])
if (chk_sub[v])
{
fin = sub_size[y] - sub_size[v];
break;
}
printf("%I64d", 1LL * n * (n - 1) - fin * sub_size[x]);
return 0;
}
979D - Куро, НОД, побитовое исключающее ИЛИ, сумма и все-все-все
We first look at the condition 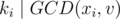 . This condition holds iff both xi and v are divisible by ki. Therefore, if
. This condition holds iff both xi and v are divisible by ki. Therefore, if 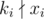 , we return
, we return -1 immediately, else we only consider numbers in a that are divisible by ki.
Finding the maximum XOR of xi with v in the array a reminds us of a classic problem, where the data structure trie is used to descend from the higher bit positions to the lower bit positions. But since we only consider v such that 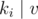 and xi + v ≤ si, we build 105 tries, where the ith trie holds information of numbers in a that are divisible by i, and we only descend to a branch in the trie if the branch is not empty and the minimum value in the branch is ≤ si - xi.
and xi + v ≤ si, we build 105 tries, where the ith trie holds information of numbers in a that are divisible by i, and we only descend to a branch in the trie if the branch is not empty and the minimum value in the branch is ≤ si - xi.
Adding a number into a is trivial by now: we update every uth trie where u divides the number we need to add into the array. Notice that we only add a number if the number doesn't exist in the array yet.
Time complexity: O(MAXlog(MAX) + qlog(MAX)2).
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int MAX = 1E5 + 5;
struct SNode
{
int mi;
SNode *bit[2];
SNode()
{
mi = MAX;
bit[0] = bit[1] = nullptr;
}
} *rt[MAX];
vector<int> di[MAX];
int q, t, u, k, x, s;
bool chk[MAX];
void init()
{
for (int i = 1; i < MAX; i++)
{
for (int j = i; j < MAX; j += i)
di[j].push_back(i);
rt[i] = new SNode();
}
}
void add(int k, int u)
{
SNode *cur = rt[k];
cur->mi = min(cur->mi, u);
for (int i = 18; i >= 0; i--)
{
if (cur->bit[u >> i & 1] == nullptr)
cur->bit[u >> i & 1] = new SNode();
cur = cur->bit[u >> i & 1];
cur->mi = min(cur->mi, u);
}
}
int que(int x, int k, int s)
{
SNode *cur = rt[k];
if (x % k != 0 || cur->mi + x > s)
return -1;
int ret = 0;
for (int i = 18; i >= 0; i--)
{
int bi = x >> i & 1;
if (cur->bit[bi ^ 1] != nullptr && cur->bit[bi ^ 1]->mi + x <= s)
{
ret += ((bi ^ 1) << i);
cur = cur->bit[bi ^ 1];
}
else
{
ret += (bi << i);
cur = cur->bit[bi];
}
}
return ret;
}
int main()
{
init();
scanf("%d", &q);
while (q--)
{
scanf("%d", &t);
if (t == 1)
{
scanf("%d", &u);
if (!chk[u])
{
chk[u] = true;
for (int k : di[u])
add(k, u);
}
}
else
{
scanf("%d%d%d", &x, &k, &s);
printf("%d\n", que(x, k, s));
}
}
return 0;
}
979E - Куро и Топологическая четность
The problem asks us to find the number of different simple directed acyclic graphs with 1 → n forming its topological order to ensure the parity of the number of alternating paths to be equal to p. We will solve this problem using the dynamic programming approach.
Let's define even-white as the number of different nodes u colored in white that has an even number of alternating paths that end in u. In the same fashion, let's define odd-white as the number of different nodes u colored in white that has an odd number of alternating paths that end in u, even-black — the number of different nodes u colored in black that has an even number of alternating paths that end in u, and odd-black — the number of different nodes u colored in black that has an odd number of alternating paths that end in u. Let's also define dp[i][ew][ow][eb] as the number of different graphs following the requirements that can be built using the first i nodes, with ew even-white nodes, ow odd-white nodes and eb even-black nodes (the number of odd-black nodes ob = i - ew - ow - eb). We will figure out how to calculate such value. For the sake of simplicity, let's consider the current node — the {i}th node to be a white node.
We can notice a few things:
If none of the previous i - 1 nodes connects to the current node, the current node becomes an odd-white node (the only alternating path that ends the current node is the node itself).
How the previous white nodes connect to the current node does not matter. There are 2ow + ew - 1 ways to add edges between the previous white nodes and the current node.
How the previous even-black nodes connect to the current node does not matter, as it does not change the state of the current white node (i.e. odd-white to even-white or even-white to odd-white). There are 2eb ways to add edges between the previous even-black nodes and the current node.
If there are an odd number of previous odd-black nodes that have edges to the current node, the current node becomes an even-white node. There are
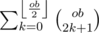 ways to do this.
ways to do this.If there are an even number of previous odd-black nodes that have edges to the current node, the current node becomes an odd-white node. There are
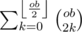 ways to do this.
ways to do this.
In conclusion, we can figure out that:
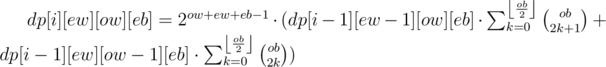
It is worth mentioning that we can use the same analogy to process when the current node is black.
In total, we process through n4 states, with an O(n) iteration for each stage, so the time complexity is O(n5). However, with precomputation of 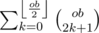 and
and 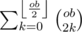 for every value of ob, we can optimize the time complexity to O(n4).
for every value of ob, we can optimize the time complexity to O(n4).
Time complexity: O(n4).
#include <iostream>
using namespace std;
const int N = 55, MOD = 1E9 + 7;
int n, p, c[N];
long long ans = 0, pw[N], fct[N], inv[N], od[N], ev[N], f[N][N][N][N];
long long power(int u, int p)
{
if (p == 0)
return 1;
long long ret = power(u, p >> 1);
(ret *= ret) %= MOD;
if (p & 1)
(ret *= u) %= MOD;
return ret;
}
long long C(int n, int k)
{
return fct[n] * inv[k] % MOD * inv[n - k] % MOD;
}
void init()
{
f[0][0][0][0] = 1;
pw[0] = 1;
fct[0] = 1;
for (int i = 1; i < N; i++)
{
pw[i] = pw[i - 1] * 2 % MOD;
fct[i] = fct[i - 1] * i % MOD;
}
inv[N - 1] = power(fct[N - 1], MOD - 2);
for (int i = N - 2; i >= 0; i--)
inv[i] = inv[i + 1] * (i + 1) % MOD;
for (int i = 0; i < N; i++)
{
for (int j = 0; j <= i; j += 2)
(ev[i] += C(i, j)) %= MOD;
for (int j = 1; j <= i; j += 2)
(od[i] += C(i, j)) %= MOD;
}
}
void find_ans(int ob, int eb, int ow, int ew, int col, long long &ret)
{
// current node is even-white
if (col != 0 && ew != 0)
(ret += f[ob][eb][ow][ew - 1] * pw[ow + ew - 1 + eb] % MOD * od[ob] % MOD) %= MOD;
// current node is odd-white
if (col != 0 && ow != 0)
(ret += f[ob][eb][ow - 1][ew] * pw[ow - 1 + ew + eb] % MOD * ev[ob] % MOD) %= MOD;
// current node is even-black
if (col != 1 && eb != 0)
(ret += f[ob][eb - 1][ow][ew] * pw[ob + eb - 1 + ew] % MOD * od[ow] % MOD) %= MOD;
// current node is odd-black
if (col != 1 && ob != 0)
(ret += f[ob - 1][eb][ow][ew] * pw[ob - 1 + eb + ew] % MOD * ev[ow] % MOD) %= MOD;
}
int main()
{
init();
scanf("%d%d", &n, &p);
for (int i = 1; i <= n; i++)
scanf("%d", c + i);
for (int i = 1; i <= n; i++)
for (int ob = 0; ob <= i; ob++)
for (int eb = 0; ob + eb <= i; eb++)
for (int ow = 0; ob + eb + ow <= i; ow++)
{
int ew = i - ob - eb - ow;
find_ans(ob, eb, ow, ew, c[i], f[ob][eb][ow][ew]);
if (i == n && ((ob + ow) & 1) == p)
(ans += f[ob][eb][ow][ew]) %= MOD;
}
printf("%lld", ans);
return 0;
}











Actually,
Maybe this can simply the dp in E even more...
That is a really nice catch! That is a new thing I learned right from my own contest!
There's a catch -- this formula fails for n = 0. So one needs to be slightly careful there. But otherwise, I believe the dp becomes even simpler.
Edit: In response to Illidan's comment below, our dp state becomes dp [i][ob>0][ow>0] -- as in the boolean values ob>0 and ow>0, so I think we are down to O(n) states. (If I'm not hallucinating)
Actually there are some O(n) solutions and I've written one.
http://codeforces.net/contest/979/submission/39938942 (31ms, 0kb)
and there are many O(n) solutions better than mine. XD
E: all states that matters are oddblack and oddwhite, because even number doesn't change parity. This leads to n3 solution dp[i][ob][ow]
"holds and only holds if" should probably be "holds if and only if"
[sorry for asking but i didn't understand the editorial so i did ask a stupid question]
aaaaa -> aaaab -> aaaac -> aaaaa
4
aaaabcd
aaaabcd
aaaaaaa
Can someone explain why the answer for this case is "draw"?
Since there are four turns first and second one will make the string as aaaaaaa after 3 turns and for the last turn let us assume it is aaaaaab.
The third one will do the following : aaaaaaa-> aaaaaab -> aaaaaaa -> aaaaaab -> aaaaaaa
Since third one has max beauty I think he must win :(
First one: aaaabcd > aaaabce > aaaaace > aaaaaae > aaaaaaa. Second one: same as first one. Third one: aaaaaaa > aaaaaab > aaaaaaa > aaaaaab > aaaaaaa.
So the answer is
Draw.GOT IT :D
[ignore,answered above] made the same mistake.
so it stands as a draw
I ran C in nlogn by rooting the tree at x and then doing LCA queries for all nodes and node y. If the lca of some node i and y was x, that takes out however many nodes are in the subtree of y (including y).
Can someone give a better explanation for B in the case n is odd?
I though that if we had length L for each string and each letter frequency of F[i], then we could say that min(L, F[x] + n) is our "answer" for a letter x, but for the case in which n = L - F[x] + 1, then we would set all the letters of the string to x, with 1 turn left, so this turn will change anyone of the already equal letters, leading to a beauty of L - 1, but in the case n > L - F[x] + 1, one can use what's left to make a cycle for a letter, since its possible.
Tell me what's wrong with this idea, please? D:
If you have a string aaabb and N = 3, you can first change one of the b's to a random other letter, and then change them to a's.
aaabb -> aaaBb
aaaBb -> aaaab
aaaab -> aaaaa
Thanks, I noticed my error. I didn't think about making an uncomplete cycle starting with a different letter than the one I want to set. :D
Tks, at first I thought I could only change twice to make it be back, which leads me to wrong algorithm :(
What if string is aaaaa and n=3. In this case you will get 4 at most. But solution says 5. Can anyone explain this?
Sorry for that. Got my mistake. It's like aaaaa -> baaaa -> caaaa -> aaaaa
Problem C TLE. Is this 38236023 not O(n)? Poor python coder!
It's n^2. See the lines
path = path + [vs]andif v not in path.Alright those operations on
pathare questionable, so I redid thefind_pathto be totally like my DFS for counting the subtree size: 38269505 Still TLE though!I have solved C in O(n) also but in another way, first find the shortest path from x to y (simple BFS), lets say the shortest path is x > a > b > y, then we remove the edge (x, a) and start DFS from x to count how many nodes behind x (including x itself), define it as xCnt, then do the same thing with y, remove the edge (y, b) and start DFS from y to count how many nodes behind y (including y itself), define it as yCnt.
Finally the solution is n * (n - 1) - xCnt * yCnt.
To remove the edges quickly we can set nodes a and b visited before start the DFS.
Thanks for explaining your approach. This pretty much is what I did as well
Here is the same approach, but using only DFS.
I did something completely different (rooting the tree at y, counting subtree size of x, rooting at x, counting subtree size of y) and I got the same formula. Interesting
In problem D, there is no need to bother for Trie. You can pick a Set and do binary search on it by holding a binary-form-prefix of desired xor(which is already found in set) on each iteration.
I got accepted on D with a kinda weird solution, O(n**2), I believe.
Basically for each number [1...1e5] I have its divisors in a vector (this can be calculated in O(n log n)).
As a primary data structure I have a vector (of size 1e5) of sets.
Now, for each type-1 query x I loop through its divisors d (from that vector) and add x to set with index d (so that I know which numbers in array satisfy condition k | x).
For each type-2 query on the other hand, I run an upper_bound on k-th set with s — x and go to the set's beginning. In other words, I loop through elements in array divisible by k, non greater than s — x, this is obviously O(n) for a type-2 query and with this implementation I got TLE. What made this solution accepted was an additional condition "if currently checked multiply of k plus x is less than current-best" then I stopped checking lesser candidates.
Why is this correct? One may prove that a ^ b <= a + b, so if v + x < current-best then we are not able to find better solution, so we can stop searching for it. I am afraid though that this solution is only (in a worst case scenario) two times faster than the original one. But surprisingly it is accepted.
For a reference you may see my submission 38240724. I know it is not a very clean code.
a ^ b <= a + b, that's another nice property of xor. I'll make sure to remember it. Thanks!If I undestood all correctly, complexity of D in editorial should be O(MAXlog(MAX)2 + qlog(MAX)), because each second query is calculated in log MAX, and for the first queries we are using estimation that number of pairs (x, y), such that x | y is MAX + MAX / 2 + MAX / 3 + ... + MAX / MAX = O(MAX ln MAX). Because individual first query can be added in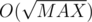 tries. Beatiful idea, btw.
tries. Beatiful idea, btw.
However, my solution, that doesn't check, if we added the same number earlier, and for which this estimation can't be apply and we can make it each time look at all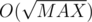 tries (I used
tries (I used
std::setinstead of trie) passed all tests too (may be weak tests?).Also, this problem can be solved by using
std::setinstead of trie and usinglower_boundfor each bit calculation. Then second part of complexity would be qlog(MAX)2 (code example, same link as above).Задача D. Официальное решение выполняется 20х раз медленнее чем самое быстрое решение!!!
http://codeforces.net/contest/979/submission/38236267 46 мс.
http://codeforces.net/contest/979/submission/38249326 904 мс.
I don't understand what you wrote, but that 46ms solution looks like brute force with a break to stop checking.
It seems like a brute force searches all number that can be divided by k and only breaks when found v - x > i + x, which means for all j < i ,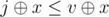 (
( means XOR) because
means XOR) because 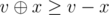 and
and 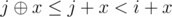
So it seems that the data q = 100000 and t = 2 k = 1 x = 1 s = 100000 with no number added can make this program search O(q2) times.
I"m having trouble figuring out how many nodes we have in the trie. I created one trie using an array with the 105 tries as children of the "root". I tried multiple values for the size of the array (number of nodes), but none of them worked. In the end, I chose a large value that fit in memory (2·107) and it passed. How do you determine how many nodes there are in the worst case? Thanks!
First, let's calculate maximum count of operations "add number to trie". If we add all numbers from 1 to 105 operations count will be equal to the count of different pairs (x, y), such that x | y and y ≤ 105. This count is equal to ⌊105⌋ + ⌊105 / 2⌋ + ⌊105 / 3⌋ + ... + ⌊105 / 105⌋ (count of pairs (1, y), (2, y), (3, y), ... (105, y) respectivly). This expression is smaller than 105·(1 / 1 + 1 / 2 + 1 / 3 + ... + 1 / 105), which is almost equal to 105·ln 105 (see harmonic serie). Or you can just calculate this expression on PC.
And each operation "add number to trie" creates no more than 17 new nodes (17 binary digits). So overall it can be estimated as 105·ln 105·17 ≈ 2·107.
Problem D is really hard for java to get rid of TLE, I failed and turned to C++.
I would like to present an alternative solution to D. Note that, for those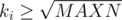 , there are at most
, there are at most 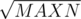 vi candidates, so we can enumerate all these candidates. This can be easily done by using a hashtable. When ki is small, the main problem is that there are too many candidates, a brute-force enumeration will get TLE. We may use some data structures, such as BIT, for each small k, to maintain the occurrence of multiples of k, and use binary search to find the solution. This can be done in
vi candidates, so we can enumerate all these candidates. This can be easily done by using a hashtable. When ki is small, the main problem is that there are too many candidates, a brute-force enumeration will get TLE. We may use some data structures, such as BIT, for each small k, to maintain the occurrence of multiples of k, and use binary search to find the solution. This can be done in 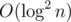 (a good implementation may take only
(a good implementation may take only  I think, but
I think, but 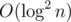 is enough here). This does essentially the same thing as Trie (which I didn't come up with during the contest), but they are different tools.
is enough here). This does essentially the same thing as Trie (which I didn't come up with during the contest), but they are different tools.
I have solved C in O(n) in another way. First dfs from X, recording the size of each nodes' subtree and parent of each nodes in the process of dfs. Then, we find the son of X which is on the shortest path between X and Y (just the highest parent of Y which is not X, and we can find it by the recorded parents), and denote it by Z.
Finally the solution is n * (n - 1) - (size[X] — size[Z]) * size[Y]
I solved D using square rooted N tries.
How did N tries passed without 'Memory Limit Exceeded'?
Use new or malloc and pointers to build tries rather than array?
Implementation of B is really good. Just 9 lines of code and you handled all corner cases. I messed up with n=1. Learned something new today!!
I know . I know . It may sound very strange that someone has got an error in first question. But, i got wrong answer for it. I followed the same approach as described in tutorial .
Here is the link to my code in python3.
For input 822981260158260519 , adding 1 and diving by 2 results in 411490630079130240 whereas the correct answer should have been 411490630079130260.
It would be great help if someone can tell me what's wrong with it. I am not able to figure it out.
Maybe you should use long long?Since the range is greater than int.
There is no limit to value of integers in python3. So, there is no concept of long or long long in python3.
I use python2 and I get accepted! XD
The same code
Maybe you lose too much of a precision when dividing in float numbers? Try using integer division (//).
Thanks awoo for pointing that out. Yeah, it does lose precision when dividing in float numbers. But "how" and "why" questions made me curious to read the python3 docs in detail.
I read the python3 documentation on floating point. I have tried to list down the concepts understood on floating point and division point by point in python3 after reading from various sources below:
sys.float_info.dig) for a. So, here is the catch . The float numbers having significant digits greater than 15 digits will lose some precision while represented as float numbers.Let me try to show that using an example. I will add int with float.
int + float = float . So, i will try to push the limits of floating point arithmetic.
More examples
Thus we can see that it is not safe to represent integers as float .
Now, let's talk about easy way to tackle this kind of problem.
Now coming to test case 11 for problem 979A-38 .
Input: n = 822981260158260519 Now , (n+1)/2 would first convert n+1 as float But 822981260158260519 + 1 converted to float is 8.229812601582605e+17.
Let's check in interpreter.
Summary: Use '//' integer division for these kind of problem. '/' may work fine with numbers having significant digits less than 16.
Notes:
Can someone please tell me why am I getting wrong output here (test case 5) in problem C ? http://codeforces.net/contest/979/submission/38264299
Hi! The problem is in line
t = n*(n-1), because n is an int, but the multiplication produces overflow. If you cast n to long, you'll get AC. If you want, you can check my submission :)E seems to be a very tough problem to me. How to come up with such recursive structures, any insight/ ideas from anyone?
Problem E is 101 or 010 an alternatives path?
Is there a 2eb in the longest equation in solution for E?
UPD: the author has fixed it
2 abcabcabcabcabcabcabcabcabcabcabcabc aaaabbbbccccaaaabbbbccccaaaabbbbcccc ababababababababababababcccccccccccc
Can someone tell me, what will be the beauty of each of the ribbons?
Hi, can any one tell me why this solution for problem C is wrong ?
http://codeforces.net/contest/979/submission/38786238
I'm coloring three types of nodes
nodes in sub_tree of X color 1 nodes in sub_tree of Y color 2
and other nodes will be in color 3
the answer will be n*(n-1) — (nodes of X * nodes of Y)
I found myself stuck in problem D on the 13 test data.
It TLE 4 times there.
Could anyone tell me some tips about this?
submission
I have implemented exactly what the editorial said in Div2D, I have kept the variables also same and still getting TLE in JAVA here is my code
all we care is the parity of ob and ow , so we can dp it in mod 2
and if we know the parity of ob and ow , we can determine how to transmit
the complexity is O(n)
see my code for details http://codeforces.net/contest/979/submission/48867508