Как все решали А? Наше решение работает локально ОЧЕНЬ долго.
Мы одни получали странный вердикт "файл не найден"? UPD: Fixed.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 146 |
Как все решали А? Наше решение работает локально ОЧЕНЬ долго.
Мы одни получали странный вердикт "файл не найден"? UPD: Fixed.
| Название |
|---|



Как решается C??? TL-2....
Линейная динамика. Проверяем, можно ли представить префикс. Пересчет — за константу, смотрим, есть ли переход по s[i] или s[i-1]s[i]
А вы пробовали его на сервер посылать? У нас зашло решение работающиее за O(n * 2n)
P.S. По крайней мере, мы не умеем доказывать, что оно работает быстрее :)
у нас зашел n^2 на 2^ n
А у нас зашло решение O(n^2 * 2^n). n^2 чтобы поддерживать информацию о долгах. Правда мы память не чистили, а хранили номер теста, на котором пришли в это состояние.
У нас тоже O(2n·n), но оно и локально очень быстро работало (с отсечкой "если текущее множество небанкротов является подмножеством уже найденного ответа — выйти из этой ветки рекурсии").
Нафига так жить... Мы пытались meet-in-the-middle
Кто умеет решать F? Всё что мы смогли придумать, — переписать задачу в виде линейной программы, заметить что ограничения имеют вид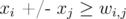 , вспомнить, что такое делается потоком. Но поток там стоимостной, что на таких ограничениях слишком сурово...
, вспомнить, что такое делается потоком. Но поток там стоимостной, что на таких ограничениях слишком сурово...
Мы пытались сдать следующее:
Заметим, что можно считать, что из столицы есть ребро в каждую вершину, по длине равное в точности минимальному пути между столицей и этой вершиной. Пусть ребра в вершины 0 и 1 имеют длины x и y соответственно, тогда ограничения на длину ребер в остальные вершины — несколько линейных от x и y выражений (правда, парочку мы потеряли, скорее всего из-за этого и было WA), которые как раз соответствуют условиям на "кратчайшесть" проведенных ребер и на то, что должно быть невыгодно срезать через столицу путь в вершинам 0 и 1. Из всех этих условий берется максимум, он складывается по всем вершинам, получается выпуклая от x и y функция, для x запустим тернарник, а y можно найти явно, посмотрев на корни производной.
С каких пор у нас 100.000.000.000 операций проходит в 5 секунд? Что за манера давать мультитестирование и не давать макстест? Из-за этого в самом начале контеста динамика по подмножествам отбрасывается, как бредовая и придумывается какой-то meet-in-the middle или эвристика типа алгоритма муравья, которая конечно WAшит. Авторам задачи (или тестов) жирный минус.
Насколько я понимаю, это вполне нормально для CEPC. У них каждый год в какой-нибудь задаче выясняется, что ограничения в условии сильно больше ограничений в тестах, либо как в этот раз: макс. тестов неоправданно мало. Мы, кстати, тоже сломали мозг и только через три часа решились написать долгое решение.
Надо было клар об этом делать!
Как решалась задача E ?
По заданному набору операций строим дерево. Теперь нужно для вершины говорить, можно ли операциями в ее поддереве набрать определенную строчку. Будем от левого сына просить максимальный префикс, от правого — все остальное. + Не будем ходить в поддеревья, где не встретится первая буква слова, которое хотим найти. Набор букв в поддереве заранее посчитаем.
Как решать B и G?
G. Оптимальная область либо простирается вверх в бесконечность, либо с трех сторон упирается в точки одного цвета. Переберем, в какую точку отрезок упирается сверху. Когда такая точка зафиксирована, левая и правая граница определяются однозначно. Чтобы быстро искать эти границы, будем перебирать верхнюю точку снизу вверх и поддерживать для каждого цвета set иксов уже пройденных точек. Тогда левую и правую границу можно найти как lower_bound и upper_bound-1 в соответствующем сете. Искать количество точек между полученными границами можно деревом отрезков. Случай, когда отрезок выше всех точек, можно рассмотреть отдельно практически так же, как случай, когда он куда-то упирается (наверно даже можно отдельно не рассматривать, а отделаться добавлением фиктивных точек сверху).
В В можно погенерить все умирающие последовательности для маленьких n и заметить закономерность.
Ох я себе слабо представляю как на контесте такую закономерность искать, я вон дома времени валом потратил) Может кто-то решил аналитически? Или там жутчайшая математика?)
Мы сгенерировали все "умирающие" последовательности длиной до 23. Сначала обратили внимание на их количества. Для нечетных n они получаются 2 8 2 128 2 8 2 32768 ... Ясно, что все зависит от степени 2, которая входит в n + 1. Дальше посмотреть сами последовательности для 3 и 11 (которых по 8 штук) и понять, как одни получаются из других. Для 7 и 23 закономерность подтверждается. Ничего сложного. Мы на этапах Кубка и не такие закономерности находили.
Спасибо, примерно так же рассуждал, только попутно уходил в сторону от ответа постоянно
У нас вроде бы "аналитически". Посмотрим на 2 шага процесса — понятно что на нечётные позиции результата влияют только нечётные позиции исходного состояния, то же самое для чётных. Посмотрим на чётные и нечётные позиции отдельно: для чётных получаем ту же самую задачу в 2 раза меньшего размера, для нечётных — почти ту же самую; так что если разобраться с нечётными — задача решена. Как с ними в точности разобраться — не знаю, у нас это сделал Jacob (но он это сделал очень быстро, так что наверное что-то несложное).
Для нечётных надо сделать один ход, и они станут чётными.
Сделаем бесконечную строку v = ... + 0 + s + 0 + reverse(s) + 0 + s + 0 + reverse(s) + 0 + .... Если за si и vi обозначить соответствующие строки после i шагов, то vi = ... + 0 + si + 0 + reverse(si) + 0 + ...
Легко доказать по индукции, что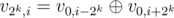 . Поскольку v периодическая с периодом 2|s| + 2, можно взять достаточно большую степень двойки k (например, k = 2|s| + 3) и проверить, что в v2k есть хотя бы одна единица. Если использовать предыдущее равенство, это делается за O(|s|).
. Поскольку v периодическая с периодом 2|s| + 2, можно взять достаточно большую степень двойки k (например, k = 2|s| + 3) и проверить, что в v2k есть хотя бы одна единица. Если использовать предыдущее равенство, это делается за O(|s|).
WA1 в M. Код:
Как это понимать?
Код даёт ОК на g++0x. На другом — ВА1.
Спасибо. Это же какие кривые тесты в этой задаче... Мало того, что не сдал халяву, так и ещё время потратил впустую.
Так всё же в чем тут ошибка?
Возможно из-за функции модуля. Стандартный все считает в даблах. А у вас потом еще и тип приводится к целому. Попробуйте отослать с самописным модулем.
Стандартный все считает в даблах.
Неправда, std::abs имеет несколько перегрузок.
Да нет, в интах он считает, есть перегрзка для лонг дабла и коплексных, а вот для лонг лонга нет.
Хорошо. Тогда прошу кого-нибудь объяснить, почему зашел вот такой код, почти полностью совпадающий с вашим
UPD. И еще. Было несколько раз, что код, в котором я юзал стандартный модуль с интами, просто не компилился на сервере. А в логах было написано, что у него нету функции для вызова такой штуки.
Вставляем любую некомпилирующуюся строку после цикла, и смотрим варнинг компилятора на сервере: 002841.cpp: In function 'int main()':
002841.cpp:13:45: warning: format '%d' expects argument of type 'int', but argument 2 has type 'double' [-Wformat]
Т.е. int abs(int) это не стандарт?
В референсе написано, что у него действительно есть несколько перегруженных функций для модуля. Но вот как-то работает это криво. Я думаю он берет первую, которую видит и приводит типы. Такой вот выстрел себе в ногу, ведь язык допускает такую возможность. Гарантировать правильность моего объяснения я не могу, но это единственный логичный вывод, который я могу сделать.
UPD. Порылся в исходниках cmath. Вот начало библиотеки, и сначала там действительно идет модуль для вещественных чисел. Честно говоря, для интов модуля я там не нашел вообще. Возможно он где-то там зарыт в шаблонах, но как-то совсем на это не похоже. Нужна консультация более прошаренного специалиста :)
Ага, причем на g++0x варнинга нет. Кривой g++?
Если в коде вставить
, где объявлен
abs(), то предупреждение пропадает. Сюрприз!Ну в этом как раз нет нестыковок, там все-таки другие реализации большой кучи функций. Увы, в этом плане g++ действительно кривоват. Такая же фигня, кстати, со стандартным возведением в степень. Была ситуация, когда на больших числах порядка 10^15, pow мне говорил: "Не, чувак, тут тебе не нужна плюс единичка, я ее выкинул". Точнее он этого не говорил, пришлось выпытать это у него. Сопротивлялся он долго и упорно, поэтому остался осадок. Теперь стараюсь такие стандартные функции, пришедшие из C, не использовать.
pow()работает с числами с плавающей точкой, какие к нему вопросы? Кстати, для целочисленного возведения в степень в GCC есть нестандартная функция__gnu_cxx::power()(<ext/numeric>).К нему вопросов никаких :) А про то, где находится интовый abs, спасибо :)
Спасибо, действительно неприятный сюрприз. В VC++ интовый abs объявлен в cmath, я думал и в g++ так. Оказалось, что в cmath g++ объявлены abs'ы для вещественных аргументов, а в cstdlib для целых (в том числе и для long long).
Вот мне тоже интересно, написал аппеляцию, мне ответили:
Первый тест совпадает с тестом из условия.
Как решать D?
Последовательность является нудной, если существует подотрезок, в котором все числа встречаются более одного раза. Переберем правый конец этого подотрезка и попробуем найти соответствующий левый. Если нам это не удастся ни для какого правого конца, то последовательность не является нудной.
Итак, у нас фиксирован правый конец (пусть он имеет индекс R) и мы уже обработали все числа, которые стоят слева от него. Для каждого числа возьмем последние 2 его вхождения — пусть у числа X позиции вхождений x1 и x2 (x1 < x2). Тогда на место x1 запишем -1, а на место x2 запишем 1. На месте всех остальных чисел у нас будут стоять нули. Тогда утверждается, что существует нудный подотрезок тогда и только тогда, когда суффикс подмассива [0,R] с минимальной суммой имеет нулевую сумму.
Итак, нам нужно уметь делать изменение в точке, а также для отрезка [0,A] быстро находить суффикс с минимальной суммой. Это можно сделать обычным деревом отрезков. Сложность решения O(NlogN).
Если отрезок интересный, то на нем должен быть уникальный элемент. Он разобьет отрезок на две меньших подзадачи. Сложность только в том как найти уникальный. Я для этого передавал в рекурсию, кроме концов отрезка, map, где хранил сколько раз каждый элемент входит в данный отрезок, а также очередь с уникальными элементами. Получили две подзадачи. Выбираем меньшую и для нее map считаем в лоб, проходя по всем элементам. Также проходя по всем элементам меньшего подотрезка обновляем map для большего. Итого вроде получается O(Nlog^2N)
Мы такое сдали:
Строка не является нудной, если для любой ее подстроки существует символ, встерчающийся на ней ровно один раз.
Будем связывать подстроку
s[l..r]с клеткой на плоскости с координатами(l,r).Пусть
L[i]— индекс ближайшего слева символа такого же какs[i](или-1, если такого нет), аR[i]— индекс ближайшего справа (len(s), если такого нет).Для каждой позиции исходной строки найдем множество подстрок, на которых символ этой позиции встречается ровно один раз. Искомое множество для
s[i]— подстроки, начинающиеся на[L[i]+1; i]и заканчивающиеся на[i; R[i]-1]. Получился прямоугольник из клеток для каждой позиции. Строка не является нудной, если объединение таких прямоугольников покрывает все множество подстрок (которое выглядит как лесенка). Найдем площадь объединения этих прямоугольников. Если она равнаlen(s)*(len(s)+1)/2— строка не нудная.а J только за MlogN решалась?
У нас решение за O(N + M). Выбираем начальную лабораторию. Далее, для каждой работы определим сколько еще зависимостей надо выполнить перед ней (напрямую связанные с ней). Те, у которых зависимостей нет, кидаем в одну из двух очередей, в зависимости от номера лаборатории. Затем, пока очередь с текущей лабораторией не пуста, достаём из неё работу, выполняем, и обновляем количество зависимостей у соседей. Если у соседа стало 0, добавляем его в соответствующую очередь. Как только очередь стала пустой, меняем лабораторию и продолжаем.
Придумали так же, только с деком, но не придумали как решать для кучи компонент связности. Расскажите, пожалуйста, как это сделали вы.
Так это никак не влияет, изначально в очередях вершины без зависимостей со всех компонент. Вот код.
Тоже решение за M + N:
Создадим виртуальный корень — вершину от которой все зависят, переберм ее цвет.
Теперь запустим дфс для всех вершин, выберем максимум. Ответ для вершины — максимум из (ответ для зависимости + [цвета разные?1:0])
Кто подскажет, как решать К?
Говорят, что там такое решение: каждое дерево, удовлетворяющее условию и имеющее K листьев, однозначно разбивается на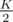 вершинно-непересекающихся путей, концы которых находятся в листах. Найдем такое разбиение для обоих деревьев и проверим, получился ли в результате гамильтонов цикл.
вершинно-непересекающихся путей, концы которых находятся в листах. Найдем такое разбиение для обоих деревьев и проверим, получился ли в результате гамильтонов цикл.
Не каждое дерево разбивается. Если не разбивается, то ответа нет. Разбить и проверить разбиваемость можно одним обходом в глубину, возвращая из поддерева путь в единственный непоматченный лист.