radoslav11's blog

Bubble Cup 2018 Round 2 — Neo
By radoslav11, history, 6 years ago, In English

Hello!

Bubble Cup 2018 Round 2 just finished, so I decided to ask about a correct solution problem NEO. I guess a lot of people passed it in 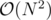with the C++ pragma optimizations or with some greedy optimizations. My team also passed it like that.

In this blog I'll share my idea. If someone has solved it in a similar way I will really appreciate if he shares his code because honestly the idea is really annoying to implement. If anyone has another solution, which is better than 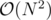I will really love to know the idea.

So the solution I had in mind is 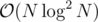or 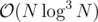depending how we implement our query. First we will have the standard DP: dpi = maxj < i(dpj + sumi * i + sumj * j - j * sumi - i * sumj) which can be reformed to dpi = sumi * i + maxj < i((dpj + sumj * j) + ( - j * sumi) + ( - i * sumj)). Well we can still reform this equation the the following: .

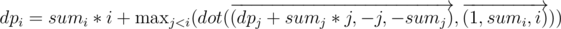Now basically we only need to implement a data structure for the following operations:

  1. Add a vector to our DS.

  2. Given a vector, find the one with the largest dot product, when multiplied with it.

I found a paper which claimed that the following operations can be implemented with a 3D convex hull and another one which claimed that these operations can be converted to dynamic furthest point search, but unfortunately I cannot find the latter again (this happens when you do not bookmark anything). Also both presented data structures/algorithms were really annoying to implement.

So has anyone solved this problem in a legit way and if yes, can he share his solution. Thanks in advance :)

  • Vote: I like it
  • +50
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +16 Vote: I do not like it

I think some ideas from here are usable Maximum (sum × length) subarray problem

→ Reply
»
6 years ago, # |
  Vote: I like it +24 Vote: I do not like it

Another relevant discussion.

→ Reply
»
6 years ago, # |
  Vote: I like it +21 Vote: I do not like it

My solution on SPOJ is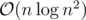 . It applies the transformation you described to reduce the problem to dynamic incremental 3D extreme point queries.

For the DS, I use the static 3D convex hull algorithm from the paper "A Minimalist's Implementation of the 3-d Divide-and-Conquer Convex Hull Algorithm" by "Timothy M. Chan", adapted for dealing with some degeneracy. The paper has a small section about extreme point queries, my implementation uses persistent treaps for it.

To deal with insertions, I maintain DS of exponentially increasing sizes (1, 2, 4, 8, ...) where I insert a vector as a hull of size 1 and then merge DS of equal sizes by rebuilding the hull.

The main bottleneck was the construction of the convex hull (the algorithm has a large constant), so I optimized that part to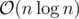 by merging DS with a single linear-time conquer step.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    How to solve static 3D extreme point queries with convex hull?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      The algorithm in the paper creates the convex hull in a form that is suitable for 3D extreme point queries. If I remember correctly, it computes a sweep line along t where it (implicitly) produces the intersection of the hull with the plane z = yt. The sweep-line events are computed via divide-and-conquer along the x-direction. (You might want to read the paper for a better understanding.)

      To query an extreme point, compute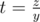 , get the implicit representation at time time point (this is where persistency is used, as we need to remember this at all time points) and query a 2D extreme point in the representation (ternary search, just like finding an extreme point on a 2-dimensional convex hull).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Thanks!

        The idea in the paper is really neat. Can you please share your code as both in your comment and in the paper I didn't get the whole idea for the extreme query point (the ternary search part).

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +21 Vote: I do not like it

          The code is kind of a mess, as I optimized different parts of it over time. Feel free to ask questions if you don't get a certain part.

          Code
          → Reply
»
6 years ago, # |
  Vote: I like it +26 Vote: I do not like it

NEO was a brilliant problem ruined by crappy test cases...

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    :'(

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Maybe, just for the record, everyone could write what kind of stupid 'optimization' squeezed his O(N^2) solution to pass :)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      I did:

      If there two adjacent nonnegative numbers, they will always be in the same final block. So just compact all sequences of consecutive nonnegative numbers and have a (sum, count) pair for each element instead of just value. Then do the straightforward O(N2) dp. Passed.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      My solution: Observe that the optimal solution is going to be composed of number of larger blocks with positive sums, and single negative element blocks, and that there won't be two consecutive blocks of first kind.

      Then, I either have a single element block, or a block [j...i] for which optimal solution to [1...j - 1] consists of single negative element j - 1.

      Taking that into account, straightforward DP in O(N2) passes.

      → Reply