250A - Бумажная работа. Будем действовать жадно — а именно, формировать каждую следующую папку с бумагами так, чтобы она включала в себя как можно больше бумаг. Закончить формирование папку следует сразу же перед 3м убыточным листом, или же при достижении конца массива. Несложно доказать, что такая стратегия оптимальна. Итого решение за O(n).

Автор — MikeMirzayanov

. 250B - Восстановление IPv6. Сначала разобьем строку на подстроки, используя ":" как разделитель. Из всех вхождений пустой строки (они все будут входить подряд, поскольку "::" встречается не более 1 раза) оставим только одно. Теперь мы может определить на какое число нулевых блоков следует заменить пустую строчку. Заменяем. Теперь выводим ответ, дополняя все подстроки ведущими нулями так. чтобы длина каждой подстроки стала равна 4.

Автор — Ripatti.

250C - Кинокритика. Рассмотрим какой нибудь максимальный по включению отрезок фильмов, скажем, жанра x (от 1 до k). Посмотрим как изменится число стрессов, если этот отрезок удалить. Если отрезок прилегает к границе массива a, то после удаления будет достигнуто улучшение +1. Отрезок не может прилегать сразу к 2м сторонам массива, поскольку k > 1. Если этот отрезок (скажем, [i, j]) внутри массива, то давайте посмотрим на a_i - 1 и a_j + 1. Если они равны, то после удаления будет достигнуто улучшение +2; иначе улучшение будет +1.

Теперь пройдемся по всем максимальным по включению отрезкам фильмов одного жанра и найдем улучшения для каждого из них. Сгруппируем отрезки по жанру, значения улучшений для каждой группы сложим. Ответом будет являться номер жанра, для которого суммарное улучшение оказалось максимальным (если таких несколько, то, по условию, выберем минимальный номер жанра).

Описанное выше решение можно реализовать за O(n).

Авторы — MikeMirzayanov Gerald Ripatti.

250D - Постройка моста. Для каждой точки восточного берега будем искать оптимальную точку на западном берегу. После этого выберем оптимум по всем точкам восточного берега.

Хорошо, пусть мы зафиксировали j-ую восточную точку (1 ≤ j ≤ m). Теперь посмотрим как меняется суммарное расстояние в зависимости от выбора точки на западном берегу. Среди всех точек лучшим оптимумом будет точка пересечения прямой OB_j и x = a: 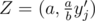, однако этой точки может не оказаться среди доступных для выбора. При перемещении на север или на юг суммарное расстояние пути будет увеличиваться, поэтому среди кандидатов следует рассмотреть только ближайшие к Z точки с севера и с юга.

Найти искомые точки для каждой Z можно с помощью бинпоиска. Еще можно воспользоваться тем фактом, что при увеличении j, точка Z всегда движется в одном направлении; поэтому ближайшие к Z точки можно поддерживать с помощью указателя. Еще можно вообще не рассматривать точку Z, а взять за основу тот факт, что функция расстояния при перемещении точки по западному берегу в одном направлении сначала увеличивается, а затем уменьшается (этот факт показан в предыдущем абзаце); тогда для поиска оптимума можно воспользоваться тернарным поиском.

Итого, у данной задачи есть решения за O(m + n) и .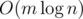

Автор — Ripatti.

250E - Безумный Джо. Будем моделировать весь процесс. Случай бесконечного блуждания можно отловить если на каждом этаже отслеживать с какой стороны мы ударялись в бетонные блоки. Если были удары и слева и справа, то мы зажаты между какими то двумя бетонными блоками и следует вывести Never.

Моделирование в лоб может продолжаться очень долго. Такое решение имеет сложность O(nm²) и ответ может быть порядка 10¹⁰. Поэтому моделирование нужно ускорить, например, следующим образом.

На каждом этаже будем хранить отрезок клеток, в которых мы уже побывали. Нам известно, что под всеми клетками этого отрезка непустые клетки. Поэтому каждый раз, когда мы разворачиваемся, мы можем за O(1) пройтись по всему отрезку сразу. Такая оптимизация улучшает оценку решения до O(nm) — мы каждый раз после одной или двух "телепортаций" либо расширяем границы отрезка, либо переделываем кирпичную клетку в пустую, либо падаем вниз, а всего каждого из действий мы можем сделать не более nm раз.

Автор — Ripatti.