Все задачи подготовлены нами — gop2024 и ----------.
(Идея задачи — gop2024)
Tutorial is loading...
Код — 39423470
(Идея задачи — GreenGrape)
Tutorial is loading...
Код — 39423481
(Идея задачи — ----------)
Tutorial is loading...
Код — 39423497
(Идея задачи — gop2024)
Tutorial is loading...
(Идея задачи — gop2024)
Код — 39423501
Tutorial is loading...
Код решения I — 39423519
Код решения II — 39418926. Попытайтесь оптимизировать :)
Спасибо tfg за идею и код решения III. Хорошая работа!
Код решения III — 39392321










In B, you could stop thinking after writing a * b = x * y. Since x, y <= 1e9, you could just brutforce all divisors of x * y (which is (divisor of x * divisor of y) ) and be happy with the same complexity.
It won't have the same complexity. complexity will be O(sqrt(x*y))
x <= y, so it will be O(sqrt(y)).
Since x is gcd, so instead of all values, simply check for(i=x; i*i<=(x*y); i+=x) {//code}. Time complexity for this is O(sqrt(y)). Maybe slightly higher constants due to (long long) multiplication, though negligible.
P.S. Actually we are only interested in solution of form i = K*x, where gcd(K,x)=1.
cool one!!
I solved it and got AC but I cannot understand your sol ...can you explain more?
No need to bruteforce divisors of x*y. Bruteforcing divisors of y is enough.
It's enough to just brute-force the divisors of y = LCM(a,b), since all the numbers we're seeking divide y.
Yep, and just to bolster this, if you check A002182 in the OEIS for 'highly composite numbers', those with the greatest number of divisors, and then follow this through to the list of such numbers and their number of divisors, you can find that 897612484786617600, with 103680 divisors is the number with the greatest number of divisors that is below 1018 (and 103680 is easily iterable over).
I did the same thing Accepted
We can also check a*b > 1e18 by 1.0*a*b > 1e18
Thanks, but no thanks.
Precision error still haunts me in every night.
Or just use two variables, one with long long products and one with long double product, we can check if long double >= 3e18 and long long > 2e18 :D
GCC has built-in functions for handling overflow. Solution that uses
__builtin_mul_overflow: 39392133хех, в задаче B находил за корень все делители (не только простые) числа y, их получалось немного (10^9 их было всего лишь 100). А потом за квадрат комбинировал все (проверял на l, r и другие нужные проверки на gcd, lcm). Хммм... Зашло. Повезло с тестами? http://codepaste.me/f804f38a <- код здесь
Их максимум 1344 у числа 735134400 (link 1, link 2), и это все равно бы зашло
Nice round, i liked the problems :). may i suggest that you change the problem statement of D slightly from "where p is the product of all integers on the given array" to "where p is the product of all integers in the selected sub-array". the example test cases do clear up the confusion though so it was fine
good problems E&D
but as a recommendation for authors, I think the test cases for E weren't strong enough(enough for square-root codes but not for others) since some o(n^2) solutions got ac(see my comment on advertisement blog)!!!
hope it'll never happen again!!!
ps:
my comment on advertisement blog :
http://codeforces.net/blog/entry/60050#comment-438494
You know, it’s impossible to catch everything since there are only few of us (authors and testers) against the entire community :)
Gotta try to add that test to upsolving.
Actually, authors aren't gods, they can't guess all possible wrong solutions and approaches that exists in the world and they can make mistakes too, so. I wouldn't complain much about that test case — won't be surprise if that guy will be the only one who will fail on it (curious about that, actually).
i 100% agree with you and :
i didn't want to complaint with anybody who helps, sorry if it looked like that ... :)
For the problem C, can anyone please elaborate how do we get the expected value of dresses at the end of a month?
If at some point you have X dresses, at the end of that month you may have 2X or 2X-1 dresses. If you draw that as a binary tree, and write down all possible numbers of dresses after K months, it's easy to see that they will represent a sequence of 2^k consequent numbers. More generally it will look like this: 2^k*x,2^k*x-1,2^k*x-2,..., 2^k*x-(2^k-1) Those are all possibilities for numbers of dresses. Summing them up you get, 2^k*x*2^k-(1 + 2 + ... + (2^k-1)) = 2^k*x*2^k-(2^k-1)*2^(k-1) Remember we need to double that value since the last month numbers of dresses only doubles, the wardrobe doesn't eat any. So the sum is 2^(k+1)*x*2^k-(2^k-1)*2^k. Now divide that with 2^k to get the arithmetic mean, you get 2^(k+1)*x-2^k + 1. It's all about writing it down.
this problem was actually easier than B xD
True that
I agree. If there were not some tricky test cases in C (like if x is a multiple of 10^9+7) actually people would do it more than B.
Can you explain why you divided on 2^k at the end?
The expected value of number of dresses is what we are looking for. Expected value is equivalent to arithmetic mean which we calculate by dividing sum of the numbers by how many numbers there are. ((a1+a2+...+an)/n). Therefore, having 2^k possibilities for number of dresses and their sum already calculated, we calculate the arithmetic mean like this: sum/2^k (sum = 2^(k+1)*x*2^k-2^(k-1)*2^k).
anyone please explain solution of problem D I am not getting it through editorials
First, we'll analyze this problem in an O(n^2) solution:
Initialize 2 arrays PrefSum[n] and PrefProd[n] in which PrefSum[i] is the sum of first i number in the array, and PrefProd[i] is the product of first i number in the array. After that, we count the subsegment by for loops.
Looking at this solution, we can easily notice that k*SumOfSegment cannot exceed 10^5*10^8*10^5=10^18, so that ProductOfSegment cannot exceed 10^18<2^60, which means a subsegment can never have 60 or more numbers that greater than 1.
With this fact, we can reduce the complexity of this solution to only O(n*60).
The trick here is you have to find the way to skip the 1's in the array using pre-calculated arrays, without leaving out any possible answer. When skipping each group of consecutive 1's, we can prove that there are only at most 1 possible answer between this group. That way, we can keep each loop in O(60) complexity.
Here's my code (C++14): https://ideone.com/JLNwsZ
Hi, the explanation you provided is very helpful. Why the PrefSum[n] and PrefProd[n]are storing the values for first i numbers? Shouldn't they be 2D arrays storing values for (i,j) implying sum and product from ith element to jth element if we want to consider all subsegment?
You could get sum of the subsegment from i to j by PrefSum[j]-PrefSum[i-1]. Same mechanism works for PrefProd. The prefix sum is very useful in reducing the memory and time complexity of your solution.
To initial the prefix sum array, you start with pref[1]:=A[1] then for each i:=2 to n: pref[i]:=pref[i-1]+A[i]
i did the same thing but i dont know why i am getting wa
http://codeforces.net/contest/992/submission/39416834 :(
Your failed test consists of n 1's. I think the problem is in the way you skip the 1's and add the subsegments to the answer. Try to debug on these kind of test!
Wouldn't PrefProd[i] overflow? How can we keep on multiplying array entries and storing in PrefProf[i]? Thanks.
That's just my very early O(n^2) approach for this problem so that I could show you how I reduce my complexity in this problem. I know that PrefProd[i] could overflow (it should be :)) ) but that doesn't really matter in my real solution.
Actually A can be solved in O(N) where N = 2e5 Just store all negative numbers as
where a[i] < 0.
Space is increased here but still better than N*log(N) on an average
Why does this idea not work for D?
For every array index which is 1 I store the number of 1s after that so that I can directly jump to the next index. (for example, 1 1 3 1 1 1 4 I get 2 1 — 3 2 1 -)
Now a normal nested for loop and if array[i] == 1 then if sum * k was less than prod and after adding no. of 1s following that 1 if sum * k >= prod, answer is incremented.
And normal check for prod == k*sum for elements other than 1.
Simplified Code
Can anyone explain the problem E to me? I have trouble understanding the query part? Particularly, We find the leftmost element which may be king-shaman yet. We can realise that it's the leftmost element, which doesn't lie in the good prefix (as there isn't king-shaman according the definition), which have a value at least . It can be done using segment tree with maximums, with descent. The left-most element that may be king is (i+1) ? And how is this O(logN) ? Thanks
can somebody tell me, in B why we are running the for loop from i = 1 to i^2 < (y/x)
We are looking for all divisors of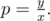 Of course, if j is a divisor of p, then so is
Of course, if j is a divisor of p, then so is  , and one of i or
, and one of i or  is less than or equal to
is less than or equal to 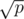 . So it suffices to iterate over the divisors of p which are less than or equal to its square root; the ones that are greater than or equal to the square root of p will automatically "show up" as
. So it suffices to iterate over the divisors of p which are less than or equal to its square root; the ones that are greater than or equal to the square root of p will automatically "show up" as  for some divisor
for some divisor 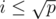 of p.
of p.
nice explanation , thanks
If somebody could tell me why my solution for D gives the wrong answer on Test 133, I would be very grateful.
I keep the positions of the nonzero elements in a vector, traverse this vector, while also keeping a track of the number of ones to the left and the right of the current subsegment we're considering.
Got it — overflow on finding the product was the problem. AC now!
In Problem E Solution 1,
We can realise that it's the leftmost element, which doesn't lie in the good prefix (as there isn't king-shaman according the definition), which have a value at least p[i]. It can be done using segment tree with maximums, with descent.How can we find this index in log(N)?
I could only think of (log(n))^2 approach.
Do a maximum query segment tree. When you visit the segments that cover the range, if the maximum element is what you need you go down else just return n. Now, you are in a range that has the answer you need, you just need to decide wether to go left/right. If the maximum element to the left if what you need, go left otherwise go right.
I'm still no clear. Could you please explain a little bit more?
Here is a snippet of code from solution1:
The
getmethod is to find the leftmost element which is larger than value S. And if we ignore thedownmethod called in it, I think the time complexity of it is the same asget_sumsince in the worst case theresis n every time and it will call itself twice every time. And now we takedowninto account. Thedownmethod is log(N) itself. So the time complexity of the method should be log(N)^2. How can we tell that the complexity ofgetis log(N)?get() visits the "cover" of the range, so the same segments that something like get_sum() would visit. Once it gets to a range that it calls down, it will get an index and will go back returning it (if there's no answer there, it won't call down). So the first part (visiting the ranges that cover the query range) is O(log) and the second part (down) is O(log) too.
Oh I got it.
downwould be called once at most(ignoring recursive call). Thank you very much!In problem B , test 7 we have the input 1 1000000000 158260522 158260522, whose answer is 1. How can we have a number b/w 1 and 1000000000 whose hcf is greater than the number itself, shouldn`t the answer be 0.
1 and 1000000000 are the lower and upper bounds of the two numbers. The HCF and LCM both have to be 158260522.
oh, i miscalculated the number of zeroes
Thanks for such a good contest. I like problems, they are interesting to me and especially I like 3rd solution of E problem.
Any sqrt decomposition solution for E passed?
I made one just now.
In problem B, Is There any efficient way to solve it if the "LCM" condition removed, I mean:
Given three numbers l r x , count number of pairs (a,b) such that l <= a,b <= r and GCD(a,b) = x.
where : (1 ≤ l ≤ r ≤ 10^9, 1 ≤ x ≤ 10^9).
Why complexity of problem A is nlogn we are just looping through the n elements then why not O(n) where did logn came from??
If you use a map or set to find how many different numbers there are, you have additional log(n) factor for mapping the values, though it can be done in O(n) using an array instead of those two mentioned above.
girlfriend !!!!
FFFFFFFF!!!
If you know the answer can you explain I am not getting this or I am missing something?
Here are my solutions to the problems of this contest.
I found problem E quite difficult to understand so I wrote an editorial here. This was for the first approach mentioned in the editorial with the maximum and sum segment tree.
I also loved the third solution presented to E so I provided by own exposition of this bitwise bucket method here.
can someone please explain how the grouping is done in the solution 3 of prob E?
Контест хороший, таски интересные
When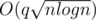 didn't pass but O(qlog2nlog(2e9)) does, you realize how fast binary search on fenwick trees really is! 39512053
didn't pass but O(qlog2nlog(2e9)) does, you realize how fast binary search on fenwick trees really is! 39512053
You can remove one logn if you use segment tree instead of binary search + BIT.
Thanks Foosball master!
In problem B c*x=a and d*x=y then he said that GCD(c,d) = 1!! is that a proof or this is a rule how should i had known!
c*x=a and d*x=b, if GCD(c,d)>1 then GCD(a,b)>x.
Can someone explain in solution I of 992E, what is meant by descent:
"We find the leftmost element which may be king-shaman yet. We can realise that it's the leftmost element, which doesn't lie in the good prefix (as there isn't king-shaman according the definition), which have a value at least . It can be done using segment tree with maximums, with descent."
Anyone getting WA on test #133? Couldn't identify the problem. My WA submission.