__noob__'s blog

Sum of xor over all the triplets.
By __noob__, history, 6 years ago, In English

Given an array of N integers and Q queries. For each query you are given two integers L and R(where L<=R<=N) you have to output the sum of xor over all the triplet i,j and k where L<=i<j<k<=R Constraints 1 <= N <=10^5 1 <= Q <=10^5 1 <= A[i] <=10^12

Can anybody help me out on how to solve this question?

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (8)
| Write comment?
»
6 years ago, # |
  Vote: I like it +14 Vote: I do not like it

The main observation is that the XOR is independent over all bits. Then lets have a partial sums array over all bits. This way in O(1) we can find the number of k-th bits set in a range.

Well then for each query in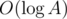 we can find the answer by simply considering each bit (when you have the number of 1's and 0's in the range at the given bit, you can calculate the value for that bit in O(1)).

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Can you please explain a little bit more.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well imagine the rangle [L; R] has three numbers {3, 2, 16}. Then their 0-th bit xor is 1, 1-st bit xor is 0, 2-nd bit xor is 0, 3-rd bit xor is also 0 and 4-th bit xor is 1. Well then we simply can add 20, 21 and 24 to the answer. This is what I meant by "the xor is independent over all bits".

      The algorithm will look like that for each query:

      1. Consider i-th bit.

      2. Count the answer if all numbers with 1 on this bits are ones and all over are zeroes. Let the answer be S.

      3. Add S * 2i to the answer.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let's assume we are calculating the answer for bit B in the range [L, R].

      Three numbers (i, j, k) will ⊕ (bitwise XOR) to 1 if (i = 1, j = 0, k = 0) or (i = 1, j = 1, k = 1) (obviously including permutations of (i, j, k)).

      Let x be the count of 1s in the range [L, R], and y be the count of 0s in the range [L, R]. We have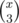 ways to pick three 1s out of this range, and ways to pick a 1 and two 0s. Therefore, the answer is 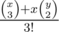(we divide by 3! because we are only looking for unordered triplets).

      → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

First find prefix sum for each bit. This way we can find number of elements in range l to r which have ith bit set( i from 0 to ceil(log10^12)). Now say in range l to r there are k elements which have ith bit set. Then if we take 3 elements from them then they will contribute value of ith bit to xor sum. So add to xor sum kC3*ith value. And if we take 1 such element and 2 elements which don't have that bit set then also their triplet will contribute value to sum. k*((r-l+1)-kC2)*value

→ Reply
»
5 years ago, # |
  Vote: I like it +5 Vote: I do not like it

https://www.hackerearth.com/practice/data-structures/advanced-data-structures/segment-trees/practice-problems/algorithm/xor-sum-1-af648068/ editorial would help :p

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

nice question

→ Reply