Hi Coders,
I am trying to solve a problem but couldn't come up with a better solution.
Problem Statement
Given an array A of N integers and Q queries where 1 ≤ Ai ≤ 100, 1 ≤ N ≤ 105 & 1 ≤ Q ≤ 105. Each query gives L and R(a subarray of array A). For each query find the minimum X such that AX > AL + X - 1 and L + X - 1 ≤ R.
I tried solving this problem but couldn't come up with a solution better than Q × N. Any help to improve the complexity would be much appreciated.











So, you need to find the leftmost element in the subarray which is greater than the element at the beginning of the subarray. I think, you can use some preprocessing. Make a
setstoring pairs of elements with indices —pair<int, int>, where first element is the index and the second is the value. Then, for answering the queries you just dolower_bound(setOfPairs.begin(), setOfPairs.end(), make_pair(L, A[L])), which will give you the answer. The resulting complexity is O((N + Q)logN).The question asks for the minimum X such that AX > AL + X, not AL > AL + X.
My bad.
However, I am unable to analyze the complexity of the final step. The total complexity is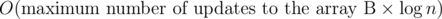 .
.
Yes, i understand your solution correctly and its better but in the worst case, its gonna be N*Q*log(N). It wont help much :(
lol
Thanks for the comment but looks like either you got the problem wrong or i did not get your solution right
lol
Assume array {4, 6, 7, 5, 7, 5} and a query [4,6] (1 based indexing) then the answer is 3 right ? Will your solution work here ? And if yes, can you please elaborate your approach more ?
lol
Can you tell me how your solution will work ?
lol
Assume array {5, 6, 5, 5, 7, 4} and a query [4,6] (1 based indexing) then the answer is 3 right ? And ur above hypothesis wont work here.
Ai = Aj and i < j but still j is the answer in above case
lol ok my bad
Can you give an example testcase with Q > 100?
Is this problem present in an online judge? If yes could you give us the link?
No it's not. This problem was given in assignment for slightly lower constraints N,Q <= 5000
why do you think that the task has a quick solution?
Thats what i am trying to figure out.
Fft?
Bitset can help:
For each position i of the array, maintain a bitset bits[i] which will contain 1 for the L s that have answer ≤ i.Then you can binary search the answer for each query in log(n) time.
To build the bitset,sort the array in increasing order. In case of a tie, keep the earlier element earlier. Now, iterate over the sorted array. Maintain a global bitset globalbits. If you are on a element which was at i th position in the original array, then make bits[i] = globalbits > > i. Now bits[i] contains 1 for all the L s which have an answer i(maybe better answer exists).Then make the i th position of globalbits 1. Do this for the whole sorted array. To obtain the final bitset, iterate from 1 to n and make bits[i]| = bits[i - 1].
Memory complexity: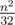
Time complexity: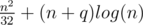
Hey everyone,
I know how to do in O(N*|A[i]|+N*logN) preprocessing with O(1) per query.
First, notice that since the problem asks for X minimum, the R bound is simply irrelevant: You just select the minimum X for some L, and then finally just check if also L+X-1 <= R. Now, given that each query is actually a number between 1 and N, we will preprocess all queries as follows.
For each possible VALUE v of the A-vector (at most 100 of them), keep a linked list of increasing indexes j who have A[j]==v. The total number of elements in all lists will be N.
Then loop from the left (from 1) up to N with a candidate Ax and determine for which elements that A[x] is actually the optimal answer. For each candidate A[x]==w, do the following in all the (at most 100) lists of smaller elements: find the element with the smallest index >=x in that list (since x is increasing from 1 to N, you can just keep track of "the last position visited" for each list, so you don't have to walk them from start at each candidate x). All indexes in the list at or beyond that one, could be the A[L+x-1] of the answer for some adequate L (each one for a different L). The adequate L's for each index j in the list, will be j-x+1. So if the answer Ans[j-x+1] was not already filled out before, it will be that value. Taking this approach directly, results in an O(n^2) preprocessing. To reduce it, we need to visit each element in one of the 100 lists only when it is actually used as an optimal answer for some L. Notice that as we move with x from 1 to N, the potential L for which x is the answer, for each index in the lists increases also by 1 at each step. So, both the intermediate lists and the lists of unsolved L's (from which Ls are cut off) remain sorted from one execution to the next (only their values change). This becomes a well known problem called "Fast Set Intersection" in memory. See https://arxiv.org/abs/1103.2409 and https://link.springer.com/chapter/10.1007/978-3-540-27801-6_30 for some ideas on this.
To circumvent issues with dynamic set intersection, you could, instead of walking with increasing x's, to also combine this into pairs (v, x) — that is also walk, increasingly, in terms of target A[L+x-1]=v value.
Then you could walk the entire vector A[] of values > v and simply, for each x (in increasing order), check in the list of L's with Ans[L]>x, the smallest one (the smallest L) greater than x, which has a value v after it. If you find one such — you walk all of them and adequately decrease there Ans[L] values to x. Note that one such eliminated at a step (v,x) will never show up again at any (v,x+alpha) steps (since its Ans[L] will be <x+alpha). Using a simple AVL Tree, you could do this in O(log n) per (v,x) pair plus the time to potentially update Ans[L]'s (which is at most O(n) for a (v,*) run, thus O(n*|A[i]|) in total). However, given that the x increases monotonically for each (v,*) run, you can loose the AVL tree, and simply have the Ans[] vector elements in a sorted list, to be walked in non-decreasing order.
After doing the above for all (v,*) runs (thus for all (v,x) pairs), the final Ans[] vector will give the solution. Each run takes O(n) for the actual run, plus O(sorting(n)) to set up (which is at most O(n*logn)). I am also pretty sure the log(n) factor from intermediate steps could be cut out by some smart updating of the sort order. But still. To answer the original queries, you can just do a lookup the answer in this vector in O(1), and check if L+Ans[L]-1 <=R [otherwise the answer is Not Found].
Best, Mircea (sAca) 08.March.2020 @ 22:29 laptop time, Nizhny Novgorod.