icpc_expert's blog

Binary Search
By icpc_expert, history, 6 years ago, In English

I want to know how to binary search on answer where the function is first decreasing attains its minimum and then again function starts increasing.

  • Vote: I like it
  • -5
  • Vote: I do not like it

Comments Comments (16)
| Write comment?
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Keep l and r variables as usual. For your m=(l+r)/2 (the value you actually test), you should test both m and m+1. If the function is decreasing, you are still in the left half. If it is increasing, you are in the right half. You want to find the earliest point in the right half. So it would be something like:

int l = 0, r = MAX;
while(l < r) {
    int m = (l+r)/2;
    if(f(m) < f(m+1)) r = m;
    else l = m+1;
}
// l and r will both be the desired value

You have to be careful of the case where it is strictly decreasing/strictly increasing the entire time. I didn't check it carefully above.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I was doing the same thing but still if l==r then what your function will do also can you please code for me the question that I was trying to do. The ques is you are given an array of size n you have to return the index of position at which you will cut the array such that the difference b/w the sum of 2 parts obtained after cutting is minimum.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      If l == r you are done, l and r will both contain the number you are looking for. Thinking it over, I actually think the code above might just be correct even for edge cases.

      I'm not going to code that question for you, but I'll let you know that you can try each index in O(1) if you calculate prefix sums beforehand and then take O(n) to try all indices.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In some problems, I have seen people code binary search with the condition l <= r, but never understood why they did that. Do you have an idea about that approach ?

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          To be completely honest, I know for a fact that I have done this before as well, but I have no idea why. Every time I do binary search, I just think about what is appropriate on the fly and think about the edge cases. I know this probably isn't the response you were hoping for, but I really can't think of a reason to do l <= r despite the fact that I've done it before.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            Well thanks anyways. Maybe I'll try to ask someone after a live contest, when I see such a submission for any problem.

            → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

why so many downvotes??

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Here's another way of approaching the problem (that I find easier to understand than messing with while loops). Suppose your function/array looks like this: xxxxxxoooooo, and you want to find the last x. Let your current answer be i=0. Since every number can be represented in binary, you can start with some large value of k and see if f(i + 2^k) is still an x. If it is, then i += 2^k. Keep doing this for all k->0, and at the end, i should have the value of the last x.

You can think about this way as starting with the binary number 00000, and then adding 1's from left to right to get something like 10110, the number in binary.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Google "ternary search"

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you pls help me in knowing the difference b/w binary search and ternary search I am talking about what kind of problems are solved with ternary search that can't be solved with binary search.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In general, binary search is applicable if your check function is monotonic, i.e, for all pairs (x, y) such that x < y, you have f(x) ≤ f(y) or f(x) ≥ f(y).

      Ternary search is applicable if your check function has a maximum (or minimum) value somewhere, and is strictly monotonic on both sides of this critical point. For example, the general graph of a quadratic equation — f(x) = ax2 + bx + c, a ≠ 0, and the graph of f(x) = |x| look like this.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I think all problems that can be solved with ternary search can also be solved with binary search by searching on the derivative of that function. As if function is like this ////_\\\, then its slope will be ++++++0-----. We just have to search for point zero!

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Not all, no. Most of the time it should be possible, I agree. However, there are at least two cases which I can think of where it doesn't work.

          1. When you can't calculate the derivative of the function — not as uncommon as it may seem, since we deal a lot with discrete functions rather than continuous ones, and extrapolation isn't always going to work. Even if the function is continuous, there's a much higher chance of it not being differentiable anywhere than of it being differentiable at even a single point!See this.

          2. If the function in question has a saddle point, the derivative there is zero, but the function does not have an extremum there.

          In simple terms, your derivative might be something like +++0+++0---0---. In that case, binary search will fail, but ternary search will still give you an answer.

          Edit: Saddle point, not point of inflection. My bad.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            If the derivative is +++0+++0---0--- , We can find the zero with + on the left side and — on the right easily. I forgot to write which 0 are we finding out in my previous comment.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              No, my point was that there could be 0s mixed into the derivative at random spots. You usually aren't going to know that they are there to ignore them, and the function is no longer monotone, so binary search isn't going to work on it to find the one single 0 which lies between a + and a -. Ternary search won't have this problem.

              For a more concrete example, look at this function: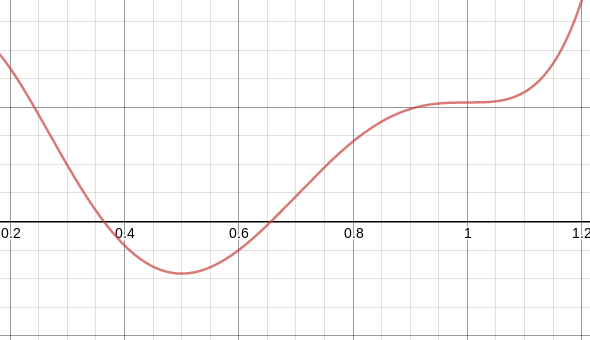

              The derivative is 0 at both 1 and 0.5, but 1 is not an extremum. What is to say that binary search will find 0.5 (the actual answer) and not 1?

              → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Binary search is finding x such that f (x) is closest to v (v is value you want to find)

Ternary search is finding x such that f'(x) is closest to 0. Derivative is not defined but you i think you can understand what i mean..

→ Reply