255A - Тренировки Егора
Идейной сложности задача не представляла. Просто посчитаем суммы по всем группам мышц и выведем ту, сумма у которой самая большая.
255B - Разбор кода
После применения 1го вида операций все буквы "х" выйдут на начало, а "у" вконец. После применения операций 2го вида, останутся только буквы, которых больше. При чем их количество это модуль разницы количества букв "х" и "у".
256A - Почти арифметическая прогрессия
Заметим, что ответ это длина последовательности: a, b, a, b, ... где a и b — некоторые целые числа. Зафиксируем одно число (допустим a), будем перебирать число b, и считать какой мы получим ответ, если это будет последнее число в последовательности. Заметим, что для фиксированных a, b — ответ считается жадно. Так же будем действовать и тут. Будем искать последнее вхождение числа b до зафиксированного, что между ними есть число a, и будем брать ответ как длина до найденного числа +2 (икасть будем с помощью метода двух указателей). Так же нужно рассмотреть случай, когда это будет 1е или 2е вхождение в последовательность.
Так же существует решение с помощью динамического программирования.
Асимптотика обоих решений O(n^2).
Буду очень рад, если кто то напишет решение с лучшей асимптотикой.
256B - Остап и квадрат
Существует несколько решений этой задачи. Мое решение — это бинарный поиск по ответу. Дальше нужно посчитать площадь усеченного квадрата, повернутого на 45 градусов. Это можно сделать так: посчитаем его общую площадь. Отнимем то, что отсекает верхняя часть. Аналогично для нижней, левой и правой. Добавим то, что отсекают углы. Можно написать функцию которая по длине усечения считает нужную площадь, для того что бы не писать много кода.
256C - Фурло и Рубло и Игра
Заметим, что после первого хода любая кучка превратится в кучку размера не большего чем 1000000. Будем считать функцию Гранди для чисел меньше 1000000. Функция Гранди очень маленькая, по этому можно заводить частичные суммы для каждого вида Функции, что бы быстро говорить какие функции есть на отрезке, а каких нету. Зная ответы для маленьких не сложно посчитать ответ для всех кучек.
256D - Вруны и Сережа
Если человек говорит число x, и в общем число x сказало x человек, то мы не можем сказать: врет этот человек или нет.
Теперь понятно, какие последовательности нам подходят. Будем считать их с помощью динамики: dp[n][m][k], n — какие ответы мы сейчас рассматриваем, m — сколько человек уже сказали свой ответ, k — сколько среди поставленных точно врут.
Переход:
dp[n][m][k]*cnk[N-m][n] -> dp[n+1][m+n][k]
dp[n][m][k]*cnk[N-m][p] -> dp[n+1][m+p][k+p] p = 1 .. N, p != n.
Мы считаем, что N — количество людей всего. Такая ДП не укладывается по времени, по этому нужно завести массив констант. Так как N — степень двойки, массив выйдет не большой.
256E - Счастливые массивы
Решение задачи — дерево отрезков. Будем хранить в вершине динамику f[i,j] — какое количество способов заменит нули на отрезке который соответствует вершине, что в начале отрезка будет число i, а в конце j.
При нормальной реализации данный подход без проблем заходит по времени.











Можете поподробнее расписать в задаче 256B - Остап и квадрат про подсчет площади усеченного квадрата и особенно про функцию которая считает отсечения?
И про динамику в задаче C.
Пусть а[] — массив входных чисел. Пусть dp[i][j] — длина длиннейшей почти арифметической подпоследовательности заканчивающейся в позиции i, у которой предпоследний элемент в массиве a[] на позиции j, причем j < i. Тогда, если существует k такое, что k < j & a[k] == a[i], то выберем среди всех удовлетворяющих ограничению k максимальное. В этом случае ясно, что dp[i][j] = dp[j][k] + 1. Причем k можно найти бинпоиском, т. е. для каждого числа x из исходного массива заведем вектор v[x], в котором будем хранить позиции на которых встретился x. Ясно, что, когда мы ищем k, нам надо просто найти максимальный элемент k из v[a[i]], такой, что k < j. Если же k удовлетворяющего условию не нашлось, то нет предыдущей подпоследовательности которую можно расширить, тогда положим dp[i][j] = 2.
Остался один нюанс, мы умеем находить длины последовательностей, которые больше либо равны 2. Но если во входе всего один элемент, то надо вывести 1.
В результате время работы равно O(n^2 log n)
Спасибо за понятное объяснение
1) "если существует k такое, что k < j & a[k] == a[j]" — наверное, имелось ввиду "если существует k такое, что k < j & a[k] == a[i]"
2) Кажется, не у всех людей заходило n2log(n), можно было находить очередное k за O(1), сделав предподсчет
1) да конечно), поправил
2) если сделать map из чисел массива в vector индексов, тогда проходит по времени за 0,5 сек
Задача С div 2/A div 1: почему на тест 5 4 4 3 5 1 ответ 2 (3-ий тест)? Мы можем взять, например, последовательность 4 3 4, т.е. ответ = 3.
Мы не можем взять такую последовательность, т.к. числа в массиве идут не в этом порядке. Прочитайте, что написано в условии про подпоследовательность.
Спасибо
Задача С div 2, почему на тест 2 3 2 2 1 3 ответ 4?
Потому что ответ — это 2 3 2 3, а это четыре числа))
3 2 3 2.) последовательность замкнутая .
Can you translate tutorial for Div2 C also, please? Or if someone else could give a detailed explanation I would be thankful :)
One solution that pass system test.
Note that the task actually asks about the longest subsequence in the form a, b, a, b, a, b, ..., and we can do the following.
First normalize the elements into ranks when they are sorted. e.g.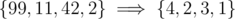 . Then define a function fi, r be the longest subsequence obtained ending at the i-th element, and the previous element is of rank r. Define fi, 0 = 1 for all i, being the base case. Then one can derive the following transition:
. Then define a function fi, r be the longest subsequence obtained ending at the i-th element, and the previous element is of rank r. Define fi, 0 = 1 for all i, being the base case. Then one can derive the following transition:
where rj is the rank of the j-th element. Since there are O(n) different ranks, using DP the algorithm takes O(n2) time to compute all fi, r. Pick the largest among them as the answer.
A Detailed Explanation Indeed !
problem "256A — Almost Arithmetical Progression" is in Russian. Dose it have English editorial?
this is my idea :
define dp[i][j] = maximum length of subsequence of sequence of b that two first element of it would be equal to b_i and b_j
dp[0][0] = 1 and dp[i][j] = 1 + dp[j][k] (k is last element that is b_k is equal to b_i)
the only problem is to find k for every i and j that can be solved easy by make a vector for every b_i values of indexes for every b_i (1<=b_i<=1000000) and binary search ...
code : 2785803
DP solution for 256A
В Div 1 D сплошной прекалк, а не нормальные решения.
Чем объясняется, что в задаче C div 1 функция Гранди мала?
Можно найти ее для чисел порядка миллиона, заметить что она маленькая. Для чисел порядка 10 в 12й будет не более чем на 1 больше.
В задаче 256C - Фурло и Рубло и Игра не совсем понял, что делать, если размер кучки больше, чем 106. Подскажите, пожалуйста. То есть ясно, что после того, как из нее первый раз возьмут камни, ее размер станет меньше, чем 106, но я не понимаю, что это дает.
Это дает то, что можно сделать precalc значений функций Гранди от 0 до 10^6. И использовать эти значения для вычисления функции Гранди уже для больших кучек.
Точно! Спасибо.
В С div.2 проходит и такое решение:
Для начала используем сжатие, после перебираем i = 1 до n-1 и j = i+1 до n, если a[i] не равен a[j], то d[a[i]][a[j]] = d[a[j]][a[i]] + 1. В получено массиве d возьмем максимум среди элементов как временный ответ ans, также значение аns увеличим на 1. После возьмем максимальное количество повторяющихся элементов в массиве a, и если это количество больше ans, то ans становится равен этому количеству. Ответ будет ans. Это решение у меня прошло, но я так и не понял доказательства. Кто сможет объясните.
Your tutorial is as well as your problems , tnx
Thanks for the editorial! However, could you please translate the explanation for problem C Div2 into English? Thank you.
Thought this might help
Translated version of Div2 Prob C:
Note that the answer is the length of the sequence: a, b, a, b, ... where a and b — integers. We fix one number (say a), will sort out the number of b, and consider what we get a response, if it is the last number in the sequence. Note that for fixed a, b - the answer is greedy. So are we going to act and there. We look for the last occurrence of b fixed to that between them is the number of a, and we will take the length of the response to the found number +2 (Ikast be using the two pointers). As it is necessary to consider the case when it is 1st or 2nd occurrence in sequence.
There is also a solution using dynamic programming.
Asymptotics of both solutions O (n ^ 2).
I would be very happy if someone would write a better solution with asymptotics.
Credits: translate.google.com
A "brute-force" solution for 256A — Almost Arithmetical Progression.
The problem asks to compute the length of the longest subsequence in the form of a, b, a, b, ....
Let A[1..n] denote the origin array. One easy observation is that the value of each A[i] is not important, and thus, we can map each A[i] to the range [1, n] accordingly. Let pos[i] contain all indices of number i in A. For example, A = [3, 2, 2, 1, 3, 2], then pos[1] = [4], pos[2] = [2, 3, 6], pos[3] = [1, 5].
If a = b in the optimal subsequence, the answer is just max(pos[i].length). Otherwise, we enumerate all pairs of (a, b), where a ≠ b, and computing the longest subsequence, when both a and b are fixed, can be done efficiently by merge-sort. (Note that, all pos[i]'s are already in sorted order.) It then remains to analyze the total runtime of this procedure. There are at most n unique keys for pos[i], so O(n2) time for enumerating all pairs of a, b. Plus all the mergesorts, it seems like the overall runtime is O(n3). Fortunately, it is not the case, and a tighter bound is O(n2). Why?
If we do a more careful analysis, the total runtime is bound by
Therefore, the problem can be solved by brute-force in O(n2) time using linear space.
Suppose there are k unique values.
for i = 1 to k
for j = 1 to k calculate(i, j) => this should be done in |b(i)| + |b(j)| operations using two pointersthen for j loop, total operations would be
|b(i)| + |b(1)|
|b(i)| + |b(2)|
.
.
|b(i)| + |b(k)|
so total would be k * |b(i)| + n (right column sums to total values n)
now doing similar for the outer loop
k*|b(1)| + n
k*|b(2)| + n
.
.
. k*|b(n)| + n
Adding all columns, total operations would be k * n + n * k = 2 * n * k = O(nk) where k is the total number of unique values. since k <= n this O(n^2) is achieved
Nice analysis.
DP Solution for 256A
As others have already pointed out, you can map A[1..n] values to 0..n-1
Once, the values are mapped, fill an array dp[i][j] which contains the max subsequence length ending with i and previous element being j.
21394975 is my Accepted code
I tried really hard to implement this DP with a top-down recursive function, but I failed... Can you please help me with that? Thanks!
Here you go 23015907 :)
Needed to do some additional preprocessing to get it within timelimit.
Do you think it's possible to achieve n^2 with a recursive solution? This situation is really impressive to me... I thought that all bottom-up DPs had a top-down version with at least the same time complexity... Knapsack/Bellman-Ford/Floyd-Warshall are all DPs that need more space when implemented recursively, but they have the same time complexity! =(
I'm not really sure. There might be a n^2 solution but I'm unable to think of one.
Also, it is worth noting that none of the top 30 div-1 folks used Top-Down approach. I read people are generally worried about stack-overflow due to too many function calls. Check pros and cons section in http://stackoverflow.com/a/6165124
A detailed DP Approach for 256A
I found the editorial and and other comments' quite complex. I tried to explain the same approach in a bit simple way.
We have to find the longest subsequence of A,B,A,B,A,B,... Type. Since in an array of size n, we cant have more than n different numbers, we map the numbers accordingly. For example, a = [ 10 , 20 , 30 , 20 , 30 ] --> a = [ 0 , 1 , 2 , 1 , 2 ] We updated the initial array!
Now we create dp[n][n], where dp[ i ][ j ] means length of longest subsequence ending at i th element (a[ i ]) and j th element (a[j]) being the previous element in subsequence! Here's the tricky part: For every (i,j) , we dont update dp[ i ][ j ], Instead we update dp[ i ][ a[ j ] ]. (Yes, some dp[ i ][ j ] may never be updated , if array elements repeat , but we just have to find the maximum length. It'll make sense soon! )
Initialize: dp[ i ][ j ]=1 for all i,j possible.
Consider the following example.
a = [ 10 , 20 , 30 , 20 , 30 ] . We Updated it to -> a = [ 0 , 1 , 2 , 1 , 2 ]
DP Table would look like:
(0 based indexing). Array a=[0,1,2,1,2]
See the cases when i=4,j=1 And when i=4,j=3.
In DP Table Creation:
When i=4,j=1: dp[4][1] = max( 1 + dp[1][2] , dp[4][2] ) = max(1+1,1) = 2
When i=4,j=3: dp[4][1] = max( 1 + dp[3][2] , dp[4][2] ) = max(1+3,2) = 4
Observe:
See when i=4 , j=1 it means last element of sequence is "2" and 2nd last element of sequence is "1" , where "2" is the 4th element of a[] and "1" is 1st element of a[].
And when i=4 , j=3 it means last element of sequence is "2" and 2nd last element of sequence is "1" , where "2" is the 4th element of a[] and "1" is 3rd element of a[].
In both these above cases we updated dp[4][1] only. We never update dp[4][3].
dp[4][1] is Our answer means sequence is max. when it ends at 4th element and the value at 1st element is same as the 2nd last sequence element, but it not necessary that 1st element only is the 2nd last element in sequence !
There is a tricky difference here. Observe that 1st element is not the 2nd last element in sequence. But the value of 1st element is the 2nd last element in sequence, is what is defined by dp[4][1] !
My Code
This was truely one of the most beautiful DP Question! (And I feel worth 1800 maybe?! )
Edit: got it.
Can anyone please help me with this submission of 256A? I can't figure out what's wrong with it. https://codeforces.net/contest/255/submission/83326327
UPD: found the error (Sorry).
Div 2 Problem C LINK
i know i am late.
but i could not understand why i am getting wrong ans on test case 22.
help is very much appreciated
my code
idk if you still need any help but try testing for this test case: 4 1 1 1 1 if you get 1 as ans then it's wrong, the answer should be 4.
since p can also be zero.