Блог пользователя TooGoodToLoose

Why do we sort the left pointer by sqrt(N) in Mo's Algorithm?
Автор TooGoodToLoose, история, 6 лет назад, По-английски

In Mo's Algorithm, we sort the left pointer by using sqrt(N).

However if we consider two left pointers a and b such that a<b then (a/c)<(b/c) where c=sqrt(N). Thus it won't matter if we sort it by a<b or (a/c)<(b/c).

I know I am missing something, but I can't figure it out.

  • Проголосовать: нравится
  • -11
  • Проголосовать: не нравится

»
6 лет назад, # |
← Rev. 2   Проголосовать: нравится +1 Проголосовать: не нравится

In Mo's, if we have (a / c) =  = (b / c) then we sort queries on the basis of the right pointer, in which it is possible that some query [l1, r1] will come after [l2, r2] even when l1 < l2.

While sorting it just on the basis of the left pointer will not ensure us O(sqrt(N)) time complexity.

→ Ответить
»
6 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

I have no idea what you are talking about. In Mo's algorithm we categorize based on left pointers (put in sqrt bucket) then sort by right pointers. Converesly, it is possible to categorize on right pointers and sort by left pointer but that's weird so I don't see an obvious reason to do so.

We never categorize by left/right pointer AND sort by the same pointer (there would be no point in doing so).

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится +36 Проголосовать: не нравится

If you have an apple, then you have a fruit. But if you have a fruit, you don't necessarily have an apple.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

What you are missing is that (a/c) is actually floor(a/c), so a<b does not imply (a/c)<(b/c). Try a = 5, b = 6, c = 4

To understand Mo's algorithm, see LanceTheDragonTrainer's reply.

→ Ответить
»
6 лет назад, # |
← Rev. 3   Проголосовать: нравится +8 Проголосовать: не нравится

Sorting by (a/c)<(b/c) is splitting the array to blocks of size c and sorting by which block the left pointer is in. Let's analyze running time according to c, n, q (n/c blocks of size c):

  • The left pointer moves, in every query, either inside a block or to some next block. While moving inside a block, the worst case is between its ends, which is O(c) moves. In the worst case it will also move over all blocks in all queries, so that's O(n). We get its work to be O(cq + n).
  • The right pointer moves always to the right, unless our left pointer moves a block, which allows the right pointer to move all the way left (and then it can return right again). On worstcase, for each block it does O(n), which gives .

We want to minimize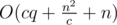 according to c. Choosing 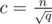we get 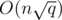while choosing 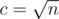we get 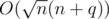. Even though the first one is always faster (according to math, but while ignoring the small change in constant), they probably have no difference in practice, especially when n = q (but the more they differ, the better the first one is in comparison to the second one).

Notice that by the formula, sorting by a < b is having c = 1, which has a complexity O(n2) worstcase.

→ Ответить