gXa's blog

Expected Value (Interview Question)
By gXa, history, 6 years ago, In English

A square grid(NxN) is given to you; Each location on the grid is either a brick (B) or its empty (_).

The total number of bricks is exactly equal to as much is required to build a “wall” in the grid. See example for clearer understanding.

That is, at the end , all bricks(B) should be placed at boundary locations.

For moving a brick from location <x,y> to <i,j> |i-x| + |j-y| fuel is used.

Each brick in the grid can be moved to any location on the boundary with equal probability. What is the expected value of the fuel required to do so? Each brick can be moved at-most once.

In the end (after moving all the bricks), the grid should look like:

 B B B B
 B _ _ B
 B _ _ B
 B B B B
  • Vote: I like it
  • +9
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
6 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Can we use linearity of expectation and just say the expected cost of a particular brick is the mean distance to all boundary points and the expected value of the total the sum of these values over all bricks?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yes, it is a correct solution.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Thanks for clarifying. Linearity of expectation tends to worry me because it often makes the solution seem too simple and I wonder am I missing something.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        There's a way to realize the solution in a straightforward way:

        Let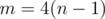 — number of bricks.

        The answer is: .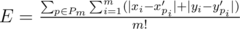

        (xi, yi) — original bricks. (x'i, y'i) — borders.

        If you consider some brick and some border position, it's simple to calculate a coefficient of manhattan distance in abovementioned sum. It is (m - 1)!.

        Thus we get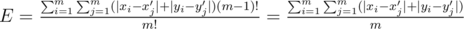 . Evidently, it is sum of average distances for all bricks.

        → Reply