Here is a problem I encountered during the Barcelona Bootcamp named 'Matrix Coloring':
Let F(n, m, k) be the number of ways to color the grid with n rows and m columns into k colors, such that any two neighbouring cells have different colors. We need to calculate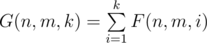 
modulo 109 + 7 under the constraints n × m ≤ 50, k ≤ 109.The time limit is 5 seconds.
The official solution involves DP on broken files and hardcode, which the latter part doesn't get me much satisfied. So, can any one offer some different ideas?
Actually, I'm kind of having some of problems dealing with these kinds of matrix coloring problems. Some restrict that the neighbouring cells should have different colors, while some restrict that no column/row should contain the same color, what's the general idea behind this kind of problems? If you know something, please share. Thanks!
The official solution is as follows. It can be observed(How? I'm a bit confused.) that for fixed n and m the answer is a polynomial in k of degree ≤ nm + 1. So we can use dp on broken files to calculate the answer for k up to nm + 1, and then use interpolation to find out the answer for large k, since this may not fit into the time limit, we should hardcode the coefficients.
About the answer polynomially depending on k: consider the following numbers: A(n, m, i) for 1 ≤ i ≤ nm: the number of valid colorings in i colors such that every color is used at least once. Then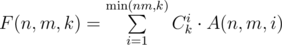
(here we iterate over the number i of colors that will actually appear in the coloring; then you need to choose i colors from k (Cik ways) and color the grid in i colors that were chosen (A(n, m, i) ways by definition of A(n, m, i)). Now,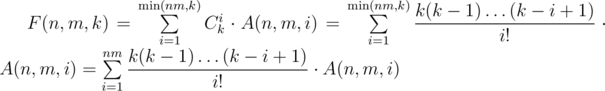 
(the last equation is true because k < i implies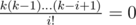
, so all summands with i > k are actually equal to zero). Now, the last sum is clearly a polynomial in k of degree not more than nm (A(n, m, i) don't depend on k in any way and each 
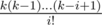is a polynomial in k of degree not more than i ≤ nm.
So, F is a polynomial in k of degree ≤ nm. Due to being the prefix sum of F, G(n, m, k) is a polynomial in k of degree ≤ nm + 1.
UPD Also, precalculating the coefficients seems to be really unnecessary: we need to run evaluation of F(n, m, x) at most nm + 1 times, each evalution can be done in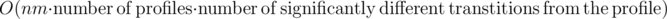
. Consider the n (we assume that n ≤ m, so n ≤ 7) cells that are currently on the 4-border of processed part of the grid. Only the partition of them into sets of the same color matters. Moreover, adjacent cells from the border should be of different colors. The number of profiles like that is pretty small (in the worst case of n = 7 there will be at most 255 valid profiles for any cell). Moreover, all transitions that use color that is not present in the current profile lead to the same new profile and therefore are not fundamentally different and can be counted at the same time. In the end, we call dp that does ≈ 50·255·7 operations about 50 times — that should fit the TL very easily even without any precalc. Am I missing something?
That solves the problem. Thankss!