Разбор
Tutorial is loading...
Код
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int n, L, a;
int t[maxn], l[maxn];
int main(){
scanf("%d%d%d", &n, &L, &a);
for(int i = 0; i < n; i++){
scanf("%d%d", &t[i], &l[i]);
}
int start = 0;
int ans = 0;
for(int i = 0; i < n; i++){
ans += (t[i] - start)/a;
start = t[i] + l[i];
}
ans += (L - start)/a;
printf("%d", ans);
return 0;
}
Разбор
Tutorial is loading...
Код
#include<bits/stdc++.h>
using namespace std;
const int maxn = (int)1e3 + 3;
int n, m;
char a[maxn][maxn];
bool can[maxn][maxn];
vector<int> must_have[maxn][maxn];
inline bool inside(int x, int y){
return x >= 0 && y >= 0 && x < n && y < m;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
can[i][j] = true;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++){
do{
a[i][j] = getc(stdin);
}while(a[i][j] != '.' && a[i][j] != '#');
for(int dx = -1; dx <= 1; dx++)
for(int dy = -1; dy <= 1; dy++){
if(abs(dx) + abs(dy) == 0 || !inside(i + dx, j + dy))continue;
if(a[i][j] == '.')can[i + dx][j + dy] = false;
else if (i + dx != 0 && j + dy != 0 && i + dx != n - 1 && j + dy != m - 1)must_have[i][j].push_back((i + dx) * m + j + dy);
}
}
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++){
bool good = false;
if(a[i][j] == '.')continue;
for(int cand : must_have[i][j]){
int x = cand/m, y = cand%m;
good |= can[x][y];
}
if(!good){printf("NO"); return 0;}
}
printf("YES");
return 0;
}
1059C - Sequence Transformation
Разбор
Tutorial is loading...
Код
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 6;
int seq[maxn];
int ans[maxn];
int ptr = 0;
void solve(int n, int mul){
if(n == 1){ans[ptr++] = mul; return;}
if(n == 2){ans[ptr++] = mul; ans[ptr++] = mul * 2; return;}
if(n == 3){ans[ptr++] = mul; ans[ptr++] = mul; ans[ptr++] = mul * 3; return;}
for(int i = 0; i < n; i++)if(seq[i]&1)ans[ptr++] = mul;
for(int i = 0; i < n/2; i++)seq[i] = seq[2*i + 1]/2;
solve(n/2, mul * 2);
}
int main(){
int n;
scanf("%d", &n);
for(int i = 0; i < n; i++)seq[i] = i + 1;
solve(n, 1);
for(int i = 0; i < n; i++)printf("%d ", ans[i]);
return 0;
}
Разбор
Tutorial is loading...
Код
#include<bits/stdc++.h>
using namespace std;
typedef long double dbl;
const dbl eps = 1e-9;
inline bool gt(const dbl & x, const dbl & y){
return x > y + eps;
}
inline bool lt(const dbl & x, const dbl & y){
return y > x + eps;
}
inline dbl safe_sqrt(const dbl & D){
return D < 0 ? 0 : sqrt(D);
}
struct pt{
dbl x, y;
pt(){}
pt(dbl a, dbl b):x(a), y(b){}
};
const int N = 1e5 + 5;
const int STEPS = 150;
int n;
pt p[N];
inline bool can(dbl R){
dbl l = -1e16 - 1, r = 1e16 + 1;
for(int i = 0; i < n; i++){
dbl b = -2 * p[i].x;
dbl c = p[i].x * p[i].x + p[i].y * p[i].y - 2 * p[i].y * R;
dbl D = b * b - 4 * c;
if(lt(D, 0))
return false;
D = safe_sqrt(D);
dbl x1 = p[i].x - D/2, x2 = p[i].x + D/2;
l = max(l, x1);
r = min(r, x2);
}
return !gt(l, r);
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> n;
bool has_positive = false, has_negative = false;
for(int i = 0; i < n; i++){
int x, y;
cin >> x >> y;
p[i] = pt(x, y);
if(y > 0)has_positive = true;
else has_negative = true;
}
if(has_positive && has_negative){
cout << -1 << endl;
return 0;
}
if(has_negative){
for(int i = 0; i < n; i++)
p[i].y = -p[i].y;
}
dbl L = 0, R = 1e16;
std::function<dbl(dbl, dbl)> get_mid;
if(can(1)){
R = 1;
get_mid = [](dbl l, dbl r){return (l + r)/2.0;};
}
else{
L = 1;
get_mid = [](dbl l, dbl r){return sqrt(l * r);};
}
for(int step = 0; step < STEPS; step++){
dbl mid = get_mid(L, R);
if(can(mid))
R = mid;
else
L = mid;
}
cout.precision(16);
cout << fixed << get_mid(L, R) << endl;
}
Разбор
Tutorial is loading...
Код (первое решение)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const int lg = 20;
const ll inf = 1e18;
int n, L;
ll S;
ll t[4 * maxn];
ll t_add[4 * maxn];
int cid = 0;
int w[maxn];
vector<int> down[maxn];
ll sum[maxn];
int up[maxn];
int p[maxn][lg];
ll dp[maxn];
int id[maxn], rb[maxn];
ll dp_sum[maxn];
vector<int> rm[maxn];
inline ll get_sum(int v){
return v == -1 ? 0 : sum[v];
}
void preprocess(int v, int pr = -1){
sum[v] = get_sum(pr) + w[v];
p[v][0] = pr;
up[v] = v;
id[v] = rb[v] = cid++;
for(int i = 1; i < lg; i++)
p[v][i] = p[v][i - 1] == -1 ? -1 : p[p[v][i - 1]][i - 1];
int dist = L - 1;
for(int i = lg - 1; i >= 0; i--){
if(p[up[v]][i] == -1 || (1<<i) > dist)continue;
if(get_sum(v) - get_sum(p[up[v]][i]) + w[p[up[v]][i]] <= S){
dist -= 1<<i;
up[v] = p[up[v]][i];
}
}
rm[up[v]].push_back(v);
for(int u : down[v]){
preprocess(u, v);
rb[v] = max(rb[v], rb[u]);
}
}
inline void push(int v){
t[2*v] += t_add[v];
t[2*v + 1] += t_add[v];
t_add[2*v] += t_add[v];
t_add[2*v + 1] += t_add[v];
t_add[v] = 0;
}
void build_tree(int v, int l, int r){
t[v] = inf;
if(l == r)
return;
int mid = (l + r)/2;
build_tree(2*v, l, mid);
build_tree(2*v + 1, mid + 1, r);
}
ll get_tree(int v, int l, int r, int ul, int ur){
if(ul > ur)
return inf;
if(l == ul && r == ur)
return t[v];
push(v);
int mid = (l + r)/2;
return min(get_tree(2*v, l, mid, ul, min(ur, mid)), get_tree(2*v + 1, mid + 1, r, max(ul, mid + 1), ur));
}
void set_tree(int v, int l, int r, int pos, ll val){
if(l == r){
t[v] = val;
return;
}
push(v);
int mid = (l + r)/2;
if(pos <= mid)
set_tree(2*v, l, mid, pos, val);
else
set_tree(2*v + 1, mid + 1, r, pos, val);
t[v] = min(t[2*v], t[2*v + 1]);
}
void add_tree(int v, int l, int r, int ul, int ur, ll val){
if(ul > ur)return;
if(l == ul && r == ur){
t[v] += val;
t_add[v] += val;
return;
}
push(v);
int mid = (l + r)/2;
add_tree(2*v, l, mid, ul, min(ur, mid), val);
add_tree(2*v + 1, mid + 1, r, max(ul, mid + 1), ur, val);
t[v] = min(t[2*v], t[2*v + 1]);
}
inline void upd(int v){
dp[v] = 1 + get_tree(1, 0, n - 1, id[v], rb[v]);
}
inline void add(int v){
set_tree(1, 0, n - 1, id[v], 0);
add_tree(1, 0, n - 1, id[v], rb[v], dp_sum[v] - dp[v]);
}
inline void remove(int v){
set_tree(1, 0, n - 1, id[v], inf);
}
void solve(int v){
for(int u : down[v]){
solve(u);
dp_sum[v] += dp[u];
}
add(v);
dp[v] = maxn;
upd(v);
add_tree(1, 0, n - 1, id[v], rb[v], -dp[v]);
for(int u : rm[v])
remove(u);
}
int main(){
scanf("%d%d%lld", &n, &L, &S);
for(int i = 0; i < n; i++){
scanf("%d", &w[i]);
if(w[i] > S){printf("-1"); return 0;}
}
for(int i = 1; i < n; i++){
int j;
scanf("%d", &j);
down[--j].push_back(i);
}
preprocess(0);
build_tree(1, 0, n - 1);
solve(0);
printf("%lld", dp[0]);
}
Код (второе решение)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const int lg = 20;
const ll inf = 1e18;
int n, L;
ll S;
int w[maxn];
vector<int> down[maxn];
ll sum[maxn];
int up[maxn];
int h[maxn];
int p[maxn][lg];
int path[maxn];
inline ll get_sum(int v){
return v == -1 ? 0 : sum[v];
}
void preprocess(int v, int pr = -1){
sum[v] = get_sum(pr) + w[v];
p[v][0] = pr;
h[v] = pr == -1 ? 0 : (1 + h[pr]);
up[v] = v;
for(int i = 1; i < lg; i++)
p[v][i] = p[v][i - 1] == -1 ? -1 : p[p[v][i - 1]][i - 1];
int dist = L - 1;
for(int i = lg - 1; i >= 0; i--){
if(p[up[v]][i] == -1 || (1<<i) > dist)continue;
if(get_sum(v) - get_sum(p[up[v]][i]) + w[p[up[v]][i]] <= S){
dist -= 1<<i;
up[v] = p[up[v]][i];
}
}
for(int u : down[v]){
preprocess(u, v);
}
}
int solve(int v){
int ans = 0;
int best = -1;
for(int u : down[v]){
ans += solve(u);
if(path[u] == u)continue;
if(best == -1 || h[best] > h[path[u]])
best = path[u];
}
if(best == -1){
best = up[v];
++ans;
}
path[v] = best;
return ans;
}
int main(){
scanf("%d%d%lld", &n, &L, &S);
for(int i = 0; i < n; i++){
scanf("%d", &w[i]);
if(w[i] > S){printf("-1"); return 0;}
}
for(int i = 1; i < n; i++){
int j;
scanf("%d", &j);
down[--j].push_back(i);
}
preprocess(0);
printf("%d", solve(0));
}










Fast editorial!!
Love you!!! Thank you posting Editorial this quick.
Still, no news of last round's editorial
Excellent problems! Lightening fast editorial! What more does one need!?
Can someone please explain D? I cannot understand the editorial.
You can also ternary search the x-coordinate of the circle's center and judge the better side by calculating the minimum necessary radius. Let's assume the x-coordinate of the center be x0, then the center should be (x0,R). We enumerate all points (xi,yi) and find out the minimum radius separately for each point, which will be the R in equation like: (x0-xi)^2 + (R-yi)^2 = R^2. The maximum necessary R will be the minimum radius we need.
hOW TO DO ternary search<>.Thanks in advance
This is a nice explanation of ternary search. Hope it helps.
I know ternary search but how to use here
my analysis ternary search using by X coordinate which from common point with river.
Given: River line (i.e. y=0) must be a tanget to the circle.Hence your centre point will be some (X,Y) where Y is the radius.
Now find minimum Y(Use binary Search) and slide circle left to right ,to and fro (ternary search), there will be some x such that it contains all the points that satisfy for y ( if valid).
Fix your x with ternary search , then find min R , for which circle (x,R) contains all points, and decide ternary search domain on basis of min value of R.
2nd approach is efficient one.
For D, I did a ternary search to find the X coordinate of the center of the circle. Then calculating the radius is easy.
Bro can you explain in little more detail
D can also be solved with a randomized algorithm much like the one used in minimum covering circle problem. The only thing to change is to make the new circle always tangent to x-axis.
What is wrong in this solution? Is it the precision errors for doubles in Java?
Yup I guess so. Same thing happened to me in c++ as well. You can improve it by writing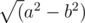 as
as 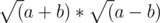
Thanks!! I also tried this r2 - (y - r)2 = y2 - 2yr, where y < 107, r < 5 * 1013. So we get rid of r2 which is big. Passed Test #4, but failed on #6.
you need to do sqrt(y^2 — 2yr) = sqrt(y)*sqrt(y — 2r) because y*r is also too big.
You can also just change your binary search bound from 0...1e15 (I'm guessing you have) to 0...1e16 and it'll magically pass with your first original equation.
In the Code for problem 1059C - Sequence Transformation, it is sufficient to generate the required answer from
nandmulonly without using the global arrayint seq[maxn]. In particular, when n ≥ 4, the number of timesmulis appended to the answer array should be exactly equal to the ceiling of n / 2, regardless of the contents ofseq. The following is an Updated Code.Could you please elaborate more?
It is well-known in integer numbers arithmetic that an integer sequence $$$1,2,\ldots,n$$$ has exactly $$$\lfloor \frac{n}{2} \rfloor$$$ even numbers and $$$\lceil \frac{n}{2} \rceil$$$ odd numbers. Note that the requested numbers can be written to the standard output stream on the fly without having to store it in the global array
ans[].90393879
In another comment on this problem, I wrote the following note: starting with problem size $$$n \ge 1$$$ and GCD $$$g = 1$$$,
the present sequence can be expressed as $$$[g, 2g, 3g, \ldots, n g ]$$$,
the answer to the three base cases when $$$n \le 3$$$ are $$$[g]$$$, $$$[g, 2g]$$$ and $$$[g, g, 3g]$$$, respectively, and
the reduced recursive case when $$$n \ge 4$$$ is the same problem with problem size $$$\lfloor\frac{n}{2}\rfloor$$$ and the GCD is $$$2g$$$, where $$$g$$$ is appended $$$p = \lceil\frac{n}{2}\rceil$$$ times to the answer before solving the reduced problem, removing from the present sequence all $$$p$$$ odd multiples of $$$g$$$ that are not divisible by $$$2g$$$, typically $$$[g,3g,5g,\ldots,(2p-1) g]$$$.
Can anyone give more detailed explanation of B please?
My solution is to check if there are exactly 8 inked cells around a cell(not empty).If so, just put a pen on a new sign.After that, compare the new sign with the given one and you can know it's YES or NO.
my solution is as follow --> i have checked if cell(x,y) is '#' or not. if it is, than i have checked for all 8 adjacent direction to it that whether at least one out of 8 it is possible to make 3X3 matrix.if it is than we can fill this cell and ans is YES and it is not possible to make 3X3 matrix than NO.
--> if cell is not '#' than continue.
my solution is . http://codeforces.net/contest/1059/submission/43840425
please anyone explain,in problem c, why this algo. works?
The gcd(a, a+1) is always 1. So in order to maximize lexicographically the sequence, you have to remove all the consecutive pairs. The best option to do that is to remove the odd numbers in which the gcd will be always 1. So if you have 1,2,3,4,5,...N and you remove the odd numbers you have now 2,4,6,8,... = 2(1,2,3,...floor(n/2)).
Well explained but we need to consider when n=3. Here is the implementation of same.
http://codeforces.net/contest/1059/submission/43883859
How can you prove that for the problem 1059C, the rest of the answer is the answer for floor(n/2) multiplied by 2?
Nevermind, i just figured it out. Thanks
How? Can you please tell?
And How it is an nlog n solution? It seems to be O(n) solution
The gcd(a, a+1) is always 1. So in order to maximize lexicographically the sequence, you have to remove all the consecutive pairs. The best option to do that is to remove the odd numbers. So if you have 1,2,3,4,5,...N and you remove the odd numbers you have now 2,4,6,8,10,... but that is equal to 2*(1,2,3,...floor(n/2)). From there is direct that the rest of the solution is the solution for floor(n/2) times 2
Thanks a lot
the running time of the code for problem C is O(n) and not O(nlogn)
Yes, I think time complexity is O(n). We build the output of size n.
Fixed, thank you.
For problem E can someone please explain the solution a lttle bit easy way. I can't understand the intuition behind the solution that why it's optimal?
Consider if you are at a node in a dfs, and all the children are all already part of a chain. Obviously you can only continue one chain from one of your children, and possibly you have to start a new chain if the children's chains are too long.
So for each of the children, just take the one that will allow you to add the most amount of nodes in the future. The reason is that for any of the children's chains, all their ancestors that could be added later are the same, so you might as well take the chain that can be extended the furthest possibly later. You can check how many ancestors you can add to a chain using binary lifting/sparse table.
"You can check how many ancestors you can add to a chain using binary lifting/sparse table." -> Or simple binary search.
Thanks for the reply!
Что может значить WA 18 в задаче B?
Can anyone tell the use of the statement "for(int i = 0; i < n/2; i++)seq[i] = seq[2*i + 1]/2;" in the author's code?
There was no need. Just comment it out, it will work perfectly fine. seq array was just to keep the positions so that every time odd positions (from the remaining can be removed) but since it is already initialized with i+1, every time it will get alternate even odd. Just dry run for say n=10 and you will understand why it was there and why it works fine without it.
Thanks a lot
D solution:
each point(xi,yi) requires minimum Ri where reserve is (X,0)
Ri = sqrt((yi-Ri)^2+(xi-X)^2)
is interpreted Ri^2 = (yi-Ri)^2+(xi-X)^2
after transposition yi*Ri*2 = yi^2+(xi-X)^2
thus we can find equation Ri = (yi^2 + (xi-X)^2)/(2* yi)
so , R = max( Ri = (yi^2 + (xi-X)^2)/(2*yi) )
Hi, I get your point that Ri = (yi^2 + (xi-X)^2)/(2* yi). As this function is quadratic, we can find it's minima using ternary search. But actual function to minimize is R = max( Ri = (yi^2 + (xi-X)^2)/(2*yi) ). So I this case, I don't get how can we assume R is decreasing then increasing and use ternary search to find the answer. Please help, Thanks in advance!!
draw graph ( X , Ri ), it can interpreted for ( X , (xi-X)^2/(2* yi)+ yi/ 2 ) if you calculated by "partial differential equation" for X , yi is constant number
so , we can guess it is quadratic function
we can imagine many quadratic functions in the field ,than where "max is minimum point" has special feature that there is crossed point (at max Ri)
even near at "minimum point" increasing is larger than two crossed functions which parallel mid go to minimum point.
also you can make skyline that looks similar quadratic function.
so you can try ternary search for X .
Hello everybody. Is it possible to prove problem C? (why it works that way)
As long as you have both both even and odd numbers the gcd is 1, so you need to get rid of either odd or even. It is faster to get rid of odd and get 2 as gcd (for any other number you have to get rid from all evens numbers before, which is profitable only for trivial case n=3). What happens after you delete all odd numbers? All numbers (and their gcd) are miltipliers of 2. So you can divide everything by 2 and get back 1,2,3... — same problem.
hope it helps
In other words, starting with problem size n ≥ 1 and the GCD g = 1,
the present sequence can be expressed as {g, 2g, 3g, ..., ng},
the answer to the three base cases when n ≤ 3 are {g}, {g, 2g} and {g, g, 3g}, respectively, and
the reduced recursive case when n ≥ 4 is the same problem with problem size floor(n / 2) and the GCD is 2g, where g is appended p = ceil(n / 2) times to the answer before solving the reduced problem, removing from the present sequence all p odd multiples of g that are not divisible by 2g, typically {g, 3g, 5g, ..., (2p - 1)g}.
Thanks
Intuition is this.
Imagine if you could remove every number so gcd becomes gcd*k. Well, you have to remove all the other non divisible by k.
Now lets compare what the result would look like if you did it:
1111...22222...444444 111..333..99999
But we can make the observation that it there are less numbers to remove to get gcd -> 2*gcd than other values of k. Because this takes n/2 numbers as opposed to 2n/3, 3n/4 ... which will thus be lexicographically lower.
So it is always optimal to try to remove odd numbers when to rescursively solve.
Edge case is 3, where the amount of odd numbers = non multiples of 3, so we take 3 instead of 2. You can look in my code if interested.
Hello,
Can you please explain what is the advantage of doing middle = sqrt(left * right) in case answer is greater then 1.0 in binary search? [It is code for D problem I am referring to]
Thank you!
Read this post.
For problem D,why do we init R to 1e16? Also, why is l set to 1e-16 and r to 1e16 in the can function ? I think for yi > 0, there is always a possible solution if we can set radius to infinity, am I wrong?
the edge case is (x,y)=(1e7, 1),(1e7, 1e7),(-1e7, 1), (-1e7, 1e7), as far as I remember solutions is smth like 1e15/2
I still don't understand B QAQ Is there anyone can help me.
Just put the pen into whatever possible spot you can, then check if any cell is not painted in the board we make.
My solution to problem C: Determine that we have write first I numbers, consider the last number, let's call it GCD. we know that next number is one of the multiple of GCD. now we know that every multiple of GCD that smaller or equal to n is in sequence now, and every multiple of any multiple of GCD is one of the multiple of GCD. and we know that for a fix number K, there is exactly
floor(n/ K)multiple of K in range of 1 to n. so for every multiple of GCD (let's call it M) we calculate number of multiple of M and between those M that the number of its multiple are maximum we choose the greatest M and forfloor(n / GCD) - floor(n / M)print GCD.Does anyone know whats the problem with test 7 in problem E? Here is my submission. Thanks in advance! NVM solved it
In problem 1059B - Forgery, another O(mn) algorithm is to check all pen locations in the sub-grid 2 ≤ i ≤ n - 1 and 2 ≤ j ≤ m - 1. If none of the eight neighbors at a pen location (i, j) in this sub-grid is empty, then all these non-empty eight neighbors are painted. Finally, all cells in the grid are checked. If a non-empty cell is not painted, then the answer is "NO". Otherwise, the answer is "YES".
43922930
In the Solution for problem D,how do you find the upper bound for the answer .having 1e18 gave me overflow issues,but upper bound of 1e17 gave me ac. https://codeforces.net/contest/1059/submission/43925303(my code with 1e18) https://codeforces.net/contest/1059/submission/43925436(my code with 1e17)
can someone explain how to exactly find the upper bound for the value of the radius?
It's okay if you put it on 1e15.For test
2
-10^7 1 10^7 1
the answer is somthing like 1e15/2.
thanks
you can use __float128 for precision.
problem that you square long double almost 1e18 and subtraction and sqrt makes a little error.
so change some part ld to float128 or how about without sqrt
thanks.didnt know about __float128.will try using it
It is worth noting that in 1059E - Split the Tree you can calculate how far up vertical path that starts in current vertex can go without knowledge of binary lifting.
For every vertex calculate
sum[vertex]— sum of values in all vertices on path from root to current vertex. Traverse tree recursively and maintain stack of parents for current vertex. We can use binary search over this stack to find lastpositionwheresum[current_vertex] - sum[stack[position]]exceeds sum limit in single vertical path. Difference ofpositionand stack size will be the length of maximal vertical path that starts from our current vertex.I've tried to come up to a linear solution for this problem but that was not successful. Can anyone provide a linear solution or prove that it is not possible?
Hi, I believe I have a solution in O(n log* (n)). I just need a DSU. I sort the vertices by height (I can do it in O(n), by count sort), and greedily travel up compressing the paths. Correct me if I am wrong (please).
Some dirty code for this: https://codeforces.net/contest/1059/submission/44409581 but I used STL sort here, so it is actually O(n log (n)), but easy to modify to get O(n log* (n)).
Don't know if we can get linear though.
EDIT: it's not O(n log* (n)) actually, but the time to perform O(n) operations in the DSU structure, so some inverse Ackermann function, or something.
So, If I understand everything correctly, your idea is to pick naive solution (while there is at least one vertex that is not yet included into any path do following: start from the deepest such vertex and start a new path from this vertex, then expand this path upwards as long as we can) and make this observation:
It only makes sense to check upward expansion of some path to some vertex that is not yet covered with any other path. So, instead of naively checking every vertex on our path upwards, we want to quickly skip all vertexes included into other paths and check closest not covered vertex to be included into our path.
This check (can vertex A be included into the path that has its lowest vertex in B) can be done in O(1) with precalculated vertex depths and sums from each vertex to tree root. DSU can help us to keep groups of visited vertexes together and for every group store the highest vertex of that group to quickly find the next unvisited vertex on our path.
Let's prove compexity. In this algorithm, we will cover all the vertexes with the paths and (in worst case) unite all sets of DSU. In details we will repeat this:
Start path from deepest not covered vertex and start path upwards expansion — vertexes can be ordered by depth in O(N) using counting sort
find the closest unused vertex, uniting all groups of covered vertexes together in DSU that we are skipping — O(N·α(N)) in total of all steps
check if we can include found vertex into this path — O(1) for each step
if we can include this vertex into our path then include it and continue expansion, otherwise finish expansion
Steps 1 and 4 will give us exactly N vertex inclusions into groups of used each done in O(α(N)) in total.
So we have O(N·α(N)) solution, where α(N) is inverse Ackermann function (and can be ignored in practical solutions analysis due to its extremely slow growth).
Thanks for sharing your ideas, that is really cool improvement of a very simple solution.
Hi again, the coincidence seems odd, but I have been reading wikipedia recently came accross a note that find-union can be performed in linear time in certain cases (theoretical result). I believe this task meets the requirements, I am not yet sure though (and can't read the whole paper at the moment). You can have a look if you are still curious — https://www.sciencedirect.com/science/article/pii/0022000085900145.
The note on wikipedia was on https://en.wikipedia.org/wiki/Tarjan%27s_off-line_lowest_common_ancestors_algorithm, and I got there from https://en.wikipedia.org/wiki/Cartesian_tree, but that is not that important.
EDIT: So I believe we actually CAN solve this task in O(n) !! What a win.
hi, with help of your ideas and solutions i used path extension and the problem can be solved in O(n) i think. Here is a link to my solution- https://codeforces.net/contest/1059/submission/56407865 though here i have used algorithm::sort , but if we use counting sort then i think time complexity would be reduced to O(n) as all vertices will be visited atmost 2 times and we wont need DSU.
https://codeforces.net/contest/1059/submission/43989515
what's wrong with this solution of problem C can anyone please point out ...
your code didn't consider 3 exponent but consider only at case of 2
didn't get D problem's editorial
I have solved E with greedy and a strange binary search.
If L is + ∞,we can use greedy:we must consider leaves first,so every node(except leaves) will join the son with minimum value if the son's value and the node's value are not exceed S,else the node's value is its number.
To ignore L,we can binary search C that every node's number will add C,then do the above greedy,if the vertical path with maximum number of nodes is not exceed L,then decrease C,else increase C.
This is my submission.However,I don't know whether I'm right.If anyone knows how to prove it or prove it is false,please reply to me,thanks:)
ps:My English is poor,if you are Chinese,you can talk with me in Chinese.My email:[email protected]
In problem E, the second solution's code, some of the '-' maybe make mistake and it becomes '—'. Please modify it correctly. Thank you.
Fixed, thank you.
.
Can someone give me ideas/methods to reduce my floating-point precision for the ternary + binary search solution?
Tried binary search — style ternary search for like 20 times, couldnt get it to work.
Still can't get it precise enough for the ternary search, and im out of ideas to optimize (already spent like 6 hours on trying random stuff lol).
https://pastebin.com/sCFbMcyV
Any ideas/suggestion will be highly appreciated
I am having a hard time with precision in problem D any suggestion will be appreciated 44064198
Try changing (high >= low) to something like (low-high < EPS) and set the epsilon to 1e-8 or something.
How is something like this passing E 44173661?
Pretty sure this hits N^2 behaviour if you make a tree where you have a chain and then at the end of it it spreads out...
Consider the following for problem E:
Setting n = 1e5 will time out many naive greedy solutions (approx 5000ms on csa editor, cf custom invocation limits input size) such as mine
Can you please add such a case because as of right now a whole bunch of N^2 solutions are "shortest solution size" or whatever but actually shouldn't be passing the problem
1059E - Split the Tree: there is a simple small-to-large, $$$O(n\log{n})$$$ solution. You can read about small-to-large here.
Perform a dfs on the tree; for each node $$$s$$$, store in a set the possible nodes $$$v_1$$$ such that $$$s$$$ and $$$v_1$$$ are in the same vertical path. You can efficiently calculate the answer for each $$$s$$$ by iterating over its children and by merging the smaller set to the larger one. In the meanwhile, for each node you have to delete "impossible" paths (with sum of weights $$$> S$$$ or length $$$> L$$$): these conditions can be checked by calculating prefix sums over the vertical paths. Then, if the set of $$$s$$$ is empty, you have to start a new path from $$$s$$$ by inserting it into its set, and increase the answer by $$$1$$$. This is $$$O(n\log^2{n})$$$ (because of sets), but it's enough to pass all the tests. 95353675
To improve the complexity, you can use simple vectors instead of sets, and put an additional flag on each element of the vector ($$$1$$$ if $$$v_1$$$ is still valid, $$$0$$$ if it's invalid). Then, the condition "the set is empty" becomes "all flags are set to $$$0$$$".
UPD: I've just realized that this is $$$O(n^2)$$$ if the tree is a line with large $$$L$$$ and $$$S$$$. Even if sets are merged with small-to-large, each path can be checked up to $$$O(n)$$$ times.
Please explain me the error in Problem D, I have tried for a day now. My approach is doing binary search on radius.
I did binary search on radius, and to check whether such circle is possible, I take first the circle at $$$(0, r)$$$ where $$$r$$$ is mid of binary search. Now I calculate necessary shifting to align leftmost offset point into the circle left boundary. Then I check all points whether they lie inside this circle.
I am having some precision issue I think. In pretest 4 it is giving error of 0.000005, and I think it is settling for radius smaller than the optimal radius.
Please help me.
submission