This is a common subtask in many geometry problems. Today I was unable to solve 1059D because my point-to-point distance calculation is not accurate enough. To summarize the problem, "Find the smallest circle which encompasses all the points, such that its border touches the x axis." I understand there are other ways to solve the problem, but I really want to learn to complete this subtask accurately, since it's recurring in many different problems.
Here's how I would usually calculate it:
double xDist = Math.abs(x1 - x2)
double yDist = Math.abs(y1 - y2)
double dist = Math.sqrt(xDist*xDist + yDist*yDist)
However, this was failing test #4 due to double precision issues. I got some help with this and refactored the calculation into:
double dist = Math.sqrt(xDist) * Math.sqrt(yDist) * Math.sqrt(xDist/yDist + yDist/xDist);
Somehow, this was still not enough. I don't understand how I could possibly calculate distance between 2 points more accurately with Java doubles. Can you help me out? I condensed the failing test case into very little code here.











If you just want to compare distances, you can compare squared distances. That way you have no precision error. Often you can solve problems while only taking one sqrt of the squared distance at the end. I'm not sure if this is applicable here though.
I tried this, but still run into the same problem.
No, you didn't try that. You're comparing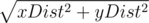 and r, and what you should do is compare the squares of there numbers: xDist2 + yDist2 and r2.
and r, and what you should do is compare the squares of there numbers: xDist2 + yDist2 and r2.
Yes I did try it, and no, it doesn't work. I created another minimalist example from test case 4 to prove this: https://pastebin.com/mMvLQwpi
use long long instead of doubles
But the distances can be fractions. For example, test #1 fails when everything is long instead of double. Or maybe you mean only some of the calculations should be in long long, some should be in doubles?
oh i am wrong, yes distances can be fractions
Why the downvotes?
using doubles and calculating the dist like you did is perfectly fine for this problem... the precision loss probalby happens somewhere else... (a solution which uses doubles: https://codeforces.net/contest/1059/submission/44052169)
Did you look at the condensed example case https://pastebin.com/bgDKxiJe ? It shows that the precision loss does indeed occur at the distance calculation. I'm not entirely sure what's going on in the solution you linked, but many solutions to this problem use doubles to do different calculations than point-to-point distances. It looks to me like that solution is also doing something else, not calculating point-to-point distances.
I tried a ton of tweaks, and I was able to reduce the error by half!
https://codeforces.net/contest/1059/submission/44053130
Unfortunately it's still not enough to pass.
The only advice I have for you is switch to C++.
Ouch! In any case thank you for the effort :(
you can even more increase the precision of floating point calculations in java by NOT storing them in variables... (this is weird but ok...) https://codeforces.net/contest/1059/submission/44053604
So close. Maybe one day far in the future scientists will be able to solve this problem.
44074086 I think I made it quite precise, but the output is 2 times less than it should be...
if (yDist > 1e9) dist = yDist+xDist*xDist/yDist/2;Please explain?
Since yDist * yDist doesn't fit in long, I used an approximation if yDist is very large. Though I realized that part is actually where the error is; it should be something like xDist * xDist / 2.0 / yDist, but that gives the answer of about 4.973E13, which is too inaccurate.
I tried looking at your could but couldn't manage to find the problem. However, I believe that even if you managed to find the precision problem you'd still receive a TLE verdict with this solution, since you do a binary search on the radius and, for every radius, a ternary search on the X coordinate of the center of the circle. It's possible to exclude that ternary search by finding, for every point, an interval of X coordinates of where the center of the circle could be and simply check if the intersection of such intervals is empty or not.
If you're having precision issues when measuring distances, first of all you should buy a ruler with a smaller scale. If you're still having trouble, wear glasses and take some medications to prevent your hand from shaking when holding the ruler.
I was able to get it to test 6 but I have no idea on how to make it more precise (I eliminated the need for ternary search inside the binary search and some other changes). https://codeforces.net/contest/1059/submission/44082804
Also, why do you have 1400 lines of template?
The 1400 lines of template is my contest library. I like to keep it in the same file so that I can instantly use anything I need.
I found it!
p.y is an int and p.y*p.y overflows
Edit: https://codeforces.net/contest/1059/submission/44097466
Oh well... That's what happens when you debug something that is hidden under 1400 lines of template that's not yours :P Edit: https://codeforces.net/contest/1059/submission/44097400 it passed
Sorry about that :( For what it's worth, I did post a minimalist example of the problematic code that didn't have 1400 lines of template (though it was too minimalist to be a CF submission, so I understand why you would rather start working from my CF submission rather than the minimalist example).
I'm not completely sure how this passing solution works, but I guess it's not calculating point to point distances?
It's not. It calculates the range [l, r] in x that the radius can be. If that range is not empty, that radius is ok.
Thanks!
Hey, as someone who had similar issues to you, my advice is to not do a<=b to compare very large floating point values.
Why? Because the mantissa will easily cut it off.
Instead of something like a < b, try something like a-b < epsilon where the epsilon is 1e-8 or something. Good luck!