Tenka1 Programmer Contest / Tenka1 Programmer Beginner Contest will be held today (time).
The writer is DEGwer.
Tenka1 Programmer Beginner Contest
The point values will be
Beginner contest: 100 — 200 — 400 — 500
Programmer Contest: 400 — 500 — 700 — 900
Let's discuss problems after the contest on community Discord server










My idea for F (idk if it's correct, I couldn't finish in time): - if the number of times the operation is performed is K,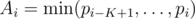 - that means K is the number of occurrences of 1 - the occurrences of 1 need to be consecutive; for each other number, it must have exactly one pair of consecutive occurrences at distance ≥ N / 2, which give us a range with size < N / 2 - everything in this range for i must be ≤ i; if it has length l, then there's a range of up to K - l + 1 possible positions for the original pj = i - if each pj is within its range of allowed positions, each number in the resulting sequence is ≤ Aj - each Aj = i gives a set of pj ≥ i; if this is all satisfied, each number in the resulting sequence is ≥ Aj - removing the set of forbidden positions (a union of ranges with length K) from each range of required positions still gives a range - we need to count permutations where pj = i means
- that means K is the number of occurrences of 1 - the occurrences of 1 need to be consecutive; for each other number, it must have exactly one pair of consecutive occurrences at distance ≥ N / 2, which give us a range with size < N / 2 - everything in this range for i must be ≤ i; if it has length l, then there's a range of up to K - l + 1 possible positions for the original pj = i - if each pj is within its range of allowed positions, each number in the resulting sequence is ≤ Aj - each Aj = i gives a set of pj ≥ i; if this is all satisfied, each number in the resulting sequence is ≥ Aj - removing the set of forbidden positions (a union of ranges with length K) from each range of required positions still gives a range - we need to count permutations where pj = i means 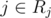 , where ranges Rj can be computed as described above - I think no two of these ranges may overlap — this should be ensured by removing the "forbidden positions", so the solution is just the product of ranges' sizes
, where ranges Rj can be computed as described above - I think no two of these ranges may overlap — this should be ensured by removing the "forbidden positions", so the solution is just the product of ranges' sizes
UPD: It works. The maxtests are kind of weak — only 4 gave TLE for a semi-bruteforce solution.
If you use sync_with_stdio + cin + g++ compiler, don't do it!
https://beta.atcoder.jp/contests/tenka1-2018/submissions?f.User=dalex
Problem E has just 100 KB of input. Just N, M <= 300 and N strings of length M.
In my last four submissions, the only differences are:
Also it's interesting that for this particular problem my solution worked faster on clang, but that's not always true.
Nope. Maybe the problem is
char*instead ofstring.I had a somewhat different way to think about E using the L1 norm. Start by transforming the points from (x, y) to (x + y, x - y). Then the distance between two points is the maximum (rather than the sum) of their absolute differences in the two dimensions.
Fix the side length of the equilateral to be D. Each pair of points should differ by exactly D in one dimension and by at most D in the other. It is impossible for all three pairs of points to differ by exactly D in the same dimension. So both dimensions have some pair of points differing by exactly D.
Order the points by x-coordinate. We know x1 ≤ x2 ≤ x3 and that x3 = x1 + D. If x1 < x2 < x3 then the middle point should differ from both of the others by D in its y-coordinate, and we see that y1 = y3 = y2 ± D. If we fix (x1, y1), we can count the number of such triples in O(1) using prefix sums. We can also rotate the grid and perform the exact same procedure to count triples such that y1 < y2 < y3.
Now suppose that neither dimension has three distinct values. Then either x1 = x2 or x2 = x3, and either y1 = y2 or y2 = y3. It is still true that x3 = x1 + D and y3 = y1 + D. Once again by fixing (x1, y1) we can count the total number of such triples in O(1).
Overall the runtime is O((N + M) * N * M): number of different values for D times number of points we can fix as (x1, y1).
Nice