Hello!
During yesterdays round I solved (or tried solving) problem D with suffix automaton — it's very simple after copying SA's code (link to code). But unfortunately it TLE like the majority of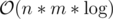 
solutions. So I just thought "Eh, I guess 
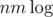solutions aren't supposed to pass". But today I actually realized that I'm not sure if my solution is actually 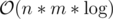— in the part where we create the "clone" node, we copy the adjacent nodes of the given node to the adjacency list of the clone. This might actually result in O(Σ) complexity and if this happens many times the solution will obviously be slow. But I cannot find a sample, where we happen to copy large adjacency lists many times. Can you help me with that?
So generally my question is:
If we use suffix automaton on large alphabet what is the worst time complexity?
PS: We can achieve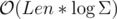 
if we use persistent trees to keep the adjacency lists, but I find this to be a very ugly approach.
Depends on how you keep it in memory. But it won't have more than 3*n edges overall.
If done like this, the complexity of SA construction does not depend heavily on the size of the alphabet. Your solution TLEs simply because there are too many map insertions/copies for the given time limit.