awoo's blog

Educational Codeforces Round 54 Editorial
By awoo, history, 6 years ago, translation, In English

1076A - Minimizing the String

Tutorial
Solution (Vovuh)

1076B - Divisor Subtraction

Tutorial
Solution (PikMike)

1076C - Meme Problem

Tutorial
Solution (adedalic)

1076D - Edge Deletion

Tutorial
Solution (BledDest)

1076E - Vasya and a Tree

Tutorial
Solution (Ajosteen)

1076F - Summer Practice Report

Tutorial
Solution (PikMike)

1076G - Array Game

Tutorial
Solution (BledDest)
  • Vote: I like it
  • +49
  • Vote: I do not like it

Comments Comments (32)
| Write comment?
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

My solution to problem E:

first for each depth sort all vertices by starting time and for each query and vertex U with starting time between starting time V and finishing time V, we add x to ans U (by partial sum, ask in reply for more information). then for all vertex U with starting time between starting time V and finishing time V, in depth height[v] + d + 1, we subtract ans[U] by x (by partial sum). and after all queries we run a dfs and find ans for each vertex.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Fun to see someone that used the same idea (:

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it -10 Vote: I do not like it

    I know it's quite old comment but still (by partial sum, ask in reply for more information) please explain the partial sum approach. Thanks

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +7 Vote: I do not like it

The problem E can be solved with complexity O(N + M) without sorting or any trees by the next way. We can remember all queries for each vertex V as pairs (X, D), which mean we have to add X to all such vertexes U in the subtree of V that the distance between U and V isn't greater than D. Then we can do DFS.

Let ANS be the current answer. Also we have to get an array CHANGE meaning that when we visit a vertex V we have to decrease ANS by CHANGE[depth[V]], where (obviously) depth[V] means depth of V. So when we visit a vertex V, for each pair (mentioned above) in V we have to increase ANS by X. Also we have to add X to CHANGE[depth[v] + D + 1].

And we must decrease ANS by CHANGE[depth[V]] once. So answer[V] = ANS. When we leave V, we must undo all changes we did in this vertex.

That's all. (I hope, I was clear).

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks, your strategy worked perfectly for me.

    I realized this problem is basically a generalization of a problem for arrays where one begins with $$$a[\cdot]$$$ all zeros, and receives updates of the form $$$(l,r,x)$$$ meaning $$$a[k]+=x$$$ for every $$$l \leq k \leq r$$$, and after all updates, one needs to recover the array $$$a[]$$$. One could use segment trees for a $$$n \log n$$$ solution, but as in this case it is overkill because queries occur after all updates. (for future readers, the linear time solution for the array problem is to keep an extra array $$$change[\cdot]$$$ with the operation $$$change[l] += x$$$ and $$$change[r+1] -= x$$$ for every update)

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I cant understand this implementation for D.

if(d[to] > d[k] + w)
			{
				q.erase(make_pair(d[to], to));
				d[to] = d[k] + w;
				last[to] = idx;
				q.insert(make_pair(d[to], to));
			}

How does he erases something from the set q berfore adding it?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why does the following implementation for problem D is giving TLE in TC 67 (I have followed the idea given in editorial) . Here is my implementation [CODE]

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    It's because you used Java.

    On the serious side though, it's because in dijkstra, you need to ignore the node if you've already visited it. Add a line like if (vis[p.st]) continue;.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

sorry for my english but in problem D, according to your algorithm, asume that we need to find the shortest path from vetex 1 to all the others, so we just need n — 1 edges and from that n — 1 edges, we can get all the shortest path from 1, right ? (It just like MST, in MST we need n — 1 edges to get MST, but now, we also need n — 1 edge to get all the shortest path from 1 to another vetex)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yes. The tree we are building this way is called shortest path tree. In fact, Prim's algorithm of building MST and Dijkstra's algorithm of finding shortest paths are really similar, so we can use the tree built by Dijkstra's algorithm to store all shortest paths.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone help me to figure out what's wrong with my code problem 1076D — Edge Deletion https://codeforces.net/contest/1076/submission/45743114

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Suppose there are two edges like (1, 21) and (12, 1). toString(u) + toString(v) will return a string "121" in both cases, so there is a collision. Maybe adding a delimeter or using a pair of ints instead of a string will help.

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

About G: It turns out that it can be reduced to O(m(n+q)logn) if we will use the distance to closest losing state instead of a mask of winning and losing states.

I don't know how to maintain the status by this method. Can anyone explain this?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    Well, in my solution I consider all possible masks of next m states of dynamic programming. As far as I understood some participants' solutions, they use the fact that only the next winning state matters, so, for example, masks like 01001 and 01000 are exactly the same and can be represented as 01xxx. So we may consider m + 1 different situations: m for every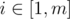 considering the distance to the next winning state, and an extra situation when the next winning state is too far away to be reached.

    Maybe Anadi can explain this idea better.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In my solution I want to know for every position i — can I win if I start in this position. Let's say that if I can win then this position is good. I say that if ai  ≡  0 mod 2 then position i is good. Why? Because if there is a position j such that it is not good then I can move to it, otherwise I can stay in the same position and my opponent has to choose a winning position for me.

      Using this fact we can easily solve this task in O(nq) — we pick last position for which we don't know answer, if it's even then it's good, otherwise it's bad and we can mark previous m positions as good.

      We can simulate this process faster if we divide out array into blocks of size so final complexity is 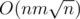. It was possible to solve it faster in 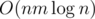with segment tree (it's practically the same as model solution).

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thanks for the help:) I think I've understood

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What does the last array in the code for problem D do? Thanks

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This array maintains the index of the last edge on the shortest path from 1 to every other vertex.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

awoo There's a typo in the editorial of problem F. The following 2 lines are the correct ones.

1) ... the smallest number of separators you can have is ...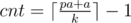

2) ... The smallest number of separators is ...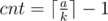

The expressions used in code, however, is correct.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Whoops, sure. Fixed, should be ok in a couple of minutes.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve problem E(Vasya and a Tree) for online queries?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Why this: 1+(n−d)/2 for Problem B?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Let d be the initial smallest prime divisor for n.

    After finding d, we subtract it, so we have done 1 operation total.

    Now, n-d (n after subtracting d) is guaranteed to be even, so for each subsequent operation we will always find 2 and subtract it. We will do (n-d)/2 operations like this.

    So we do 1 + (n-d)/2 operations total.

    Why is n-d always guaranteed to be even? There are two cases:

    1) n is even. So d is even. So n-d is even because even-even=even.

    2) n is odd. So d cannot be 2 and 2 is the only even prime number. So d is odd. So n-d is even because odd-odd=even.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem C, how do we get a, b = (d±√D) / 2?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Problem C I tried using a binary search solution. Link: https://codeforces.net/contest/1076/submission/46646184

I'm doing binary search from 0 to d. I take the mid element as a and find b = d — a. To break out of the binary search I check if a*b == d and return a or if mid becomes equal to either a or b (I figured they might after one point because of precision) in which case I return -1 indicating it is not possible.

This is not working for all test cases and I think it's off by some precision cause it isn't passing the sample. What is the correct way to do this if it were to be done using binary search?

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Help required in problem 1076D-Edge Deletion. http://codeforces.net/contest/1076/submission/59660020

What I am doing is over here is,first find the MST of the given graph. And then run a dfs on this MST and keep adding edges until the count is less than k. What is wrong with this approach??

→ Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    test case (format as of problem first number is vertices in graph , 2nd is edges , k , then edges description) 3 3 2 1 2 2 2 3 1 1 3 2 Draw MST and see the difference for vertex 3 , shortest distance via mst approach will be 3 unit , but if you just considered simple edge of 1-2 and 1-3 , shortest path to vertex 3 will be 2 unit. Hence mst may cause problems , better to use dijkstra from single source.

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I learnt a lot from Problem E. Thanks.

→ Reply