Can anyone please explain me easier way the question (question link given below). I didnt understand the question since my geometry knowledge is very low. Also It would be great if you explain also the solution for the problem actually I didnt solve any problem from geometry.
Sorry for my poor English. Thanks In Advance https://codeforces.net/contest/1096/problem/C











Without losing generality, it can be assumed that a regular polygon G with n ≥ 3 vertices is centered at the origin, and that it is circumscribed by a unit circle with radius R = 1 that passes through all these vertices. Note that G consists of n identical isosceles triangles with angles {90 - 180 / n, 90 - 180 / n, 360 / n} degrees and sides {1, 1, 2 sin(π / n)}. Vertices of G can be enumerated as V = {0, 1, ..., n - 1}, such that vertex is located at polar angle θi = 360 × i / n. Let us assume that the triple T = {a, b, c} is a subset of V such that 0 ≤ a < b < c ≤ n - 1. It can be shown that
is located at polar angle θi = 360 × i / n. Let us assume that the triple T = {a, b, c} is a subset of V such that 0 ≤ a < b < c ≤ n - 1. It can be shown that  , where k = c - a and 2 ≤ k ≤ n - 1. In fact,
, where k = c - a and 2 ≤ k ≤ n - 1. In fact, 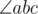 is an incsrcibed angle whose value depends on the polar angle difference between c and a, and is independent of the location of b. The problem is then reduced to the simpler problem of finding the smallest n ≥ 3 for the given integer
is an incsrcibed angle whose value depends on the polar angle difference between c and a, and is independent of the location of b. The problem is then reduced to the simpler problem of finding the smallest n ≥ 3 for the given integer  degrees that satisfies the previous equation.
degrees that satisfies the previous equation.
The following is a C++14 program that generates all the 22 minimum-size regular polygons that include all inscribed angles . The list next to each polygon is the values of the inscribed angle(s) that such polygon includes.
. The list next to each polygon is the values of the inscribed angle(s) that such polygon includes.
https://ideone.com/3Eluk8