1 января 2019 в 23:59 (время московское) стартует первый этап SnarkNews Winter Series 2019. Как и несколько предыдущих серий, SNWS-2019 пройдёт на системе Яндекс.Контест. Опубликовано расписание серии.
По просьбам участников отдельно публикую ссылку на вход в первый раунд. Здесь же по окончании раунда в соответствии с расписанием можно будет обсудить задачи первого раунда.











Как решать B, D?
B: Найти совершенный паросоч Куном, потом превращать его в лексмин по порядку. Берем первую вершину, перебираем ребро из нее в порядке возрастания номера, пытаемся найти цикл через это ребро, который можно прочередовать. Это примерно тот же дфс, что и в Куне. used между дфсами из одной вершины чистить не надо, так что одну вершину обрабатываем за квадрат. Потом надо убрать ее вместе с заматченной из графа.
Это я понимаю. Я не понимаю, что делать если после нахождения парсоча останется нечетное число свопов между последней парой столбцов
UPD. Понял, строк мало и после нахождения парсоча никогда ничего не остается.
Кстати, когда-то давно это обсуждали здесь.
D — была идея, что треугольник ненулевой площади и не содержит внутри или на границе целочисленных точек тогда и только тогда, когда для каждой стороны треугольника противоположная точка лежит на соседней параллельной стороне-прямой. Как такое считать не знаю, но возможно задача была рассчитана на прекалк + OEIS.
Там есть понятный факт, что такие точки являются точными приближениями цепной дроби, за N*M к примеру понятно как решать. Но как решать быстрее все равно не понятно, возможно надо как-то сразу для всех дробей одновременно запускать алгоритм Евклида
Спасибо, почитаю.
F?
Я решал так: за K = 100 шагов с вероятностью очень близкой к 1 все завершится. Для каждой степени простого посчитаем динамику (или формулу) с какой вероятностью оно завершится за не более t ходов. Далее решаем за O(T * K * M). Можно ускорить примерно в M раз, понимая, что мало разных степеней простых в N, но заходит и без этого.
То есть для каждого хода 1... 100 находим вероятность, что соответствующая степень простого перейдет в 1 и перемножаем, отнимая сумму произведений вероятностей, что закончится до?
UPD Достаточно отнимать, что все остальные степени перейдут в 1 за K-1 шагов
Е?
Действуем жадно с концов, подстроки сравниваем хэшами. Доказать жадность довольно легко от противного. В сумме надо сравнить ровно |S|/2 строк
А, действительно. Понял, спасибо.
Перевернем строку и вставим ее в саму себя (s1sns2sn - 1... sn - 1s2sns1). После этого нужно разбить строку на максимальное количество палиндромов четной длины. Решается жадником с манакером (или деревом палиндромов, даа).
Получается, что Манакер нужен только для проверки, что текущая подстрока четной длины является палидромом?
не люблю хэши, да
Идеи по С?
Напишем dpi — минимальное кол-во отрезков, на которые разбиваются первые i чисел. Тогда обновляем dpi через dpi - 1, если число не положительное, и через минимальное состояние j такое, что pri - prj > 0, всегда. Эти состояния будут образовывать некоторый префикс позиций, если отсортить по величине префикс-суммы. Там уже можно пожать все префикс-суммы и делать все в фенвике, например.
Спасибо, я оказывается имел ввиду D (спросили выше) :)
С — можно было еще искать подходящее дп через оффлайн в ДО или честно онлайном в динамическом ДО или treap.
Как решать C из второго раунда?
Заметим, что каждое ребро лежит максимум на одном цикле. Найдем все эти циклы дфсом, остальные ребра гарантированно лежат в остовных деревьях. Также заметим, что из каждого цикла ровно одно ребро не принадлежит остовному дереву. Теперь будем итеративно по циклам строить возможные остовные деревья по циклам и добавлять их в кучу, на каждом шаге выбирая минимальное частичное остовное дерево и добавляя следующий цикл без одного ребра. Сложность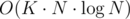 .
.
Выглядит на тоненького очень по тл)
Пришлось поменять multiset на priority_queue, чтобы уложиться в ТЛ :)
Интересно, такое решение заходит меньше, чем за секунду. А на контесте O(KMlogK), в котором после рассмотрения каждого цикла все деревья сортировались и оставлялись K лучших, падало по TL.
У меня на максимальном тесте работает 2 секунды. Вроде можно уменьшить количество элементов в очереди, если хранить не пару (вес дерева, номер цикла), а тройку (вес дерева, номер цикла, позиция в цикле).
За 0.8 отрабатывает следующее:
Забавно, но у меня совершенно идентичный код, который работает в 2.5 раза дольше.
UPD Далеко не идентичный, улучшенная версия работает в 3.5 раза быстрее.
Дело, скорее всего, в том, что я из всех циклов удалил самое тяжелое ребро, поэтому могу сразу помещать в ответ текущий вес.
Точно, фишка в этом, спасибо!
Я не запихал, зато потом сделал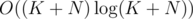 . Отсортируем ребра внутри каждого цикла по убыванию, потом перейдем к разностям соседних. Теперь циклы отсортируем по этим векторам лексикографически (на самом деле важно только что по первому элементу отсортировано). Состояние — какой цикл мы сейчас обрабатываем и на какой позиции находимся. Казалось бы, когда мы переходим к следующему циклу, нужно перебирать, к какому именно. Но из-за отсортированности по первому элементу можно всегда переходить к следующему + надо добавить переход "на текущем цикле не брать ничего и перейти к следующему", все переходы не уменьшают вес, поэтому Дейкстра работает. В итоге на каждое увеличение ответа на 1 мы тратим
. Отсортируем ребра внутри каждого цикла по убыванию, потом перейдем к разностям соседних. Теперь циклы отсортируем по этим векторам лексикографически (на самом деле важно только что по первому элементу отсортировано). Состояние — какой цикл мы сейчас обрабатываем и на какой позиции находимся. Казалось бы, когда мы переходим к следующему циклу, нужно перебирать, к какому именно. Но из-за отсортированности по первому элементу можно всегда переходить к следующему + надо добавить переход "на текущем цикле не брать ничего и перейти к следующему", все переходы не уменьшают вес, поэтому Дейкстра работает. В итоге на каждое увеличение ответа на 1 мы тратим  .
.
Авторское кстати O(KN). Будем добавлять циклы по одному и поддерживать K лучших вариантов в отсортированном порядке. Когда добавляется очередной вариант, нам нужно из объединения двух отсортированных массивов оставить K лучших вариантов, для этого нужно сделать merge за линию. Добавлений вариантов O(N), следовательно общее время работы O(KN).
Разве первое решение не будет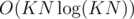 ? Если циклы будут выглядеть следующим образом:
? Если циклы будут выглядеть следующим образом:
1 1 ... 1
1 100000
1 100000
...
1 100000
В конце в очереди должно храниться KN элементов.
Не понимаю, как от теста что-то зависит. Формально за каждое продвижение к ответу (которых K) я делаю O(1) операций с map.
Код для устранения непонимания.
Фишка получается в удалении максимального ребра, тогда будет как раз максимум K вытаскиваний из очереди.
Ну в очереди лежат только остовы. У меня немного другое решение как бы.
Разобрался, крутое решение, спасибо!
Кстати, O(KN) можно получить, используя вместо сортировки nth_element.
Это в каком решении?
Во втором. Просто сливать по одному не обязательно. Можно собрать все в один список и один раз частично упорядочить с помощью алгоритма поиска к-той порядковой статистики.
O(KN) памяти, неоч.
А, вместо merge делать k-th element. Ну это как-то "ЗАЧЕМ". Но да, работает.
Крутое решение, не ожидал, что за такую асимптотику решается
Как решать А с третьего раунда? Я пытался прорелаксировать до линейного программирования, но умею находить только минимальное расстояние, а не максимальное.
Звездочки переберем, теперь надо 27 раз решить задачу без звездочек. Несложно понять, что каждое условие преобразуется в одно или два неравенства вида xi ≤ xj + c. Это стандартная задача, нужно для каждого такого неравенства провести ребро из j в i весом c, а потом посчитать какие-то кратчайшие расстояния (например Флойдом, хотя Фордом-Беллманом в данном случае быстрее; в любом случае нужно быть аккуратным с отрицательными циклами). Доказательство вроде через двойственность в ЛП, кажется я даже видел это как один из примеров в каком-то учебнике.
Спасибо! Отрицательный цикл свидетельствует об отсутствии решения, верно? Можно, пожалуйста, поподробнее о кратчайших расстояниях — нужно среди них выбрать максимальное?
Как решать Е 4 раунда? Я догадываюсь, что можно сформировать массив c1, c2, ..., cn, где ci — кол-во отрезков, покрывающих позицию i, а потом последовательно удалять из него минимумы. Но что-то я не могу из этого получить адекватную формулу для ответа.
На самом деле у нас получается бинарное дерево, при если удалять вершины с конца, то каждый раз удаляется висячая вершина. Таким образом ответ для валидного набора отрезков — это произведение для каждой вершины цешки (общее количество детей в поддереве, количество детей в левом поддереве). Осталось проверить, валидное ли дерево (если нет — ответ ноль). Для этого надо проверить, что l_i <= i <= r_i, есть вершина с l_i = 1 и r_i = n и для любой вершины если отрезки (l_i, i — 1) и (i + 1, r_i) непустые, то они соотвествуют какой-то врешине
О, я даже не понял из условия, что ответ может быть 0. Угу, так понятно, спасибо.
Хаха, у меня была посылка с правильными формулами, но с wa2 только из-за нулевого случая.
Как решать D с четвертого раунда?
Решение основывается на алгоритме Грэхема. Переберём точку, которая будет с минимальной y, x. Меньшие точки выкинем. Отсортируем оставшиеся точки относительно по полярному углу. Теперь посчитаем dp[l][j][k] — минимальная площадь выпуклого многоугольника из l точек, заканчивающаяся на точках j, k.
Большое спасибо!
Как решается C с четвертого раунда? WA39 если это о чем-то говорит
Вначале убирал пары двусторонних вершин, потом жадно шел из верщин нулевой входящей степени, потом разбирал оставшиеся циклы на пары соседних вершин.
Я эту задачу не сдавал, но двусторонние вершины обрабатываются как-то странно. Например тест:
Здесь можно получить две пары, но для этого нужно разорвать пару 2-3
В конце надо еще проверить двойные циклы, что нельзя увеличивающую цепь найти. Я ловил wa39, потому что набажил: вместо == написал !=.
Как решать B, C, D, E, F пятого раунда? У меня совершенно нет идей по этим задачам.
Моё решение B мне немного громоздко. Каждое утверждение задаёт бесконечное множество отрезков t, в которые загорается зеленый цвет, чтобы наблюдение было верно. В диапазоне [0,g+r+y) каждое утверждение задаёт один или два отрезка. Посчитаем длину отрезков, которые попадают в диапазон [0,g+r+y) и покрываются ровно N отрезками. Вероятностью будет отношение длины с учётом вопроса к длине без него.
По задаче C ключевая идея, что есть очень небольшое количество n, для которых правильные n-угольников имеют целочисленные вершины. Поэтому задача решается за O(n^2 log N).
В задаче F пишется очевидное решение с хешами и дп, а потом доказывается, что оно отработает за O(n2 * количестводелителейn). Проще доказывать, если перебирать сначала количество открывающих скобок.
Спасибо большое! Теперь понятно :)
Задача D
Большое спасибо!