mtr361's blog

Difference Between std::lower_bound(set.begin(), set.end(), val) and set.lower_bound(val)?
By mtr361, history, 6 years ago, In English

On CF 256 Problem A, I use lower_bound to binary search on a std::set. However, I've found that using std::lower_bound(set.begin(), set.end(), val) makes the solution blow up, resulting in TLE (>3000ms), while using set.lower_bound(val) works perfectly fine (~300ms).

AC (358ms): 48402685 TLE (3000ms): 48402684

It appears, then, that std::lower_bound(set.begin(), set.end(), val) is not actually binary searching. What is causing this behavior?

Thank you!

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +47 Vote: I do not like it

See the "Complexity" section of std::lower_bound. In particular, std::set iterators are not random access, so you'll degrade into linear-time performance from repeatedly incrementing iterators.

std::set::lower_bound on the other hand is a specialized implementation that does binary search within the BST, so it takes log time.

→ Reply
»
6 years ago, # |
  Vote: I like it +7 Vote: I do not like it
  • lower_bound(s.begin(), s.end(), value) is O(n). For exmaple it computes the distance between s.begin() and s.end() and this is already O(n). Then it is doing standard binsearch. Generally set<T>::iterator it is not a random access iterator. So you can not easily compute let us say it + 2137.
  • s.lower_bound(value) is O(log n) and uses red-black tree structure for computation.
→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -7 Vote: I do not like it

    I think it is not O(n), but actually O(n*logn*logn).

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +8 Vote: I do not like it

      Well, ok. Maybe I wrote it too fast. But it is O(n log n) at most. it++ is O(log n) so naively we have:

      T(n) = T(n/2) + O(nlogn) Which by master theorem, or just by common sense is O(nlogn).

      But when you are doing it++ from the beginning till end, then you are not traversing the same RB-tree edge twice in the same direction. So I believe there is some amortization. Then it would be O(n) as I wrote.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Complexity
      On average, logarithmic in the distance between first and last: Performs approximately log2(N)+1 element comparisons (where N is this distance). On non-random-access iterators, the iterator advances produce themselves an additional linear complexity in N on average.

      http://www.cplusplus.com/reference/algorithm/lower_bound/

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It doesn't account for the cost of actually moving the iterator (e.g I could do an iterator that is incremented by 1 in O(N) and it will become quadratic)

        Still for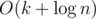 std::set it's easy to see that incrementing by k will work in so overall it will be 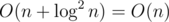. Not sure it's guaranteed by standard though.

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Also in the problem CF1041C, I get TLE by writing lower_bound(s.begin() , s.end() , val).

But in the other hand, there's still some problem that I used lower_bound(s.begin() , s.end() , val), and it does not give TLE. For example, Submission of CF 749D, an another account of me. Can anyone gives me the reason?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -7 Vote: I do not like it

    As fruwajacybyk mentioned, std::lower_bound computes distance between given iterators. If given iterators are random access iterators (as they are for std::vector), then distance is computed in O(1). But for std::set iterators are not random access, but bidirectorial, thus, distance is computed in linear time. Then, while doing binary search, std::lower_bound finds an element in the middle in O(1) for random access iterators, and O(distance) for bidirectorial iterators.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But it's also a problem about set...

      I guess that maybe because of some reasons, the size of one set or the set together is small enough (For example, the sum of their size do not exceeded 1e5), so that the total computed time is fast enough to pass the problem. :)

      P.S. My English is bad, please don't mind.

      → Reply