Topcoder SRM 748 is scheduled to start at 12:00 UTC -5, Jan 26, 2018. Registration is now open for the SRM in the Web Arena or Applet and will close 5 minutes before the match begins
Editorials: https://www.topcoder.com/blog/single-round-match-748-editorials/
- Problem Writer: misof CF:misof
- Tester: Vasyl[alphacom]
This is the sixth and the last SRM of Stage 2 of TCO19 Algorithm.
Stage 2 TCO19 Points Leaderboard | Topcoder Java Applet | Next SRM 749 — Feb 2
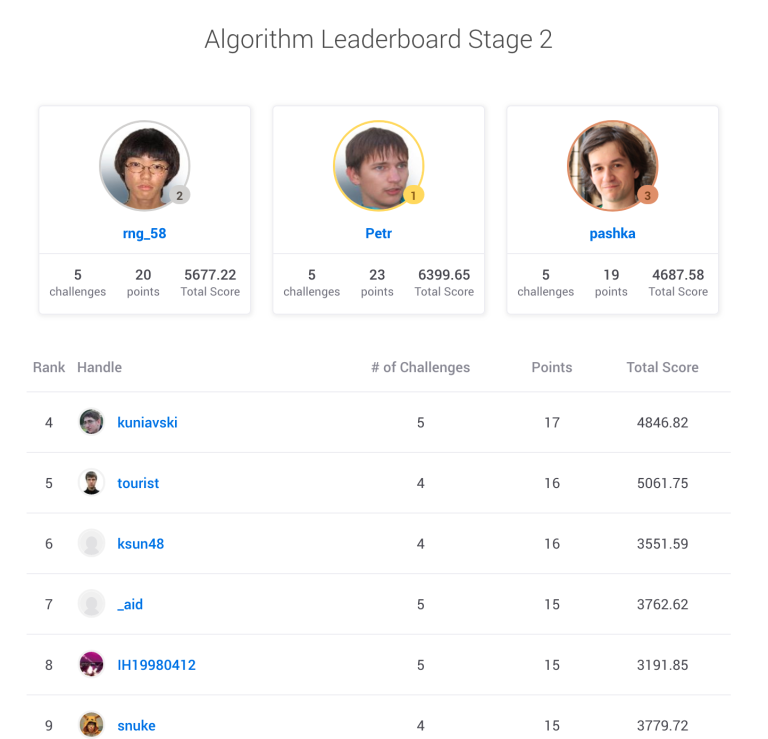
Hope to see most of you competing! All the best!











Clashes occurred.
Match begins in 2 hrs and 30 mins!
the educational round will not end at that time.
Sorry! Yes, We had scheduled it long back and have some product updates afterwards! So won’t be able to move this one.
ok
The arena is timing out for me.
UPD: On again.
div2b took a long time to implement , first time get to know about getline() : )
how to solve div2 C / div1 A ?
DP: Let's f(i , j) be the numbers of subset with gcd == j if we consider only first i elements.
State transitions:
f(i + 1, j) = f(i + 1 , j) + f(i , j) //we don't choose (i + 1)th element
f(i + 1, gcd(a[i + 1], j)) = f(i + 1, gcd(a[i + 1], j)) + f(i , j) //choose the (i + 1)th element
Base case: f(0, 0) = 1
The answer is f(n, goal)
Div. 1 Hard is similar to problem 11 from last years Prime Contest. I don't believe its' possible to come up with idea of nimber multiplication without knowing it in advance. What's the point of giving such a problem?
tourist solve it
Judging by the time it took him to solve it, I'm sure he has seen it before.
See the editorial draft, I explicitly mention a way to get accepted it if you know Sprague-Grundy values but not nim multiplication, just based on guessing a pattern.
In fact, I think this problem is a very nice way to introduce people who know one concept but not the other to this part of combinatorial game theory.
i don't know any of them : lol : )
Didn't understand this part of editorial "it is possible to precompute and store all the 17*17 different SG values we might need". How should it be computed fast?
SG value of a single cell (r,c) can be computed in O(rc) time if you know all SG values (x,y) in the rectangle from (0,0) to (r,c). This is done in the traditional way: try all the rectangles with bottom right at (r,c) and for each of them compute the xor of the SG values of all cells in the rectangle other than (r,c).
(Note that the naive way to do the above is in O(r^2c^2) because you have O(rc) rectangles and you do O(rc) xor-ing for each of them. Still, it's easy to improve it to O(rc) using essentially the same DP that is used for 2D prefix sums.)
Once you realize that in this problem SG(r,c) is some unknown function f of SG1(r) and SG2(c), and that those values are always powers of two, you only need to compute f(2^i,2^j) for all i,j <= 16, and you do this by computing each of the values SG((2^i)-1, (2^j)-1) in the way I described above.
Nice! Does this require 16G of memory (2**16*2**16*4), or is there some way to use less?
You still didn't answer my question =) In addition to Petr's comment I will add that calculation of such huge table of "prefix rectangles" will take not only a lot of memory but also a lot of time.
The DP just needs two rows of the table. The only somewhat-big memory consumption comes for a bit field where you store previously seen SG values.
Here's full code for the precomputation: https://ideone.com/Mh1hFM
It uses around 0.5GB of memory and runs in about 4 minutes on my slowish desktop. (The time can be roughly halved if you know the values on the diagonal, as computing the very last output is cca half of the whole thing.)
Better now? :)
Thanks!
I've almost got it by computing the table for small powers of two and googling the numbers from it. So if googling is an acceptable part of solving a problem for you, this is a great problem :)
Maybe it's just me, but I can't see how a problem about finding a pattern or googling can be great.
I've used to think in the same way, but then I realized that I enjoy such problems as well. Googling can be seen as just another way of coming up with new (for you) knowledge that complements making logical deductions yourself. Both are integral parts of real research work, for example.
I see what you mean. I actually enjoyed some googling problems from Prime Contests and learned cool things from them. These problems can be great when time is not an issue. However in usual contests people who are already familiar with the topic have a huge advantage. That's why I think such problems are bad.
Yes, that's a fair point, too. I guess the subject of googling needs to be obscure enough so that nobody is likely to be familiar with it :)
An example of a problem that's completely broken by googling is 1067E - Random Forest Rank. It's a massive difficulty drop if you find the right thing, and what's left is very standard. I solved it in-contest and had a very good rank, but it didn't, ehm, provide me with any sense of pride and accomplishment.
I don't see why you put those into one bag, "problems about patterns" and "googling problems" are two very different things.
When doing research I quite often needed to discover a pattern, generalize it and prove it. In some competition types you can practice all three steps, but in practical programming contests the best you can get are the first two. (And if one occasionally encounters a problem in which the straightforward generalization is wrong, it can push them towards at least spending some time thinking about whether and why their generalization is correct. Such problems are rare but I've already seen a few.) Discovering nice patterns can be cool, and finding the right generalization is non-trivial creative work.
Regarding googling, there are multiple types of googling problems, and pattern problems are not necessarily googling problems (and vice versa). For example, I see quite a difference between 1) problems where you read the problem statement and it essentially tells you that you need to google obscure properties of planar cubic graphs, 2) problems where you just write a brute force solution and plug its output into OEIS without thinking, 3) problems where you need to do some thinking and some coding to discover what to search for in the first place, and 4) problems from category 3 where your search ends up unsuccessful, either because the problem managed to obscure a known sequence enough or because the sequence wasn't noteworthy enough so far.
Regarding this div1 1000, I still like it a lot because the target group of people 1) has the option to solve it as a problem that is about recognizing and generalizing patterns, and as I mentioned elsewhere in this thread, the fact that after the right generalization one can write a full solution that does not require googling (but does require deep understanding of SG theory) is a big plus in my book; and then 2) has the option to learn about a nice bit of theory by reading the editorial and following up with some CGT resources.
But to each its own. We are not required to like the same types of problems.
In Div1 Easy system tests, is there a case where answer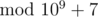 is zero, but the answer itself is nonzero? I've got such a test, but too late to have a successful challenge. The solution passed, but for it to fail, the test has to be a bit more involved than just having such answer.
is zero, but the answer itself is nonzero? I've got such a test, but too late to have a successful challenge. The solution passed, but for it to fail, the test has to be a bit more involved than just having such answer.
My screencast: https://youtu.be/yDrUX0qQIkY
Why was my challenge for this solution — https://community.topcoder.com/stat?c=problem_solution&rm=332045&rd=17397&pm=15289&cr=40842472#defenses not successful? In the solution, yourHomework has the same value as friendsHomework for the first element of the array.
We did indeed manage to have an undetected bug in the checker for the easiest task. Oh the shame.
We'll have the task and challenges rejudged as soon as possible. Thanks for letting us know.