LilyWhite's blog

What is the estimated complexity of this program?
By LilyWhite, history, 6 years ago, In English 
int n;
cin>>n;
if (n==0)//deal with it
for (double i=0;i<=1/(double)n;i+=1e-9)//do something

It seems that, this code runs faster when n becomes larger...

When n = 109, the code will be executed once. When n = 1, it runs 109 times.

So I estimated it as O(n - 1).

But, this means that this algorithm runs even faster than O(1).

How is it possible?

  • Vote: I like it
  • -3
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by LilyWhite (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it -6 Vote: I do not like it

It still takes O(1) operations to read n so O(1 + n - 1).

→ Reply
»
6 years ago, # |
← Rev. 9   Vote: I like it 0 Vote: I do not like it

In Computational Complexity, n often refers to the input size or the problem size. In your code, the input size is constant as only one number is read from the standard input stream. On the other hand, the actual problem size should be measured in terms of the number of iterations that the loop statement performs,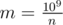 . In other words, m-iteration loops on sequential computing machines in which //do something requires fixed execution-time that does not depend on m should belong to problems with linear time-complexity , even though m is inversely proportional to the input number n. You may check the following performance measurement code: Ideone

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Is it similar to the 0-1 knapsack problem, which can be solved using O(n2) dp but still a NP-Complete Problem?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yes, this is a related issue. The complexity of the exact DP solution of the 0-1 knapsack problem is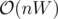 , where n and W are the number of items and the total weight of the items, respectively. Even though the number of items n is linearly proportional to the input size, the total weight W is exponential in the input size, as the maximum item weight is doubled when the word size used to store the item weight value is increased by one bit. You may check Knapsack problem for more information.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        However, as n becomes larger, the actual things this program does decreases. When n exceeds 109, it does nothing.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 18   Vote: I like it 0 Vote: I do not like it

          As mentioned before, considering n as the problem size or as the input size can lead to incorrect conclusions about the linear time-complexity of the m-iteration fixed-time loop. The same can similarly happen in the complexity of the 0-1 knapsack problem. You can simply rewrite W as n × wmax, drop the fixed maximum weight wmax, and Happy New Year! You've got a quadratic time complexity that looks good enough for problems with few hundreds or few thousands of items, even though wmax may be an arbitrarily large value for some of those problems such that the DP algorithm runs for hours on the fastest supercomputer to find the optimal solution.

          If you are not convinced yet, you may just change your loop statement to the following, and check the resulting execution time when n = 109.

          for (double i=0;i<=1/(double)n;i+=DBL_MIN)//do something

          According to the C++ standard library reference cfloat, the value of the macro constant DBL_MIN is 10 - 37 or less.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            If we consider the input as n, when n → inf, this program runs for 0 times, which means its complexity is O(1)

            This is what my coach told me, I think it is also reasonable...

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
              ← Rev. 3   Vote: I like it 0 Vote: I do not like it

              Note that the increment δ i can theoretically be made arbitrarily small as n increases such that the number of iterations m is never 0, and that m is equal to the reciprocal of n × δ i. Both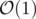 and 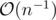expressions hide the actual value of δ i.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                6 years ago, # ^ |
                ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                Though the increment δ i could be made very small, n could be very large...

                So O(1) is still reasonable...I think.

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  6 years ago, # ^ |
                  ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                  If m is constant, and the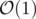 // do something execution time is fixed, then the time complexity is reasonable. Again, the time-complexity is only an asymptote that does not specify the actual execution time. It only describes briefly the rate of change of the execution time as the problem size or the input size increases.

                  → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +2 Vote: I do not like it

You should talk to babin. He's a master at least on this topic.

→ Reply