Hi there!
Consider the following problem: You're given set of n items with weights a1, ..., an. How many ways are there to select k items (order of choosing matters) with total weight of m (let's denote it as bm)? There are two main variants of the problem:
- You may take any item arbitrary number of times. In this case bm = [xm](xa1 + ... + xan)k.
- You may take each item exactly once. In this case bm = m...(1 + yxan)
First case is quite explicit and allows you to calculate answer in like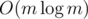 
as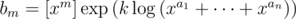 
.
But what about the second? If you define P(x) = xa1 + ... + xan and Qk(x) = b0 + b1x + b2x2 + ..., you may say for example that Q1(x) = P(x), Q2(x) = P2(x) - P(x2) or Q3(x) = P3(x) - 3P(x)P(x2) + 2P(x3) which allows to calculate Qk(x) for small k quickly. But does anybody know any fast way to calculate Qk(x)? Newton's identities seem to allow something like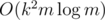 
if I'm not mistaken. Can anybody suggest any faster algorithm?
Hi, I've been studying polynomials and the FFT for about four days now (from various resources including CLRS, cp-algorithms, and an awesomely written work by you during the "Moscow International Workshop ACM ICPC 2017"). I've found out many fascinating applications, but I'm particularly intrigued by how polynomial multiplication can be used to solve some counting problems. For instance, in this problem, one is required to find the $$$K^{th}$$$ prefix sum of a sequence of length $$$N$$$. The way I solved it is as follows:
Assume the elements of the array, say $$$A\ = \ <a_0,\ a_1,\ \cdots,\ a_{n - 1}>$$$ are the co-efficients of a polynomial of degree-bound $$$N$$$ as:
Now we know:
What I found is that the coefficients of $P(x)^K$ correspond to the terms in the $$$K^{th}$$$ column in the Pascal's triangle, and we know that every subsequent column is the prefix sum of the previous. It lined up my solution, I just compute the first $$$N$$$ terms of $$$P(x)^K$$$ using NTT and Binary Exponentiation, and then multiplied the result by $$$F(X)$$$: the coefficients of the first $$$N$$$ terms of $$$P(x)^K.F(x)$$$ correspond to the $$$K^{th}$$$ prefix sum of $$$A$$$.
Motivated by this, I tried to find some resources about the topic but couldn't. And finally, I found this blog which seems like something I was looking for. Can you help me understand the intuition behind using the coefficients and the exponents of a polynomial in such problems? Also, can you elaborate on how these work:
And well, thank you! :)