sheaf's blog

[Timus 1766] How to apply Gaussian elimination?
By sheaf, history, 6 years ago, In English

Hello everyone. I've just solved Timus 1766. The solution has something to do with random walks and Markov chains (not going to describe it). The problem reduces to computing A∞v. I have solved it by raising a certain matrix A to sufficiently big power (2120 in my case). After reading problem discussions I've found out it could be computed using Gaussian elimination. Can anybody explain what does Gaussian elimination have to do with raising matrix to an infinite power?

  • Vote: I like it
  • -10
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

did you solve easier tasks about expected value (or probability) with infinite process? almost all solutions becomes to solve some equations

simpe example: expected value of toses coin to achive head (p = prob-ty to head, q=1-p):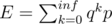

but we can do it another way: E = p + q(1 + E). with probability p we achive haed or, with q we go to the same start situation, so we need 1+E toses. and find E by solving equation

so, seems like in your task its system of equations, try to think

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A∞ = A∞ + 1 (wow, infinities)

So, A∞v = A(A∞v). Actually you are trying to find fixed point of f(x) = Ax. The problem can be that there are a lot of such fixed points and which of them will be a result of given process is not clear, but in this case everything is fine.

→ Reply